 |
Cells – Percentages – Total (по строкам и по столбцам)
|
|
|
|
Соотношения в таблицах сопряженности применимы только к выборке; для того, чтобы проверить, возможно ли распространить результаты на генеральную совокупность, необходимо использовать специальные критерии, описанные в Главе 2 и, в частности, вычислить критерий хи-квадрат Пирсона.

Рис. 3.10. Вычисление таблиц сопряженности

Рис. 3.11. К вычислению таблиц сопряженности
Нулевая гипотеза предполагает, что между переменными нет никакой зависимости. Используем пункты меню (рис.3.12):
Statistics – Summarize – Crosstabs - ……. ………-Statistics … - Chi-square
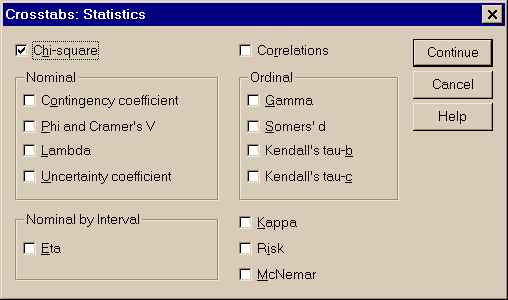
Рис. 3.12. Вычисление критерия хи-квадрат Пирсона
В таблицах окна вывода программы SPSS исследователь получает следующие результаты:
Pearson Chi-Square – хи-квадрат Пирсона.
Likelihood Ratio – отношение правдоподобия. Рассчитывается по более сложной формуле, чем хи-квадрат Пирсона (хи-квадрат представляет собой приблизительную оценку отношения правдоподобия).
Linear-by-Linear Association – критерий линейно-линейной зависимости. Представляет собой коэффициент корреляции, применим только если обе переменные – порядковые!
В таблице в окне вывода: Value – значения критерия, df - количество степеней свободы, Asymp.Sig.(2-sided)- уровень значимости (рис. 2.14 в Главе 2). Обычно нулевая гипотеза отвергается, если уровень значимости меньше 5% (0.05).
Для того, чтобы определить вклад каждой ячейки таблицы в общее значение критерия хи-квадрат, можно в меню:
Statistics – Summarize – Crosstabs - …….- Cells
выбрать для вывода также значения:
Expected – ожидаемое значение;
Unstandarized – ненормированные остатки;
Standarized – нормированные остатки
All Standarized – исправленные нормированные остатки (рис. 3.11).
Величины остатков позволяют судить о том, насколько сильно фактические значения отличаются от ожидаемых, или какие значения более всего отклоняются от нулевой гипотезы (если она верна, остатки должны быть равны нулю).
|
|
|
3.4. Вычисление корреляционных функций.
Как было показано в Главе 2, корреляция - это исследование комбинаций непрерывных переменных. Графическое представление зависимости между переменными можно получить с помощью диаграммы рассеяния. Для построения диаграммы рассеяния используются пункты меню:
Graphs – Scatter – Simple – Define – выбор переменных
Диаграмма позволяет на глаз оценить зависимость двух переменных.

Рис. 3.13. Построение диаграммы рассеяния
Поверх уже созданной диаграммы в окне вывода можно наложить линию наименьших квадратов. В окне Редактора графиков (чтобы его вызвать, необходимо два раза щелкнуть левой клавишей мыши на графике в окне вывода) требуется задать: Charts – Options – Fit Line – Total

Рис. 3.14. Наложение линии наименьших квадратов поверх диаграммы рассеяния
Если требуется обнаружить квадратичную или кубическую зависимость, необходимо в окне редактора графиков выбирать Fit Options.
Информацию о зависимости между переменными можно получить, вычислив коэффициент корреляции Пирсона r:
r = 1 – прямая зависимость;
r = -1 - обратная зависимость;
r = 0 - отсутствие зависимости (вернее, в данном случае линейную зависимость установить не удается и можно попытаться установить нелинейную зависимость, используя диаграммы рассеяния – см. выше). Для вычисления коэффициента корреляции Пирсона используются пункты меню:
Statistics – Correlate - Bivariate –
выбор переменных – Correlation Coefficients - Pearson

Рис. 3.15. Вычисление коэффициента корреляции Пирсона
Для каждой выбранной пары переменных принимается нулевая гипотеза о том, что линейная зависимость между ними отсутствует.
Результаты вычислений помещаются в таблицу Correlations в окне вывода (рис.2.11, Глава 2):
Pearson Correlation – коэффициент корреляции;
|
|
|
Sig. (2-tailed) – уровень значимости коэффициента;
N - количество записей в файле данных, по которым делался расчет.
Особое внимание следует обратить на уровень значимости – любая значимость выше 0.05 (5%) подтверждает нулевую гипотезу (о том, что в генеральной совокупности значение коэффициента корреляции равно нулю).
Для использования коэффициента корреляции Пирсона необходимо, чтобы все переменные были непрерывными и данные являлись бы случайной выборкой из генеральной совокупности с нормальным распределением. В том случае, когда какое-либо из этих условий не выполняется и коэффициент Пирсона использовать нельзя, применяются так называемые непараметрические критерии и, в частности, коэффициент ранговой корреляции Спирмена. Его значение также заключено между –1 и +1, интерпретация осуществляется так же, как и интерпретация значений коэффициента Пирсона.
Statistics – Correlate - Bivariate – выбор переменных —
— Correlation Coefficients - Spearman
Коэффициент Спирмена менее мощный, чем коэффициент Пирсона, поскольку в нем используется меньше информации о данных; тем не менее он является весьма полезным и часто используется в случае невозможности использования критерия Пирсона.
Как уже подчеркивалось в Главе 2, при интерпретации результатов исследования комбинации переменных с помощью корреляции, необходимо помнить, что сильная корреляционная зависимость между переменными совсем не означает, что одна является причиной другой!
3.5. Расчет t-критерия.
t–критерий применяется для сравнения двух групп, образованных категориями независимой переменной по характеристикам распределения зависимой непрерывной переменной.
В основе t-критерия лежат следующие предположения.
- Две группы являются взаимоисключающими, т.е. каждое наблюдение может попасть только в одну из этих групп.
- Данные получены в результате случайной выборки из генеральной совокупности с нормальным распределением непрерывной переменной.
- В генеральной совокупности в обеих группах одинаковая дисперсия непрерывной переменной
Как правило, перед расчетом t-критерия осуществляется проверка двух последних предположений. Для проверки равенства дисперсий используется критерий Ливиня (Levene test), который более устойчив к нарушению нормальности распределения, чем другие критерии; в программе SPSS он автоматически рассчитывается при расчете t-критерия. Нулевая гипотеза, которую проверяет критерий Ливиня – равенство внутригрупповых дисперсий.
|
|
|
Как и все виды генерализующей статистики, t-критерий используется для того, чтобы на основе данных нашей выборки оценить вероятность того, что обнаруженные различия являются подлинными (существующими в генеральной совокупности), а не вызваны исключительно случайной ошибкой выборки.
Нулевая гипотеза состоит в том, что средние значения исследуемой переменной в группах равны (применительно к обработке опросного листа - например, в группе мужчин и группе женщин).
Для расчета t-критерия используются пункты меню:
Statistics – Compare Means – Independent Samples T Test – — выбор переменных – для переменной Grouping Variable определить группы – Define Groups


Рис. 3.16. Формирование задания для вычисление t- критерия
Результаты вычислений в окне вывода находятся в таблице Group Statistics (рис.2.15, Глава 2):
Levene's Test for Equality of Variances – критерий равенства дисперсий Ливиня. Приводится значение критерия F и уровень его значимости Sig. Если уровень значимости критерия ниже 0.05, то нулевая гипотеза о равенстве дисперсий отвергается, и можно использовать только вторую строку таблицы – Equal variances not assumed (равенство дисперсий не предполагается). В противном случае используется первая строка.
t - значение t-критерия. Показывает направление и степень межгруппового различия средних.
Sig (2-tailed) – уровень значимости t-критерия. Если уровень значимости больше 0.05, принимается нулевая гипотеза о равенстве средних в подгруппах; в противном случае – отвергается.
В том случае, если данные не удовлетворяют требованиям t-критерия (например, невозможно установить, что групповые дисперсии равны), можно использовать непараметрические критерии. Наиболее подходящим непараметрическим критерием, заменяющим t-критерий, является критерий Манна-Уитни (обозначается буквой U). Для расчета значения критерия подгруппы ранжируются; нулевая гипотеза состоит в том, что суммы рангов в обеих группах должны быть равными, и рассчитываемый уровень вероятности показывает вероятность этой гипотезы.
|
|
|
Для расчета значения критерия применяются пункты меню (рис. 3.17): Statistics – Nonparametric Tests – 2 Independent Sample –
выбор переменных — Test Variable List, Grouping Variable Define Variable — Mann-Whitney U

Рис. 3.17. Вычисление критерия Манна-Уитни
Интерпретация результатов совершенно аналогична интерпретации результатов вычисления t-критерия. Если symp. Sig. (2-tailed) – рассчитанный уровень вероятности, - 0.05, то нет оснований отвергнуть нулевую гипотезу.
Хотя непараметрический критерий Манна-Уитни менее мощный, чем t-критерий, поскольку он использует меньше информации о данных, этот критерий часто используется в тех случаях, когда нет уверенности в том, что данные соответствуют условиям применимости t-критерия.
3.6. Регрессионный анализ.
Линейный регрессионный анализ позволяет получить предсказание значений зависимой переменной на основе значений независимых переменных.
Линейный регрессионный анализ является достаточно сложной статистической процедурой. Поэтому здесь ограничимся рассмотрением случая одной зависимой и одной независимой переменной и будем использовать процедуру простой линейной регрессии.
Для расчета линейной модели регрессии необходимо использовать пункты меню (рис. 3.18):
Statistics – Regression - Linear –
выбрать переменную и поместить ее в окно Dependent (зависимая переменная) – выбрать переменную и поместить ее в окно Independet(s) (независимые переменные).
Нажав кнопку Statistics… можно задать расчет ряда коэффициентов регрессии, нажав кнопку Plots… - вид выводимых графиков в процедуре линейной регрессии (рис. 3.19), можно задать сохранение результатов процедуры "Линейная регрессия" (кнопка Save…) и параметры процедуры регрессии (кнопка Options…)

Рис. 3.18. Вычисление регрессионной модели
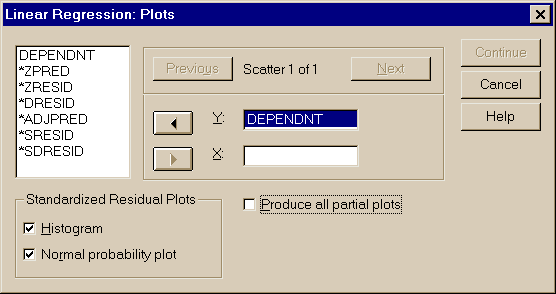
Рис. 3.19. Задание на расчет коэффициентов регрессии и вида графиков
При интерпретации результатов, полученных в окне вывода программы SPSS, необходимо учитывать, что некоторые выходные данные требуются только при построении сложных регрессионных моделей. Поэтому рассмотрим только основные элементы выходных данных (рис. 2.19, Глава 2).
В сноске к таблице Model Summary дается информация, которая показывает, насколько хорошо можно представить значение зависимой переменной на основе независимой:
R – коэффициент корреляции между переменными;
R-square - квадрат коэффициента корреляции (показывает, какая часть изменчивости зависимой переменной может быть объяснена независимой переменной).
|
|
|
При интерпретации выходных данных необходимо учитывать значимость коэффициентов (столбец Sig. таблицы ANOVA): линейная регрессионная модель зависимости является надежной, если уровень значимости не превышает 0.05 (5%).
В таблице Coefficients (коэффициенты) приводятся рассчитанные коэффициенты регрессионной модели: регрессионный коэффициент (тангенс угла наклона прямой), а также постоянная прямой. Значение в первой строке столбца В таблицы (Constant) – постоянная, во второй (где приведено имя переменной) – коэффициент (тангенс угла наклона прямой). С помощью этих чисел можно записать уравнение прямой:
Зависимая переменная = Коэффициент * Независимая
переменная + Постоянная
Теперь, используя это уравнение, можно по заданному значению независимой переменной вычислять значения (предсказанные) зависимой переменной.
В столбце Sig. таблицы Coefficients представлен уровень значимости для каждого регрессионного коэффициента. При 5%-ном уровне значимости можно считать неравными нулю только те коэффициенты, для которых значение Sig. не превышает 0.05.
3.7. Редактирование таблиц и графиков в окне Навигатора
Вывода.
Результаты выполнения процедур SPSS выводятся в окно, называемое Output Navigator (Навигатор Вывода). Непосредственно в окне Навигатора можно отредактировать выводимые результаты и создать документ, содержащий именно то, что необходимо исследователю для создания полноценного отчета о результатах анализа опросных листов.
Навигатор вывода можно использовать для того, чтобы:
- просматривать выводимые данные;
- показывать или скрывать выбранные таблицы и диаграммы;
- изменять порядок следования элементов вывода;
- переходить к Редактору Таблиц, Редактору Текста или Редактору Диаграмм;
- перемещать объекты SPSS в другие приложения (например, документ текстового редактора Word).
Окно навигатора (рис. 3.20) разделено на две части - в левой находится схема вывода, в правой - сами результаты (статистические таблицы, диаграммы, текст). Пользователь может передвигать границу между этими частями, если он захочет изменить ширину левой или правой части.
Содержимое окна Навигатора может быть сохранено в документе во внутреннем формате SPSS - *.spo, для чего необходимо использовать:
File - Save (Save As …),
а для сохранения вывода во внешних форматах (текстовом, HTML), использовать:
File - Export - Тип файла
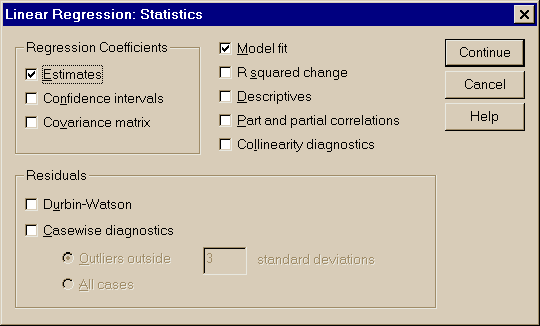
Рис. 3.20. Окно навигатора вывода
Для того, чтобы скрыть таблицу или диаграмму, не удаляя их, необходимо щелкнуть дважды на пиктограмме, изображающей открытую книгу, в левой части Навигатора Вывода, либо выбрать в меню: View - Hide.
Перемещение, копирование и удаление результатов можно производить либо с помощью мыши, перетаскивая при нажатой левой клавише нужные элементы в левой часто окна навигатора, либо используя элементы меню:
|
|
|


