Кинематика точки. Введение в кинематику.

Лекция 1. Кинематика точки и твердого тела.

В данной лекции рассматриваются следующие вопросы:

1. Краткие сведения по истории развития кинематики.

2. Кинематика точки. Введение в кинематику.

3. Способы задания движения точки.

4. Вектор скорости точки.

5. Вектор ускорения точки.

6. Определение скорости и ускорения точки при координатном способе задания движения точки.

7. Касательное и нормальное ускорение точки.

9. Некоторые частные случаи движения точки.

 

Краткие сведения по истории развития кинематики

Кинематика, как специальный раздел теоретической механики, возникла позднее статики и динамики, а именно, в начале второй половины XIX в. Появление первых исследований по кинематике связано с изобретением огнестрельного оружия. В первую очередь внимание исследователей привлекали вопросы определения траекто­рии полета снаряда, уточнение понятий о неравномерном и криво­линейном движении точки. Леонардо да Винчи (1452—1519) первый экспериментально изучал вопрос о свободном вертикальном паде­нии тяжелого тела. Однако лишь благодаря трудам Г. Галилея (1564—1642) развитие механики тесно связывается с запросами техники того времени. Галилею принадлежит введение понятия об ускорении и доказательство того, что траекторией движения снаряда, брошенного в пустоте под некоторым углом к горизонту, является парабола. Законы, найденные Галилеем, были развиты в исследова­ниях Э. Торричелли (1608—1647), установившем формулу пропорцио­нальности скорости падения тела корню квадратному из высоты падения. Обобщение понятия ускорения на случай криволинейного движения было получено X. Гюйгенсом (1629—1695), который первым обратил внимание на возможность разложения ускорения при криволинейном движении на касательное и нормальное. Однако строгое доказательство этого было дано Л. Эйлером (1707—1783).

Кинематические законы движения планет были установлены И. Кеплером (1571—1630). Эти законы легли в основу закона все­мирного тяготения, открытого Ньютоном.

Л. Эйлеру принадлежат основополагающие исследования по ки­нематике точки в случае естественного способа задания движения, по кинематике вращательного движения твердого тела вокруг непо­движной точки. Он создал широко применяемый метод кинематиче­ского описания движения твердого тела с помощью трех углов, назы­ваемых углами Эйлера.

Развитие кинематики системы обязано трудам Ж. Лагранжа (1736-1813).

Однако только бурный рост машиностроения в XIX в. повлек за собой расцвет кинематики как науки. По предложению Ж. Ампе­ра в 1851 г. кинематика выделилась в особый раздел теоретической механики. Появляется ряд глубоких исследований по кинематике твердого тела французских ученых М. Шаля (1793—1886), Л. Пуансо, Г. Кориолиса (1792—1843). П. Л. Чебышев (1821—1894) создал в России научную школу по кинематике механизмов. Богатое науч­ное наследие по кинематике механизмов Чебышева разрабатывается советскими учеными, среди которых, в первую очередь, следует отметить Н. И. Мерцалова (1860—1948), И. И. Артоболевского, А. П. Котельникова (1865—1940), Д. С. Зернова, Л. В. Асура (1878—1920), Я. Л. Геронимуса и др.

«Отцу русской авиации» Н. Е. Жуковскому (1847—1921) принад­лежат первоклассные работы по теоретической механике, в том числе и по кинематике, в которых широко внедрены геометрические методы доказательств различных теорем. Ряд замечательных иссле­дований по кинематике принадлежит профессору Одесского уни­верситета В. Н. Лигнину (1846—1900), возглавлявшему на Украине научное направление исследований по кинематике.

 

Кинематика точки. Введение в кинематику.

Кинематикой (от греческого «кинема» — движение) называется раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил.

Основной задачей кинематики является нахождение положения тела в любой момент времени, если известны его начальное положение, скорость и ускорение в начальный момент времени.

Механическое движение - это изменение положения тел (или частей тела) относительно друг друга в пространстве с течением времени.

Для определения положения движущегося тела (или точки) в разные моменты времени с телом жестко связывают систему отсчета.

Тело отсчета - тело (или группа тел), принимаемое в данном случае за неподвижное, относительно которого рассматривается движение других тел.

Система отсчета - это система координат, связанная с телом отсчета, и счетчик времени.

Положение тела можно определить с помощью радиус-вектора или с помощью координат.

Радиус-вектор точки М - направленный отрезок прямой, соединяющий начало отсчета О с точкой М.

Координата точки М - это проекция конца радиуса-вектора точки М на ось. Обычно пользуются прямоугольной системой координат Декарта. В этом случае положение точки М на линии, плоскости и в пространстве определяют соответственно одним (х), двумя (х, у) и тремя (х, у, z) числами - координатами.

 

Материальная точка - тело, размерами которого в данных условиях можно пренебречь.

Этой моделью пользуются в тех случаях, когда линейные размеры рассматриваемых тел много меньше всех прочих расстояний в данной задаче или когда тело движется поступательно.

Основной задачей кинематики точки является изучение законов движения точки. Зависимость между произвольными положениями движущейся точки в пространстве и времени определяет закон ее движения. Закон движения точки считают известным, если можно определить положение точки в пространстве в произвольный момент времени.

Поступательным называется движение тела при котором все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорения. Поэтому для описания такого движения тела достаточно описать движение его одной произвольной точки.

В дальнейшем под словом "тело" будем понимать "материальная точка".

Линия вдоль которой движется тело называется траекторией. На практике форму траектории задают с помощью математических формул (у=f(х) — уравнение траектории) или изображают на рисунке. Вид траектории зависит от выбора системы отсчета.

В зависимости от вида траектории различают прямолинейное и криволинейное движение.

Путь s – длина траектории.

Перемещение тела - вектор соединяющий начальное (точка М₀) и конечное (точка М) положение тела:

, где и 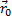— радиус-векторы тела в эти моменты времени.

Проекция перемещения на ось Ох: ∆r_x =∆х = х-х₀, где x₀ и x - координаты тела в начальный и конечный моменты времени.

Модуль перемещения не может быть больше пути: 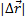≤s.

Зная перемещение и начальное положение тела, можно найти его положение в момент времени t:

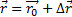
Скорость – векторная величина численно равная расстоянию пройденного телом за единицу времени.

Единица измерения скорости – м/с. Часто используют и другие единицы, например, км/ч: 1 км/час=1/3,6 м/с.

 

Поделиться:

Воспользуйтесь поиском по сайту: