Часть 3. Обработка многократных измерений

Содержание

Часть 1. Расчет полей допусков размеров детали. 3

Часть 2. Расчет сборочных размерных цепей методами взаимозаменяемости. 8

Часть 3. Обработка многократных измерений. 19

Список литературы: 24

Часть 1. Расчет полей допусков размеров детали.

 

 

Задание.

Рассчитать параметры посадки Æ40 ; написать все виды обозначения предельных отклонений размеров на конструкторских и рабочих чертежах.

Для расчета дана посадка с зазором в системе отверстия.

1.Отклонения отверстия и вала по ГОСТ 25347-82:

 

Схема расположения полей допусков посадки

 

2.Предельные размеры:

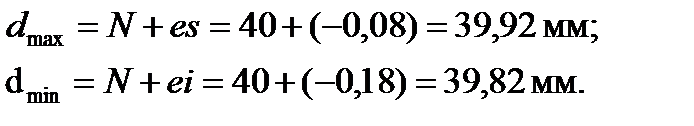
3.Допуски отверстия и вала:

либо

4.Зазор:

либо

5.Средний зазор:

6.Допуск посадки с зазором:

Обозначение предельных отклонений размеров на конструкторских чертежах:

 

 

 

 

а) условное обозначение полей допусков:

б) числовые обозначения предельных отклонений:

в) условное обозначение допусков и числовых значений предельных отклонений:

8.Обозначение размеров на рабочих чертежах:

 

Часть 2. Расчет сборочных размерных цепей методами взаимозаменяемости.

 

Задача №1.1

Назначить допуски и отклонения составляющих размеров с таким расчетом, чтобы обеспечить значение замыкающего размера, равное мм. Расчет произвести методом полной взаимозаменяемости.

На детали, входящие в сборочный комплект, назначены следующие значения номинальных размеров:

N_A1=19 мм; N_A2=136 мм; N_A3=19 мм; N_A4=188 мм; N_A5=3 мм; N_A6=16 мм.

1.Согласно заданию имеем

;

;

;

;

.

2.Составим график размерной цепи:

 

3.Составим график размерной цепи:

(1)

Значения передаточных отношений

Обозначение передаточных отношений	x1	x2	x3	x4	x5	x6
Численное значение xj	-1	-1	-1	+1	+1	-1

4.Произведем проверку правильности назначения номинальных значений составляющих размеров:

Т.к. по условию задачи N_D=1, следовательно, номинальные размеры назначены правильно.

5. Осуществим увязку допусков, для чего из величины T_D рассчитаем допуски составляющих размеров.

Т.к. в узел входят стандартные изделия (подшипники), допуски которых являются заданными, то для определения величины a_c воспользуемся зависимостью:

(2)

 

где T_D - допуск замыкающего размера, мкм;

i_j – значение единицы допуска, мкм.

6.По таблице допусков для размеров до 500 мм по ГОСТ 25346 – 82 устанавливаем, что такому значению a_c соответствует точность, лежащая между 11 и 12 квалитетами. Примем для всех размеров 11 квалитет. Точность

5%, тогда:

T₂=0,25мм; T₄=0,29 мм; T₅=0,06 мм; T₆=0,11; T₁=T₃=0,12.

7.Произведем проверку правильности назначения допусков составляющих размеров по уравнению

(4)

где T_D и T_j – допуски замыкающего и j-го составляющего размеров.

8.Осуществим увязку средних отклонений, для чего примем следующий характер расположения полей допусков составляющих размеров.

A₁=A3=19 (_-0,12) мм;

A₂=136h11(_-0,250) мм;

A₄= 188JS11( 0,145) мм;

A₅= 3h11 (_-0,6) мм;

A₆= 16JS11 (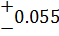) мм;

 

Сведем данные для расчета в таблицу:

Обозначение размера	Размер	xj	Ecj	xjEcj
A1	19 (-0,12)	-1	-0.06	0.06
A2	136h11(-0,250)	-1	-0.125	0.125
A3	19 (-0,12)	-1	-0.06	0.06
A4	188JS11( 0,145)	+1
A5	3h11 (-0,6)	+1	-0.03	0.03
A6	16JS11 (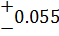)	-1

 

По уравнению:

(5)

найдем среднее отклонение замыкающего размера и сравним его с заданным

 

Предельные отклонения А₂:

;

;

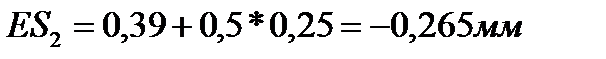Таким образом .

 

 

Задача №1.2(обратная)

Найти предельные значения замыкающего размера A_D при значениях составляющих размеров, полученных в результате решения задачи №1.1. Расчет произвести методом полной взаимозаменяемости.

Сведем данные для расчета в таблицу

Обозначение размера	Размер	xj	Nj	Ecj	Tj	xjNj	xjEcj	çxjêTj
A1	19 (-0,12)	-1		-0,06	0,12	-19	+0,06	+0,12
A2	136h11	-1		-0.125	0,25	-136	+0.125	+0,25
A3	19 (-0,12)	-1		-0,06	0,32	-19	+0,06	+0,32
A4	188JS11( 0,145)	+1			0,29	+188		+0,29
A5	3h11 (-0,6)	+1		-0.03	0,06	+3	-0,03	+0,06
A6	16JS11 (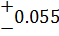)	-1			0,11	-16		+0,11

 

1.Номинальное значение замыкающего размера

.

2.Среднее отклонение замыкающего размера

.

3.Допуск замыкающего размера

.

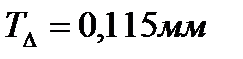4.Предельные отклонения замыкающего размера

;

.

5.Сравним полученные результаты с заданными

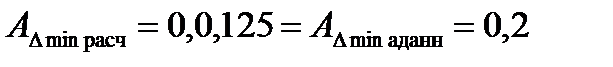
Т.к. условие:

(6)

выполняется, следовательно, изменения предельных отклонений составляющих размеров не требуется.

Задача №2.1.

Назначить допуски и отклонения составляющих размеров с таким расчетом, чтобы обеспечить значение замыкающего размера, равное . Расчет провести вероятностным методом, исходя из допустимого процента брака на сборке, равного 0,27%.

На детали, входящие в сборочный комплект, назначены следующие значения номинальных размеров:

N_A1=19 мм; N_A2=136 мм; N_A3=19 мм; N_A4=188 мм; N_A5=3 мм; N_A6=16мм.

1.Согласно заданию имеем

;

;

;

;

.

 

2.Составим график размерной цепи:

 

3.Составим график размерной цепи:

(1)

Значения передаточных отношений

Обозначение передаточных отношений	x1	x2	x3	x4	x5	x6
Численное значение xj	-1	-1	-1	+1	+1	-1

4.Произведем проверку правильности назначения номинальных значений составляющих размеров:

Т.к. по условию задачи N_D=1, следовательно, номинальные размеры назначены правильно.

5. Осуществим увязку допусков, для чего из величины T_D рассчитаем допуски составляющих размеров.

Т.к. в узел не входят стандартные изделия (подшипники), то для определения величины a_c воспользуемся зависимостью:

(7)

Подставляя численные значения получим:

6.По таблице допусков для размеров до 250 мм по ГОСТ 25346 – 82 устанавливаем, что такому значению a_c больше принятого для квалитета 13, но меньше, чем для квалитета 14.Установим для всех размеров допуски по 13 квалитету, тогда:

T₁=T3=0,12 мм, T₂=0,63 мм, T₄= 0,72 мм, T₅=0,14 мм, T6=0,27 мм.

7.Произведем проверку правильности назначения допусков составляющих размеров по уравнению:

(8)

где T_D и T_j – допуски замыкающего и j-го составляющего размеров;

λ_D и λ_j – относительные средние квадратические отклонения законов распределения значений замыкающего и j-го составляющего размеров.

λ_D=0.333(т.к. допустимое количество брака на сборке равно 0.27%);

λ_j=0.4 – для всех видов размеров.

.

Полученная сумма допусков меньше заданного. Для того, чтобы полностью использовать заданный допуск замыкающего размера, расширим допуск размера А₂ и найдем его из уравнения (8):

 

 

 

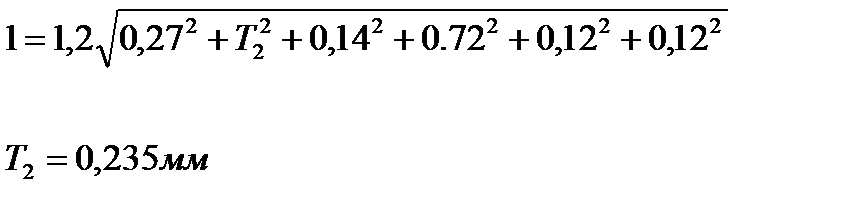
8.Осуществим увязку средних отклонений. Увязку будем производить за счет среднего отклонения размера А₂,принятого в качестве увязочного.

Примем следующий характер расположения полей допусков составляющих размеров.

 

A₆=16JS13() мм;

A1=A₃=19(_-0.12) мм;

A₄=188JS13(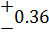) мм;

A₅=3h13(_-0.14) мм.

Сведем данные для расчета в таблицу:

Обозначе-ние размера	Размер	xj	Ecj	Tj	aj
A1	19(-0.12)	-1	-0.06	0,12	+0,2	0,012	-0,048	+0,048
A2		-1	Ec2	0,63	+0,2	0,063	Ec2+0,063	-(Ec2+0,04)
A3	19(-0.12)	-1	-0.06	0,12	+0,2	0,012	-0,042	+0,042
A4	188JS13(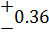)	+1		0,72
A5	3h13(-0.14)	+1	0,07	0,14	+0,2	0,014	-0,084	0.084
A6	16JS13()	-1		0,24

(9)

 

По уравнению (9) найдем среднее отклонение размера A₂:

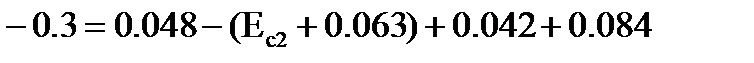
Предельные отклонения размера A₂:

Таким образом

Задача №2.2(обратная)

Найти предельные значения замыкающего размера A_D при значениях составляющих размеров, полученных в результате решения задачи №2.1. Расчет произвести вероятностным методом, исходя из допустимого процента брака на сборке, равного 0,27%.

Сведем данные для расчета в таблицу

Обозна-чение размера	Размер	xj	Ecj	Tj	aj
A1	19(-0.12)	-1	-0,06	0,12	+0,2	0,012	-0,0048	+0.048	0,12	0,0144
A2		-1	Ec2	0,235	+0,2	0,0235	+0,4345	-0.4345	0,4345	0,188
A3	19(-0.12)	-1	-0,06	0,12	+0,2	0,012	-0,042	+0.042	0,12	0,0144
A4	188JS13(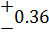)	+1		0,72					0,72	0,5184
A5	3h13(-0.14)	+1	-0,07	0,14	+0,2	0,014	+0.084	+0.084	0,14	0,0196
A6	16JS13()	-1		0,27					0.27	0,0729

 

1.Номинальное значение замыкающего размера:

 

2.Среднее отклонение замыкающего размера (по формуле 9):

3.Допуск замыкающего размера

(10)

4.Предельные отклонения замыкающего размера

мм;

мм.

 

5.Сравним полученные результаты с заданными

Т.к. условие:

(6)

выполняется, следовательно, изменения предельных отклонений составляющих размеров не требуется.

 

Часть 3. Обработка многократных измерений

Задание

Определить вид ЗРВ по критерию Пирсона;

Записать результат с доверительной вероятностью P=0.95. ∑строки

32,60 32,64 32,60 32,48 32,57 32,50 32,44 32,85 32,59 32,66 32,68 32,50 32,47 32,50 456,08 32,53 32,54 32,68 32,45 32,58 32,49 32,47 32,67 32,66 32,65 32,71 32,76 32,66 32,58 456,43 32,68 32,57 32,56 32,64 32,55 32,53 32,43 32,70 32,50 32,65 32,67 32,54 32,55 32,61 456,18 32,66 32,58 32,70 32,72 32,60 32,66 32,57 32,71 32,55 32,59 32,55 32,63 32,72 32,56 456,80 32,66 32,54 32,57 32,57 32,63 32,64 32,49 32,54 32,67 32,73 32,59 32,51 32,61 32,60 456,35 32,52 32,67 32,62 32,50 32,58 32,66 32,65 32,66 32,69 32,53 32,58 32,61 32,77 32,63 456,67 32,52 32,62 32,70 32,67 32,56 32,61 32,47 32,54 32,42 32,59 32,63 32,70 32,60 32,50 456,13 32,62 32,63                         65,25                             3259,89

32,6 32,53 32,68 32,66 32,62 32,64 32,54 32,57 32,58 32,67 32,63                       32,56 32,70 32,72 3,48 32,45 32,55 32,50 32,49 32,61 32,44 32,47                       32,43 32,65 32,85 32,71 32,59 32,69 32,42 32,73 32,76 32,51 32,77                       32,52

 

 

1.Определяем среднее арифметическое и стандартное отклонение для данных таблицы:

2.С помощью правила «трех сигм» проверяем наличие или отсутствие промахов.

Таким образом, ни один из результатов не выходит за границы интервала [ ], следовательно, с вероятностью 0.9973 гипотеза об отсутствии грубых погрешностей принимается.

3.Построение гистограммы и выдвижение гипотезы о виде закона распределения вероятности.

Участок оси абсцисс, на котором располагается вариационный ряд значений физической величины, разобьем на k одинаковых интервалов .

Принимая k=7, получим

Результаты производимых вычислений занесем в первую половину таблицы 1, и строим гистограмму.

 

Из вида гистограммы можно сделать предположение о том, что вероятность результата измерения подчиняется нормальному закону. Проверим правдивость этой гипотезы.

Таблица 1

i	Интервалы	mi				Фi-1	Фi	Pi
xi-1	xi
	32,4	32,45			-2,459	-1,229	-0.9861	-0.7813	0,2048	5,302
	32,45	32,5
	32,5	32,55		3,4	-1,229	-0,614	-0.7813	-0.4581	0,3232	7,242
	32,55	32,6		4,2	-0,614		-0.4581		0,4581	13,43
	32,6	32,65				0,614		0.4581	0,4581	14,54
	32,65	32,7			0,614	1,229	0.4581	0.7813	0,3232	4,69
	32,7	32,75		0,8	1,229	3,073	0.1819	0.9978	0,1788	5,83
	32,75	32,8
	32,8	32,89

4.Проверка нормальности закона распределения по критерию Пирсона.

Т.к. в предыдущем пункте выдвинута гипотеза о нормальности распределения, то для расчета вероятностей используем функцию Лапласа:

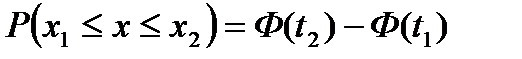
В данном случае значения x₁ и x₂ соответствуют началу и концу интервала. Для каждого из значений нужно рассчитать относительный доверительный интервал , а затем из таблиц функции Лапласа находим соответствующие значения этой функции Ф(t₁) Ф(t₂).

Найдя, таким образом, значения P_i для каждого интервала k_i, заполним соответствующие ячейки таблицы 1, а затем рассчитаем значение c² – критерия для каждого интервала.

Суммарное значение c²:

Определим табличное (критическое) значение c², задавшись доверительной вероятностью 0.94 и вычислив по формуле r=k-3 число степеней свободы:

r=7-3=4

Таким образом, с вероятностью 0.95 гипотеза о нормальности распределения вероятности результата измерения принимается.

Поделиться:

Воспользуйтесь поиском по сайту: