Напряженное состояние пород в районе горных выработок

 

Призабойная зона скважин представляет собой область пласта, от характеристики которого зависит производительность скважин. Эта область самого узкого сечения потока в процессе вскрытия пласта и эксплуатации скважин подвержена воздействию раствора воды, цемента, отложения парафина, солей и смол, заиливания и т.д., в результате чего уменьшается приток нефти и газа. Поэтому свойствам пород призабойной зоны и процессам, происходящим в этой области, уделяется особое внимание.

С бурением скважины изменяется начальное напряженное состояние пород, так как происходят возмущения в естественном поле напряжений. В глубине пластов породы всесторонне сжаты, а по мере приближения к скважине они будут находиться в условиях, близких к одноосному сжатию. В результате пластичные породы (некоторые глины и глинистые сланцы) частично выдавливаются в скважину и удаляются в процессе бурения. В результате вертикальное горное давление на породы нефтяного пласта в районе скважины оказывается частично уменьшенным. При этом в простом естественном поле напряжений появляется зона аномалий. В горном деле установлено, что область аномалий, имеющая практическое значение, невелика; она только в несколько раз превосходит размеры горной выработки. Вместе с тем в этой области происходят существенные изменения условий залегания горных пород, которые могут быть причиной значительных изменений их фильтрационных свойств.

В простейшем случае (если рассматривать призабойную зону, как однородный упругий толстостенный сосуд) поиски распределения напряжений в этой зоне можно свести к решению задачи Ламе (рис. 3).

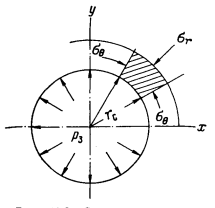
Рис. 3 - Схема распределения действующих напряжений в элементе породы призабойной зоны скважин

 

Как известно, напряжение в толстостенном цилиндре, сечения которого образованы концентрическими окружностями, подверженном действию равномерно распределенных сил, определяется соотношениями

 

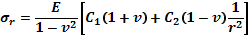
где 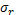  - радиальная компонента нормального напряжения;

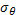 - окружное или тангенциальное нормальное напряжение;

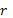 - расстояние от оси;

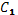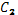 и  - постоянные интегрирования, которые можно определить из граничных условий:

при ;  (забойному давлению);

при 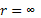; (горному давлению).

Для упрощения формулы запишем с другими постоянными в виде

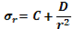
По этим формулам можно вычислить окружные и радиальные напряжения на разных расстояниях г от оси скважины.

Из граничных условий найдем

При , то

 

При , то

 

 

Следовательно

 

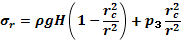
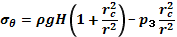
Из формул следует:

При , то

т. е. на стенке скважины могут действовать окружные сжимающие напряжения, величина которых при р3 =0 достигает двойного значения горного давления. Это означает, что при наличии пород недостаточной прочности в призабойной зоне возможно их разрушение под действием тангенциальных напряжений и ухудшение фильтрационных свойств пород вследствие их сжатия под влиянием этих нагрузок. Область аномалий, имеющая практическое значение, невелика; она лишь в несколько раз превосходит размеры горной выработки. Но последствия от нарушения скважиной начального поля напряжений могут существенно влиять на качество скважины и показатели ее работы в целом или отдельных участков продуктивного пласта.

Особо сложный характер распределение напряжений в зоне выработки имеет при неоднородных свойствах пород и наличии в разрезе пропластков, подверженных пластическим деформациям. В процессе бурения скважин пластические породы разреза способны частично "вытекать" в скважину и удаляться из нее, что сопровождается уменьшением вертикальных напряжений, которые в зоне возникновения пластических деформаций ниже вертикального горного давления. Радиус области разгрузки горного давления r_p вследствие пластической деформации пород определяется формулой

 

,

 

где r _п и r _в - плотности пород и воды; r_c - радиус скважины; Н - глубина скважины; К_п - коэффициент пластичности породы.

Например, при Н = 1500 м, К_п = 30,0 • 10⁵ Па, r _п = 2500 кг/м³, r _в = 1000 кг/м³; r_c = 0,15м радиус области разгрузки горного давления составит r _р = 4 м.

Очень часто давления разрыва пластов при их гидроразрыве оказываются меньше вертикального горного, что, вероятно, объясняется появлением зоны разгрузки в призабойной зоне скважин в связи с пластической деформацией пород некоторых пропластков.

На напряженное состояние пород и деформацию существенно влияют физико-механические свойства обсадных труб и цементного кольца, геометрия перфорационных каналов и депрессия давления, возникающая при эксплуатации скважин.

5. ОСОБЕННОСТИ РАСПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ В ПРИЗАБОЙНОЙ ЧАСТИ ВЫРАБОТКИ

 

Устойчивость горных выработок, особенно проводимых в сложных горно-геологических условиях, в первую очередь зависит от достоверности прогнозирования проявлений горного давления в начальный момент их существования, т.е. до вступления крепи во взаимодействие с породным обнажением. Адекватное отображение состояния породного массива в зоне влияния забоя выработки при её проведении можно получить лишь при учете перераспределения исходного поля напряжений, обусловленного образованием полости. В этом случае описание геомеханических процессов возможно только с использованием трехмерной модели, так как условие плоской деформации вблизи забоя выработки выполняется. Однако решение объемной численной задачи отличается значительными сложностями из-за трудоемкости конструирования сети конечных элементов, роста времени вычислений и усложнения обработки и корректировки результатов математического моделирования, и поэтому оно не пригодно для использования при оперативном прогнозировании геомеханических процессов.

С достаточной для практики точностью воспроизвести процессы деформировния и разрушения породного массива в призабойной части выработки можно путем замены пространственной задачи о формировании зоны разрушения вокруг выработки рядом последовательно решаемых плоских, когда начальные и граничные условия на каждом последующем шаге задаются исходя из решения задачи на предыдущем шаге. Однако при этом возникает необходимость в корректировке граничных условий, чтобы обеспечить соответствие между проявлениями горного давления, получаемыми из решения псевдопространственной задачи, и проявлениями, которые реализуются при объемной расчетной схеме.

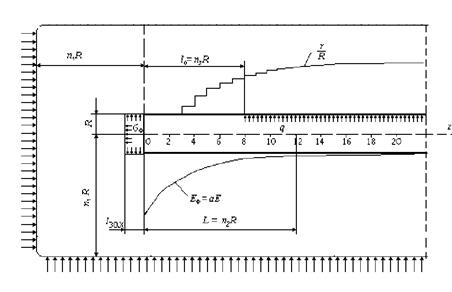
Рисунок 4 - Расчетная схема фрагмента массива вблизи забоя выработки на внутреннем контуре выработки

 

Расчетная схема фрагмента массива вблизи забоя горной выработки приведена на рис. 4, где граничные условия для напряжений записываются следующим образом:

 

σ_r = 0 при r = R и x < l₀ = n₃ x R;

σ_r = q при x > l₀;(1)

σ_x = 0 при 0 ≤ r ≤ R и x = 0;

 

в глубине породного массива -

 

σ_z = P при n₁ • R ≥ z ≥ -n₁ x R и x ≥n₁ • R;

σy = λ•P при n₁ • R ≥ z ≥ -n₁ • R и x ≥n₁ • R; (2)

σ_x = λ•P при x ≤ n₁ • R,

 

где q - отпор крепи;

l₀ - расстояние от забоя выработки до массива, где начинается силовое взаимодействие крепи с породным обнажением;

n₁, n₂, n₃ - целые числа, указывающие на кратность радиусу выработки R.

Главная особенность построения плоской численной модели в зоне влияния забоя выработки состоит в имитации изменчивости начального поля напряжений. Эти изменения обусловлены тем, что напряжения, воспринимавшиеся породой в пределах будущей полости, перераспределяются в глубину массива. Это перераспределение происходит не мгновенно, а постепенно (при буровзрывной технологии скачкообразно) в некоторой области, называемой обычно зоной влияния забоя, и характеризуются протяженностью. В пределах этой зоны условие плоской деформации ε_x = 0 не соблюдается, поэтому поле напряжений является переменным и может быть представлено в виде безразмерной функции f(L / R) от расстояния до забоя и времени существования выработки.

Исследовано три способа имитации перераспределения исходного поля напряжений.

В первом случае для учета влияния забоя к контуру выработки на участке 0 ≤ x ≤ L прикладывались фиктивные напряжения σ_ф, равные при x = 0 «снимаемым» напряжением по И.В. Родину, но противоположные по знаку, и постепенно снижающиеся до нуля на расстоянии x = L от забоя выработки. Однако имитация переменного поля напряжений в призабойной части выработки путем задания фиктивной радиальной нагрузки на поверхности полости нарушает граничные условия σ_r = 0 при x < l₀ и предполагает знание распределения напряжений по периметру будущей выработки, которые зависят от многих факторов, в том числе от неизвестного коэффициента бокового распора.

Второй способ состоял в заполнении выработки фиктивным материалом, модуль деформации Е_ф которого определялся по отношению к модулю упругости ненарушенной породы из выражения:

Eф =α E ^, (3)

 

где α - функция, задающая закон изменения поля напряжений в призабойной части выработки и зависящая от формы и размеров поперечного сечения, исходного поля напряжений, прочности пород и технологии горнопроходческих работ.

Для выработки круглого поперечного сечения функция а была принята в виде экспоненциальной зависимости:

 

а = e ^–Z/mR,(4)

 

где m - параметр аппроксимации.

При n₂ = 12 параметр m = 2, т.е. на расстоянии x =12R от забоя модуль Е_ф практически равен нулю, а граничные условия близки к плоской деформации. Однако выработки сооружаются, как правило, в неоднородном и анизотропном массиве, поэтому их модуль упругости не постоянная величина. Кроме того, в данном случае также нарушается граничное условие при x < l₀.

В условиях неопределенности исходного поля напряжений наиболее приемлемым способом моделирования геомеханических процессов в зоне влияния забоя выработки является применение на внешней поверхности модели фиктивной нагрузки, определяемой как:

 

Р_ф = f ( L/R)• P,(5)

 

где P_ф - фиктивная компонента напряжений, прикладываемая на контуре расчетной области на расстоянии x ≤ |L| от забоя.

При x ≥|L| параметр f (L/R)=1i, т.е. деформирование и разрушение пород происходит в постоянном поле напряжений; при x < -L, т.е. впереди забоя, параметр f (L/R)>1; при x < L, т.е. позади забоя, параметр f (L/R)<1i. Следовательно, при таком подходе не соблюдается граничное условие на внешней поверхности модели (2). Однако, учитывая то, что до сих пор в геомеханике исходное напряженное состояние массива задается на основании той или иной гипотезы, данное допущение не ведет к увеличению числа степеней свободы системы и не вносит существенных искажений в общую картину зарождения и формирования зон разрушения вокруг выработки. Более того, увязка результатов расчета с данными шахтных замеров путем корректировки параметра f (L/R) дает возможность использовать плоскую упругую пластическую модель в призабойной части выработки.Установление вида функции влияния забоя на напряженное состояние пород осуществлялось путем анализа пространственного распределения напряжений вокруг забоя выработок круглого и квадратного поперечного сечения, полученного с помощью математического моделирования на ПЭВМ методом конечных элементов. Расчетные схемы для решения задачи приведены на рис. 5. Упругий и невесомый фрагмент породного массива для воспроизведения поля напряжений нагружали за пределами зоны влияния выработки внешней нагрузкой, имитирующей действие отброшенных пород. Ввиду наличия двух плоскостей симметрии, моделировалась четверть исследуемой области, причем начало общей системы кординат (x, y, z) помещено в плоскости забоя выработки, а ось x совмещена с ее продольной осью (рис. 5). Конечно-элементная структура численной модели для выработки круглого поперечного сечения сложена 2670 конечными элементами и 3208 узлами, а для выработки квадратного поперечного сечения - 5357 конечными элементами 6373 узлами. В местах высоких градиентов напряжений сетка сгущена, причем степень дискретизации расчетной области повышалась постепенно до тех пор, пока изменения поля напряжений вблизи забоя стали несущественными. Размер расчетной области в поперечном направлении назначен равным шести радиусам выработки (6R), а в продольном - десяти (10R).

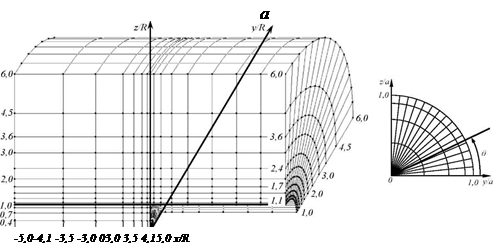
Рисунок 5 - Расчетные схемы к решению объемных задач для выработок круглой формы поперечного сечения

 

Для модели с квадратной формой поперечного сечения выработки линейные размеры устанавливались по отношению к условному радиусу R_y, связанному с площадью поперечного сечения выработки соотношением Ry = S/ π. Площадь поперечного сечения выработки различной формы была принята постоянной, а забой помещался в середине расчетного фрагмента, чтобы вызванные забоем возмущения в распределении напряжений затухали к торцам моделей.

Внешнее загружение модели производилось нормированными условными силами, определяемыми в соответствии с задаваемым соотношением λ между боковой P_y и вертикальной P_z нагрузками (0 ≤ λ ≤ 1). Компонента исходных напряжений по вертикальной оси принята равной единице, а по горизонтальной y - коэффициенту λ. При такой нагрузке в случае необходимости легко переходить от коэффициентов концентрации к реальным величинам напряжений путем умножения на вертикальную компоненту исходного поля Pz = γ H. Модуль упругости при определении деформаций также выражался в безразмерном виде E/P_z = 1000. Граничные условия на поверхностях симметрии и торцах фрагмента заданы таким образом, чтобы исключалось перемещение узлов перпендикулярно к ним, тогда продольные начальные напряжения Px на торцах модели связаны с основными влияющими факторами зависимостью:

Px = Pz (1+λ) ν (6)

 

где v- коэффициент Пуассона, v= 0,25.

Расчет производился с помощью программы «Лира-9», а результаты численного решения представлялись в виде табличных данных и графиков распределения напряжений в элементах и перемещений узлов в характерных продольных и поперечных сечениях, а также по контуру выработки на различном расстоянии от забоя.

Для суждения о внешнем виде функции влияния забоя следует проанализировать закономерности изменения вдоль выработки разности главных напряжений, определяющей в соответствии с теорией прочности Мора предельное состояние пород. Изменение разности коэффициентов концентрации главных напряжений Δ = k σ 1 – k σ 3 для круглого поперечного сечения выработки демонстрируется на рис. 6 в двух характерных точках контура, т.е. в боках (рис. 6, а) и кровле (рис. 6, б) выработки, а для квадратного в четырех характерных точках, а именно: в боках (рис. 7, а) и кровле (рис. 7, б) по осям симметрии, а также в боках (рис. 8, а) и кровле (рис. 8, б) вблизи угла выработки.

Вдоль выработки цилиндрической формы при приближении к забою со стороны нетронутого массива разность коэффициентов концентрации напряжений Δ в районе боков будущей выработки при всех значениях λ монотонно возрастает в результате передачи напряжений от вышележащей толщи через опережающий забой массив. В плоскости забоя градиент изменения напряжений достигает максимума, а вогнутость зависимости (рис. 6, а) плавно переходит в выпуклость, после чего изменение разности начинает убывать, а главные напряжения стремятся к своему пределу вне зоны влияния забоя. При этом доля прироста напряжений впереди забоя доходит до 40% от всего диапазона изменения параметра Δ, а разрушение в опережающем массиве может зарождаться в условиях обобщенного сжатия при значениях параметра Надаи-Лоде μσ = -(0,1...0,8).

В кровле круглой выработки (рис. 6, б) кривые изменения разности коэффициентов концентрации главных напряжений ведут себя по-разному в зависимости от λ. При напряженном состоянии, близком к гидростатическому, они подобны вышерассмотренным в боках выработки, а при малых значениях λ зависимости имеют совершенно иной вид. Первоначальный рост разности главных напряжений Δ в зоне опорного давления впереди забоя свидетельствует о передаче напряжений, вызванных образованием полости, перед забоем. Однако в пределах первой заходки разность главных напряжений резко снижается, главные площадки разворачиваются, так как напряжения теперь передаются через боковые стенки выработки, а в кровле (почве) выработки формируется зона разгрузки, где при λ < 0,33 на контуре δ₁ = 0, а δ ₂ и δ ₃ принимают значения меньше нуля, что соответствует условию обобщенного растяжения.

В общем, для выработки с квадратной формой поперечного сечения имеют место те же закономерности изменения вдоль выработки разности главных напряжений Δ, что и для выработки круглой формы. Локальные отличия объясняются особенностями породного контура, т. е. наличием углов и плоских участков. При подходе к забою разность Δ монотонно возрастает при всех значениях коэффициента бокового распора A как в боках (рис. 6, а) так и в кровле (рис. 6, б) выработки. Вблизи угла (5-й и 6-й элементы на рис. 5, б) в плоскости забоя вогнутость кривых плавно переходит в выпуклость (при 0 ≤ λ ≤ 0,3 с небольшим скачком), а далее вдоль выработки значения Δ, затухая, продолжают возрастать, стремясь к своему пределу вне зоны влияния забоя. При этом доля прироста напряжений впереди забоя составляет порядка 30%, причем весь диапазон изменения параметра при λ = 1 составляет 0 ≤ Δ ≤ 3,1, а при λ = λ = 0 – 1,0 ≤ Δ ≤ 2,6.

Рисунок 6 - Распределение разности коэффициента концентрации главных напряжений Δ для круглой выработки вдоль продольной оси в боках (а) и кровли (б) при различных значениях λ

 

В боках выработки (10-й элемент на рис. 5, б) плавный переход вогнутости кривой в выпуклость наблюдается при 0 ≤ λ ≤ 0,3. В остальных случаях, а в 1-м элементе кровли выработки при всех значениях Δ, в плоскости забоя отмечается резкий скачок разности главных напряжений, максимальная величина которого (Δ = 2,4) в 1-м и 10-м элементах соответствует гидростатическому напряженному состоянию (λ = 1).

В пределах первой заходки (x < 0,5a), после достижения максимума, величина разности коэффициентов концентрации главных напряжений Δ быстро снижается, например, в 1-м и 10-м элементах при λ = 1 до Δ = 0,8. Вследствие плоского контура выработки в кровле (почве) формируется зона разгрузки, где при x < 0,5 максимальное главное напряжение δ₁ ~ 0, а другие компоненты напряжений δ₂ и δ₃ имеют значения меньше нуля. При этом максимальное снижение разности главных напряжений в кровле выработки происходит при 0,4 ≤ λ ≤ 0,5. Далее с удалением от забоя разность коэффициентов концентрации главных напряжений Δ возрастает, причем в кровле (1-й элемент) лишь при λ > 0,8 её величина на контуре выработки превышает аналогичное значение в массиве до проведения выработки.

Таким образом, в плоскости забоя квадратной выработки разность главных напряжений (δ₁ - δ₃₎ в кровле (1-й элемент) и в боках (10-й элемент) превышает аналогичную величину, характерную для удаленных от забоя поперечных сечений выработки. Следовательно, в однородных и изотропных породах разрушение пород от сжатия в кровле и боках квадратной выработки вблизи её забоя является, зачастую, первичным, что способствует формированию более устойчивого к последующим изменениям формы контура состояния и уменьшает роль угла в формировании нового поля напряжений. В слоистых породных массивах, где прочность пород в связи с наличием поверхностей ослабления уменьшается, разрушение в кровле (почве) является ещё более вероятным. Поэтому ещё до попадания пород кровли (почвы) в зону разгрузки они могут быть ослаблены в опорной зоне впереди забоя, где наблюдается высокая концентрация главных напряжений и наибольшее значение их разности (δ₁ - δ₃₎.

Анализ распределения напряжений в окрестности забоя выработок различной формы поперечного сечения показал, что перераспределение исходного поля напряжений при сооружении выработки сплошным забоем в упругом породном массиве практически ограничивается областью, удаленной от забоя на расстояние 5R_y. При этом вдоль выработки в пределах зоны влияния забоя можно выделить три характерных участка: возрастания напряжений впереди забоя вследствие действия опорного давления с максимальной концентрацией в торцовом сечении выработки; скачкообразного изменения поля напряжений и разворота площадок главных напряжений в результате образования полости; постепенного роста напряжений (по модулю) на контуре выработки за её забоем до стабилизации поля в условиях плоской деформации.

Напряженное состояние породного массива вблизи забоя выработки с необходимой достоверностью определяется безразмерной функцией влияния забоя f (L/Rу), которая является множителем к компонентам начального поля напряжений при решении плоских задач и впереди забоя, независимо от формы выработки, изменяется по нелинейной зависимости от единицы (f = 1) до величины коэффициента опорного давления f = k, в плоскости забоя имеет скачек в результате образования полости, а позади забоя постепенно возрастает по экспоненциальной зависимости от f = 0,4-0,5 до единицы в условиях плоской деформации.

 

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: