Задание 2. Решение задачи компаундирования

Лабораторная работа №4

 

Цели работы: Решение задач линейного программирования в программной среде MathCad. Решение задач оперативного планирования химического производства Решение задачи компаундирования

 

Задание 1. Оперативное планирование аммиачно-азотного производства

Рассмотрим задачу оперативного планирования аммиачно-азотного производства. Необходимо рассчитать суточный выпуск продукции цехами аммиачно-азотного производства азотно-тукового комбината при условии достижения минимальных затрат на производство, соблюдении балансовой связи между цехами и ограничений, наложенных на объем производства некоторых цехов.

Производственная структура и связи между подразделениями представлены на рис. 1. Как видно из рисунка, аммиак является исходным продуктом для ряда цехов. Получающаяся при этом слабая азотная кислота, производство которой осуществляется в трех отдельных цехах по разным технологиям, в свою очередь, служит сырьем для дальнейшей переработки.

 

 

 

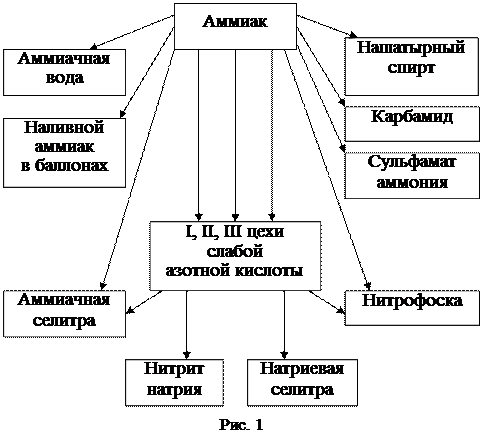
Материальные и энергетические потоки рассматриваемого производства характеризуются нормами расхода на 1 т полупродуктов и готовой продукции (для упрощения расчетов некоторые виды сырья не учитываются). Нормы представлены на рис. 2. Необходимо выполнять основные требования по выпуску продукции (см. рис. 3), и при этом не превышать запасы сырья и мощности производства (рис. 4 и 5).

 

	Цех
	аммиака	аммиачной воды	налива аммиака	нашатырного спирта	карбамида	сульфамата аммония	азотная кислота, цех I	азотная кислота, цех II	азотная кислота, цех III	аммиачной селитры	нитрофоски
аммиак		1,03	1,05	0,245	0,603	0,8	0,2946	0,292	0,29	0,212	0,086
природный газ
электроэнергии										15,7
пар					2,1	0,22				0,44	0,1
вода
апатит											0,234
азотная кислота										0,78
себестоимость 1 т		49,54	50,6	12,26	38,91	47,77	15,6	16,6	18,7	24,46	14,51

Рис. 2. Расходные коэффициенты сырья, полуфабрикатов и энергии
на 1 т производимой продукции

 

 

Продукция	Требование на суточный выпуск продукции
суммарный выпуск азотной кислоты по цехам
нашатырный спирт
карбамид
сульфамат аммония
аммиачная селитра

Рис. 3. Требования на суточный выпуск продукции

 

 

Цехи азотной кислоты	Прочие цехи
эл. энергия	аммиак	апатит	пар	эл. энергия	вода
	1109,2	257,4

Рис. 4. Расход на производство

 

 

	Цех	Мощность
	аммиака
	аммиачной воды
	налива аммиака
	нашатырного спирта
	карбамида
	сульфамата аммония
	азотная кислота, цех I
	азотная кислота, цех II
	азотная кислота, цех III
	аммиачной селитры
	нитрофоски

Рис. 5. Мощности цехов

Для решения задачи:

1. Создать новый документ MathCad.

2. Введем массив Рlimit, переменных, обозначающих предельные мощности цехов. Для этого ввести новую переменную Рlimit как одномерный массив (состоящий из 11 строк по числу цехов и 1 столбца) со значениями из таблицы рис. 5. Для создания массива использовать шаблон матрицы панели Vector and Matrix

3. Введем матрицу Norm расходных коэффициентов. Для этого ввести переменную Norm, которой присвоить в качестве значения матрицу из 8 строк и 11 столбцов. Значения элементов матрицы взять согласно рис. 2

 

4. Введем массив Р поисковых переменных, обозначающих расчетные мощности цехов. Для этого ввести новую переменную Р как одномерный массив (состоящий из 11 строк по числу цехов и 1 столбца) с нулевыми значениями

5. Сформируем целевую функцию. Целевой функцией являются затраты на производство.

Она имеет вид:

, (1)

где i – номер цеха, p _i – производительность i-го цеха (поисковые переменные), c _i – себестоимость продукции i-го цеха (последняя строка матрицы Norm).

Для формирования целевой функции создадим функцию пользователя с именем Zatr. Аргументами функции будут поисковые переменные Р

6. Теперь можно перейти к формированию задачи оптимизации. Поскольку в задаче есть ограничения, то необходимо сформировать блок ограничений.

В MathCad для открытия блока ограничений используется команда given.

Ввести слово given в документ ниже введенных ранее блоков.

7. Ниже слова given начнем формировать ограничения задачи.

8. Сначала сформируем требования по цехам азотной кислоты:

требование на суточный суммарный выпуск азотной кислоты по цехам (рис.3)

требование на расход электроэнергии по цехам азотной кислоты (рис. 4)

требование на расход аммиака по цехам азотной кислоты (рис. 4)

9. Далее сформируем

ограничение на расход воды по прочим цехам (рис. 4)

ограничение на расход аммиака по цехам азотной кислоты(рис. 4)

При вводе левой части ограничения используйте шаблон суммы панели Calculus.

ограничение на расход электроэнергии по прочим цехам (рис. 4)

ограничение на расход пара по прочим цехам (рис. 4)

ограничение на расход апатита по прочим цехам (рис. 4)

10. Затем сформируем ограничения на производительность цехов

аммиака (рис. 5)

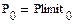
нитрофоски (рис. 5)

11. Также потребуем, чтобы производительность остальных цехов не превышала заданных пределов

 

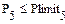
12. Далее, введем ограничения, соответствующие требованиям на суточный выпуск:

нашатырного спирта, карбамида, сульфамата аммония, аммиачной селитры (рис. 3)

 

 

 

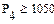
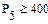
Теперь все ограничения сформированы. Все введенные ограничения линейны относительно поисковых переменных Р. Функция цели Zatr также линейна относительно Р.

Мы видим, что поставленная задача является задачей линейной оптимизации.

13. Завершим блок ограничений требованием на минимизацию затрат на производство, использую функцию MathCad minimize. В качестве аргументов функции используем матрицу поисковых переменных Р.

Для упрощения дальнейшей работы сохраним результаты функции minimize в переменной Р1

После ввода последнего блока MathCad приступит к решению задачи оптимизации.

В зависимости от сложности задачи решение занимает некоторый интервал времени. На этот период решаемый блок обведен зеленой рамкой.

По окончании решения зеленая рамка исчезает.

14. Используя контекстное меню функции minimize для выяснения, методы линейной или нелинейной оптимизации использовал MathCad. В случае неверной установки выберите вариант линейной оптимизации.

15. Теперь можно вывести результаты. Для этого переведите курсор ниже и введите блок вычисления значения целевой функции при найденных значениях поисковых переменных, которые мы сохранили в переменной Р1

Используя команду форматирования результата, выведите результат в виде, приведенном выше.

16. Выведем также и найденные значения поисковых переменных, сохраненные в переменной Р1:

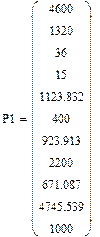
Используя команду форматирования результата, приведите вид матрицы Р1 к показанному выше виду.

17. Сохраните документ под именем Азотно-туковый завод.

 

Задание 2. Решение задачи компаундирования

Рассмотрим задачу получения бензина заданного октанового числа. Будем предполагать, что зависимость октанового числа получаемой смеси зависит от октановых числе компонентов смеси линейно.

Нужно получить 5 т бензина с октановым числом 76, используя выпускаемые компоненты с октановыми числами 83, 72, 66. Известно, что стоимости компонентов соотносятся как 2:1,5:1.

1. Открыть новый документ MathCad.

2. Обозначив количества компонентов через запишем вид целевой функции, соответствующей затратам на закупку компонентов смеси.

3. При формировании смеси будем предполагать, что будем получать смесь с октановым числом, большим, чем требуемое на некую величину 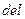. Задать значение величине, равное 0.2

4. В нашей задаче присутствуют ограничения, поэтому ниже следует ввести слово given.

5. Сформируем ниже ограничения задачи. Первое ограничение соответствует получению 5 тонн бензина

6. Второе ограничение соответствует требованию на значение октанового числа получаемой смеси. Опираясь на предположение о линейной зависимости, запишем ограничение

7. Введем ограничения на возможные значения количеств компонентов –они должны быть положительны. Для этого ввести ограничение

 

 

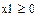
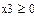
8. В строке ниже завершить блок вызовом функции minimize, сохранив результаты в переменных

9. Проверим, каковы затраты на получение смеси. Ввести ниже блок

10. Сохранить документ под именем Компаундирование

11. Провести вычисления для .

Поделиться:

Воспользуйтесь поиском по сайту: