 |
Оформите электронную таблицу согласно приведенному рисунку.
|
|
|
|
Лабораторная работа 9
Оптимизация ректификационной колонны разделения пропан-пропиленовой фракции
Провести моделирование разделения близкокипящей смеси в ректификационной колонне. В качестве разделяемой смеси взять пропан-пропиленовую фракцию с параметрами:
Температура 40 °С; Давление 17 бар;
Расходы компонентов:
Этан 10 кг/час;
Пропилен 10500 кг/час;
Пропан 4400 кг/час;
н-Бутан 90 кг/час.
Обеспечить качество разделения с долей пропилена по верху колонны не менее 95% массовых, долей пропана по кубу колонны не менее 95% массовых.
Выполнение задания:
1. Собрать собственный набор компонентов Set-1, включающих указанные вещества.
2. Настроить пакет расчета свойств веществ, задав модель расчета парожидкостного равновесия Peng-Robinson (Пенг-Робинсон).
3. Перейдите в расчетную среду из окна Диспетчера базиса.
4. Сохраните задание под именем PPFCOLUMN_Имя, где Имя – Ваша фамилия.
5. Используя Рабочую тетрадь сформируйте поток питания с именем Feed1. Укажите температуру, давление сырьевого потока. Общий расход потока не задавайте.
6. На вкладке Composition (Состав) задайте массовые расходы для каждого из компонентов.
7. Для моделирования процесса разделения будем использовать модуль ректификационной колонны.
Выбрать соответствующую модель в Кассе объектов и щелкните в окне программы, где хотите расположить пиктограмму.
8. В окне Инспектора ввода колонны укажите следующие сведения о колонне:
| Конденсатор | Полный (Total) |
| Давление в кондесаторе | 15.5 бар |
| Перепад давления в конденсаторе | 0 бар |
| Давление в ребойлере | 17 бар |
| Перепад давления в ребойлере | 0 бар |
| Количество тарелок | |
| Поток питания | Feed1 |
| Тарелка питания | |
| Поток дистиллята | Propen |
| Кубовый продукт | Propan |
| Поток энергии для коненсатора | Heat Cond |
| Поток энергии для ребойлера | Heat Rebr |
9. Задайте спецификации колонны. В качестве спецификаций колонны следует выбрать:
|
|
|
а) Флегмовое число, задав его значение равным 10

б) Массовый расход кубового продукта, задав его значение равным 4000 кг/ч

Остальные спецификации удалите.
10. Рассчитайте колонну.
Оптимизация стационарного режима работы колонны
Проведем оптимизацию режима работы пропан-пропиленовой колонны, максимизируя прибыль при получении продукта требуемого качества.
В качестве критерия оптимальности будем использовать функцию Прибыли F, которую запишем как:
F = a*D – b*R, (4)
где D – массовый расход дистиллята, кг/ч, R – флегмовое число, a, b – ценовые коэффициенты,  ,
,  .
.
На получаемые продукты наложим ограничения
 , (5)
, (5)
 , (6)
, (6)
где  ,
,  – содержание пропилена в дистилляте и пропана в кубовом продукте соответственно.
– содержание пропилена в дистилляте и пропана в кубовом продукте соответственно.
В качестве поисковых переменных выберем
R – флегмовое число
W – массовый расход кубового продукта, кг/ч.
На поисковые переменные наложим ограничения
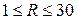 , (7)
, (7)
 . (8)
. (8)
Выполнение задания:
11. Вызвать окно Оптимизатора.
12. На вкладке Variables добавить 2 поисковые переменные:
Флегмовое число (Reflux ratio) и Расход кубового продукта (Liquid Flow) колонны.


Задание целевой функции и ограничений задачи.
Целевая функция опирается на значения флегмового числа, массового расхода кубового продукта, а также на значения ценовых коэффициентов.
Ограничения вычисляются на основе значений Массовой доли пропилена в дистилляте (поток Propen) и Массовой доли пропана в кубовом продукте (поток Propan).
Для формирования целевой функции и ограничений необходимо сформировать Электронную таблицу Оптимизатора.
Оформите электронную таблицу согласно приведенному рисунку.
а) Введите текст, как показано на рисунке.
|
|
|
б) Введите константы, на которые опирается вычисление Прибыли.
Для этого занести в ячейку В1 значение 1,
в ячейку В6 число 10,
в ячейки С1, С2 ввести числа 0,95.

г) Импортировать переменные в ячейки таблицы:
в ячейку В1 – массовый расход дистиллята – Массовый расход потока Propen;
в ячейку В5 – значение Флегмового числа колонны,
в ячейку С5 импортировать из потока Propen Массовую долю вещества Propen (Master Comp Mass Frac)

аналогично в ячейку С6 импортировать из потока Propan массовую долю вещества Propan (Master Comp Mass Frac)
д) ввести в ячейки В3, В7, D7 формулы, на основе которых будет получено значение прибыли


15. Перейдите в окно Оптимизатора и на вкладке Functions укажите
а) адрес ячейки, в которой находится вычисленное значение целевой функции – ячейка D7;
б) укажите, что нужно максимизировать целевую функцию.

16. Сформируйте ограничения задачи, как показано на рисунке.
Добавление нового ограничений проводится кнопкой Add (Добавить).
В строке ограничения в столбце LHS Cell указывается адрес ячейки, в которой находится вычисленное значение ограничения.
В нашем случае это ячейки С5 и С6.
В строке ограничения в столбце RHS Cell указывается адрес ячейки, в которой находится граничное значение для ограничения.
У нас используются требования, записанные в ячейках С2, С3.
В столбце Cond выбирается знак сравнения.
В столбце Penalty Value указывается значение штрафного коэффициента, на которое нужно домножать отклонение ограничения от границы.
Поскольку в нашем случае значения ограничений малы по сравнению со значением целевой функции, мы будем использовать большие величины штрафных коэффициентов 100000000

17. Настройте метод решения задачи оптимизации, для чего перейдите на вкладку Parameters (Параметры).
Будем использовать метод Последовательного квадратичного программирования SQP.
Настройте остальные параметры метода, как предложено на рисунке.

18. Перейдите на вкладку Monitor и запустите решение задачи Start.
В случае, если метод не достигнет решения, запустите его еще раз, пока не будет получено сообщение о выполнении задачи.

19. Сохраните задание. Предъявите преподавателю.
|
|
|


