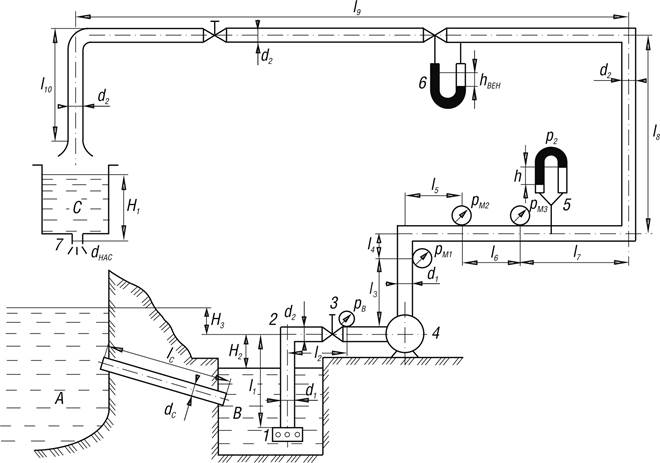
Схема циркуляционной установки

 

 

Расчетная часть

Исходные данные

Величина	Вариант
	19
H3, м	2,5
l 1, м	12
l 2, м	8
l 3, м	7
l 4, м	6
l 5, м	7
l 6, м	150
l 7, м	50
l 8, м	6
l 9, м	280
l 10, м	15
l с, м	55
l экв, м	4
d 1, мм	159
d 2, мм	125
d вен, мм	60
d нас, мм	65
∆ мм	0,4
∆ с мм	0,4
ζ кор	10
ζ кол	0,8
ζ зад	2,0
ρ 1кг/м3	870
ν 1см2/с	0,12
ρ 2кг/м3	730
μ нас	0,82
μ вен	0,95
P в, кПа	47
P м1, кПа	340
h вен, мм.рт.ст	286

 

Определяемые параметры

1) Определить геометрическую высоту всасывания насоса Н₂.

2) Определить показание дифманометра (или дифпьезометра) скоростной трубки.

3) Построить эпюру скоростей для сечения в месте установки скоростной трубки.

4) Определить показание дифманометра расходомера Вентури (h _вен).

5) Определить установившейся уровень жидкости в промежуточной емкости Н1.

6) Определить разность показаний манометров Р_м2 и Р_м3.

7) Определить суммарные потери напора в местных сопротивлениях нагнетательной линии и их суммарную эквивалентную длину.

8) Определить необходимый диаметр самотечного трубопровода d_c, обеспечивающий установление заданного постоянного уровня в верхнем резервуаре Н₃.

9) Определить минимальную толщину стальных стенок трубы d ₂, при которой не происходит её разрыва в момент возникновения прямого гидравлического удара.

10) Определить полезную мощность насоса.

 

 

4.1. Определение геометрической высоты всасывания насоса Н₂.

 

4.1.1. Для определения геометрической высоты всасывания насоса Н₂ рассмотрим два сечения А-А (поверхность жидкости в нижнем резервуаре В) и В-В (в месте установки вакуумметра Р_в во всасывающей линии насосной установки). Мы имеем дело с установившимся движением вязкой несжимаемой жидкостью. Запишем уравнение Бернулли для сечения А-А и В-В:

         …(1)        

где , - расстояния от сечений А-А и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости (м);

, - давления в сечениях А-А и В-В соответственно (Па);

- плотность циркулирующей жидкости (кг/м³);

g - ускорение свободного падения (м²/с);

V_{A - A}, V_{B - B} - скорость течения жидкости в сечение А-А и В-В соответственно (м/с);

, - коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях А-А и В-В соответственно;

- потери напора на участках между выбранными сечениями.

Выберем сечение А-А за начало отсчёта, тогда z_А-А=0 и z_В-В=Н₂.

V_{A - A} =0, так как уровень в нижнем резервуаре В установившийся.

, так как резервуар В открыт.

- разность атмосферного и вакуумного давления.

Для решения практических задач коэффициент Кориолиса можно принять равным единице, т.е. .

 , где Q – расход жидкости (м³/с); S - площадь поперечного сечения (м²).

В результате формула (1) примет вид:

  …(2)

Для определения Н₂ необходимо определить расход Q и потери напора h_A-B.

4.1.2. Для определения расхода жидкости рассмотрим ртутный дифманометр расходомера Вентури. 

Запишем уравнение неразрывности для сечений 1-1 и 2-2:

(1)

Выразим из (1) скорость :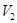

(2).

Запишем уравнение Бернулли Для двух сечений 1-1 и 2-2:

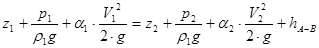(3)

где , - расстояния от сечений А-А и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости (м);

, - давления в сечениях А-А и В-В соответственно (Па);

- плотность циркулирующей жидкости (кг/м³);

g - ускорение свободного падения (м²/с);

V ₁ , V ₂ - скорость течения жидкости в сеченьях А-А и В-В соответственно (м/с);

, - коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях А-А и В-В соответственно;

- потери напора на участках между выбранными сечениями.

Выберем ось трубопровода за начало отсчёта, тогда z₁=z₂=0, т.к. трубопровод горизонтален. Предположим, что по трубопроводу течёт идеальная жидкость, что позволяет не учитывать потери напора h_A-B=0.

α₁₌α₂=1, (для практических расчётов).

Запишем (3) с учётом всех утверждений:

(4).

 

Выразим из (4) с учётом (2):

(5)

Из рисунка видно, что , где    (6)

Теоретический расход будет меньше, т.к. существуют потери напора, учтём это с помощью поправочного коэффициента, который называется коэффициентом расхода μ.

, где S₁= S _вен (7).

Подставим в (7) уравнение (5) (с учётом (6)):

, где

В итоге имеем:

4.1.3. Определим потери напора h_А-В.

 

h _А-В = h _д +h_м (3), где h _д - потери напора по длине трубопровода (м); h_м - потери напора от местных сопротивлений.

h _м = h _кор +h_кол+h_зад, где h _кор - потери напора на коробке всасывающей линии (м);

h _кол - потери напора на колене всасывающей линии (м);

h _зад - потери напора на задвижке всасывающей линии (м).

  

h _д = h _д1 +h_д2, где h _д1 - потери напора на участке трубопровода l₁;

h _д2 - потери напора на участке трубопровода l₂.

 ; ;

 где - коэффициент гидравлического сопротивления для соответствующего участка.

Для определения λ₁ и λ₂ необходимо определить режим течения жидкости на соответствующих участках трубопровода. Для этого определим числа Re для этих участков:

где ν - кинематическая вязкость циркуляционной жидкости (м²/с).

Имеем, что Re₁>Re_кр=2300  на участке трубопровода l ₁ турбулентный режим течения;

Re₂>Re_кр=2300  на участке трубопровода l ₂ турбулентный режим течения.

Определим тип трубопровода (шероховатый или гладкий) на участках трубопровода l₁ и l₂.

Для этого определим значения величин обратной относительной шероховатости для обоих рассматриваемых участков:

Оба участка принадлежат зоне шероховатых труб, т.к. их числа Re принадлежат промежуткам:  

 для первого и второго промежутков соответственно. Следовательно, для определения λ₁ и λ₂ воспользуемся формулой Альтшуля:

Найдём суммарные потери напора для участков l ₁ и l ₂:

Подставим полученные нами значения в формулу (3) и получим необходимую величину:

h _А-В = h _д +h_м=0,61+1,02=1,63м.

 

По формуле (2) определим геометрическую высоту всасывания насоса Н₂:

 

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: