 |
Задание на курсовую работу
|
|
|
|
Содержание
Введение
1. Задание на курсовую работу
2. Разработка алгоритма решения задачи
3. Разработка программы
4. Тестирование и отладка программы
5. Документирование программы
Заключение
Литература
Приложение
Введение
Целью данной курсовой работы является получение навыков разработки, отладки, тестирования и документирования программ на языке высокого уровня при решении на ЭВМ прикладной инженерной задачи.
В ходе выполнения курсовой работы решены следующие задачи:
Разработан алгоритм синтеза пленочного резистора по заданным параметрам исходного резистора.
Разработана программа реализации данного алгоритма на языке С++.
Выполнена отладка и тестирование программы.
Составлена документация на программу и инструкция пользователя программой.
Программа оттранслирована и скомпонована в среде MVS-6 в виде консольного приложения.
Программа предназначена для работы под управлением операционной системы WINDOWS XP или ее более ранних версий.
При работе программы используется стандартное оборудование компьютера: процессор типа PENTIUM, жесткий диск, монитор, клавиатура и мышь.
Задание на курсовую работу
Прикладной инженерной задачей в данной курсовой работе является синтез интегральных резисторов микросхем. Резисторы микросхемы представляют собой полоски тонкой пленки в форме прямоугольника или меандра, как показано на рис. 1.
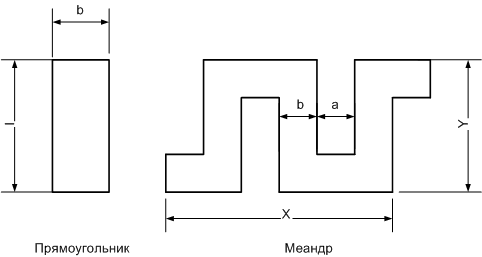
Рис. 1 Форма пленочного резистора
Расчет резистора заключается в определении его размеров – длины  и
и  ширины в случае прямоугольных пленок и ширины
ширины в случае прямоугольных пленок и ширины  , расстояния
, расстояния 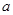 между полосками, размеров
между полосками, размеров  и
и  , а также числа звеньев
, а также числа звеньев  в случае пленок в форме меандра.
в случае пленок в форме меандра.
|
|
|
Исходные данные представлены в виде двух групп – данные с переменными и постоянными значениями.
Таблица 1. Исходные данные с переменными значениями
| Обозначения и ед |  , кОм , кОм
|  , кОм/кв , кОм/кв
| 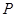 , мВт , мВт
|  , мВт/мм2 , мВт/мм2
|
| Наименование | Номинальное сопротивление | Сопротивление квадрата резистивной пленки | Мощность рассеяния резистора | Максимальная удельная мощность рассеяния резистивной пленки |
| Диапазон значение | 0.05..10000 | 0.01..50 | 5..50 | 10..30 |
Таблица 2. Исходные данные с постоянными значениями
| Обозначения и единицы |  , мм , мм
| 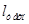 , мм , мм
|  , мм , мм
|  , мм , мм
| 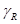
|  , мм , мм
|  , мм , мм
|
| Наименование | Минимально допустимая ширина и длина резистора | Погрешность воспроизведения ширины и длины резистора | Допустимая погрешность коэффициента формы | Минимальное расстояние между полосками резистора сложной формы | Шаг координатной сетки | ||
| Диапазон значение | 0.1 | 0.3 | 0.01 | 0.03 | 0.1 | 0.3 | 0.01 |
Расчет резисторов выполняется в следующей последовательности.
Определяется значение коэффициента формы
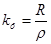 (1)
(1)
Выбирается форма резистора
1. При  – резистор прямоугольной формы,
– резистор прямоугольной формы,
2. При  – резистор прямоугольной формы, у которого
– резистор прямоугольной формы, у которого  ,
,
3. При  – резистор сложной формы типа меандр,
– резистор сложной формы типа меандр,
4. При  – резистор не может быть сконструирован.
– резистор не может быть сконструирован.
Связь между размерами резистора прямоугольной формы определяется соотношением
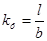 (2)
(2)
В случае 1
 , (3)
, (3)
где
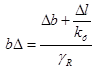 , (4)
, (4)
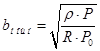 . (5)
. (5)
После определения  длина вычисляется по формуле (2). Полученные значения ширины и длины округляются с учетом шага координатной сетки по формуле
длина вычисляется по формуле (2). Полученные значения ширины и длины округляются с учетом шага координатной сетки по формуле
 , (6)
, (6)
где  ,
,  – целая часть числа.
– целая часть числа.
В случае 2
Определяется длина из выражения
 , (7)
, (7)
где
 , (8)
, (8)
 . (9)
. (9)
Ширина  определяется по формуле (2) и значения ширины и длины округляются по формуле (6).
определяется по формуле (2) и значения ширины и длины округляются по формуле (6).
|
|
|
В случае 3
Определяется ширина резистора по формулам (3)–(5). Определяется длина средней линии меандра из выражения
 . (10)
. (10)
Задается расстояние  . Если
. Если 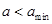 , то
, то  .
.
Определяется шаг одного звена меандра
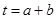 . (11)
. (11)
Определяется по приближенной формуле число звеньев меандра
 . (12)
. (12)
Вычисляется длина и ширина меандра
 , (13)
, (13)
 (14)
(14)
Проверяется условие
 . (15)
. (15)
Если это условие выполняется, то расчет завершается. Иначе, увеличивается расстояние  на величину
на величину  и повторяются вычисления по формулам (11)–(14). Если при 10-ти кратном повторении соотношение (15) не выполняется, то расчет завершается с фиксированием факта невозможности синтеза резистора.
и повторяются вычисления по формулам (11)–(14). Если при 10-ти кратном повторении соотношение (15) не выполняется, то расчет завершается с фиксированием факта невозможности синтеза резистора.
Рассмотренная методика расчета применяется к заданному количеству резисторов 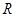 . Диапазон значений
. Диапазон значений 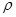 и значение
и значение  для всех резисторов принимается одинаковыми.
для всех резисторов принимается одинаковыми.
|
|
|


