Свойства дисперсии случайной величины.

Свойства математического ожидания.

1. Математическое ожидание постоянной величины равно самой постоянной: .

2. Постоянный множитель можно выносить за знак математического ожидания .

3. Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий .

4. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий .

5. Если все значения случайной величины увеличить на постоянную С, то на эту же постоянную увеличится математическое ожидание этой случайной величины. .

6. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю .

Найдем математическое ожидание в примере 1

Пример 2.Известны законы распределения случайных величин X и Y – числа очков, выбиваемых первым и вторым стрелками.

xi
pi	0,15	0,11	0,04	0,05	0,04	0,10	0,10	0,04	0,05	0,12	0,20

yi
pi	0,01	0,03	0,05	0,09	0,11	0,24	0,21	0,10	0,10	0,04	0,02

Необходимо выяснить, какой из двух стрелков стреляет лучше.

Очевидно, что из двух стрелков лучше стреляет тот, кто в среднем выбивает большее количество очков

17.3. Дисперсия дискретной случайной величины.

Дисперсией случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:

.

Если случайная величина Х – дискретная с конечным числом значений, то , где

Если случайная величина Х – дискретная с бесконечным счетным множеством значений, то .

Средним квадратичным отклонением (стандартным отклонением или стандартом) называется .

Свойства дисперсии случайной величины.

1. Дисперсия постоянной величины равна нулю: .

2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат .

3. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:

4. Дисперсия алгебраической суммы конечного числа случайных величин равна сумме их дисперсий .

Пример 1.

Пример 2. Известны законы распределения случайных величин X и Y – числа очков, выбиваемых первым и вторым стрелками.

xi
pi	0,15	0,11	0,04	0,05	0,04	0,10	0,10	0,04	0,05	0,12	0,20

 

yi
pi	0,01	0,03	0,05	0,09	0,11	0,24	0,21	0,10	0,10	0,04	0,02

Необходимо выяснить, какой из двух стрелков стреляет лучше.

Вычислить дисперсию и среднее квадратическое отклонение.

17.5. Непрерывные случайные величины.

Случайная величина Х называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.

Функция распределения непрерывной случайной величины.

Функцией распределения случайной величины X называется функция , выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х.

.

Свойства функции распределения:

1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей .

2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси, т.е. если , то .

3. , .

4. Вероятность попадания случайной величины Х в интервал равна приращению ее функции распределения на этом интервале: .

Плотность вероятности.

Плотностью вероятности непрерывной случайной величины Х называется производная ее функции распределения.

.

График плотности вероятности называется кривой распределения.

Свойства плотности вероятности:

1. Плотность вероятности – неотрицательная функция .

2. Вероятность попадания непрерывной случайной величины в интервал равна определенному интегралу от ее плотности вероятности в пределах от а до b .

3. Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле

4. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице: .

Геометрически свойства плотности вероятности означают, что ее график лежит не ниже оси абсцисс, и полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.

Для непрерывной случайной величины Х:

, если интеграл абсолютно сходятся;

или , если приведенные интегралы сходятся.

Пример 3. Функция распределения случайной величины Х определяется выражением

Найти: а) плотность распределения вероятностей, б) вероятность попадания величины Х на участок от 0,25 до 0,5.

а)

б)

Пример 4. Непрерывная случайная величина Х подчинена закону распределения с плотностью

Найти: а) функцию распределения , б) вероятность попадания случайной величины Х на участок от 0 до

Если , то

Если , то

Если , то

17.6. Мода и медиана. Квантили. Моменты случайных величин.

Модой случайной величины Х называется ее наиболее вероятное значение (для которого вероятность или плотность вероятности достигает максимума).

Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.

Медианой непрерывной случайной величины Х называется такое ее значение, для которого , т.е. вероятность того, что случайная величина примет значение, меньшее медианы или большее ее, одна и та же и равна .

Геометрически вертикальная прямая, проходящая через точку с абсциссой, равной , делит площадь фигуры под кривой распределения на две равные части.

Квантилем уровня q называется такое значение случайной величины, при котором функция ее распределения принимает значение, равное q, т.е. .

Медиана случайной величины есть квантиль уровня 0,5. Квантили и называются верхним и нижним квантилем. Квантиль называется процентной точкой. .

18. Основные законы распределения.

18.1. Биноминальный закон распределения.

Дискретная случайная величина Х имеет биноминальный закон распределения, если она принимает значения 0, 1, 2, …, m, …, n с вероятностями , где , , .

Биноминальный закон распределения представляет собой закон распределения числа наступлений события А в п независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р.

Математическое ожидание случайной величины Х, распределенной по биноминальному закону, , а ее дисперсия .

Биноминальный закон распределения используется в теории и практике статистического контроля качества продукции, при описании функционирования систем массового обслуживания, в теории стрельбы и др.

Пример. В семье 5 детей. Вероятность рождения мальчика равна 0,515. Составить закон распределения числа мальчиков в семье. Найти математическое ожидание и дисперсию этой величины.

, , ,

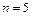xi
pi	0,0268	0,1425	0,3026	0,3213	0,1706	0,0362

 

18.2. Закон распределения Пуассона.

Дискретная случайная величина Х имеет закон распределения Пуассона, если она принимает значения 0, 1, …, т, … (бесконечное, но счетное множество значений) с вероятностями , где .

Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру этого закона, т.е. , .

При, , , 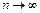закон распределения Пуассона является предельным случаем биноминального закона. Так как при этом вероятность наступления события в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.

18.3. Геометрическое распределение.

Дискретная случайная величина Х = т имеет геометрическое распределение, если она принимает значения 1, 2, …, т, … (бесконечное, но счетное множество значений) с вероятностями , где , , .

Математическое ожидание случайной величины, имеющей геометрическое распределение с параметром р равно , а ее дисперсия .

18.4. Гипергеометрическое распределение.

Дискретная случайная величина Х имеет гипергеометрическое распределение, если она принимает значения 1, 2, 3, …, min (n, M) с вероятностями , где , , ; N, M, n – натуральные числа.

Гипергеометрическое распределение имеет случайная величина – число объектов, обладающих заданным свойством, среди п объектов, случайно извлеченных (без возврата) из совокупности N объектов, M из которых обладают следующим свойством.

Гипергеометрическое распределение можно рассматривать как модификацию биноминального распределения для случая конечной совокупности, состоящей из N объектов, М из которых обладают этим свойством.

При функция вероятностей гипергеометрического распределения стремится к соответствующей функции биноминального распределения.

18.5. Равномерный закон распределения.

Непрерывная случайная величина имеет равномерный закон распределения на отрезке , если ее плотность вероятности постоянна на этом отрезке и равна нулю вне его, т.е.

.

Функция распределения случайной величины Х, распределенной по равномерному закону, есть

математическое ожидание , а дисперсия

18.6. Показательный (экспоненциальный) закон распределения.

Непрерывная случайная величина Х имеет показательный (экспоненциальный) закон распределения с параметром , если ее плотность вероятности имеет вид:

Функция распределения случайной величины Х, распределенной по показательному (экспоненциальному) закону, есть

математическое ожидание , .

Показательный закон распределения играет большую роль в теории массового обслуживания и теории надежности.

18.7. Нормальный закон распределения.

Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами а и 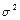, если ее плотность вероятности имеет вид .

Нормальный закон распределения является предельным законом, к которому приближаются другие законы распределения при некоторых типичных условиях. Этот закон наиболее часто встречается на практике. Кривая нормального распределения называется нормальной или гауссовой кривой.

Математическое ожидание случайной величины Х, распределенной по нормальному закону, равно параметру а этого закона, т.е. , а ее дисперсия – параметру , т.е. .

Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(Х) по формуле .

Случайная величина, распределенная по нормальному закону, обладает следующими свойствами:

1. Вероятность попадания случайной величины Х в интервал равна , где , .

2. Вероятность того, что отклонение случайной величины Х от математического ожидания не превысит величину (по абсолютной величине), равна , где .

Правило трех сигм.

Если случайная величина Х имеет нормальный закон распределения с параметрами а и , то практически достоверно, что ее значения заключены в интервале .

Пример. Полагая, что рост мужчины определенной возрастной группы есть нормально распределенная случайная величина Х с параметрами , найти:

1. а) выражение плотности вероятности и функции распределения случайной величины Х; б) доли костюмов 4-го роста (176 – 182 см) и 3-го роста (170 – 176 см), которые нужно предусмотреть в общем объеме производства для данной возрастной группы; в) квантиль и 10% точку случайной величины Х.

2. Сформулировать «правило трех сигм» для случайной величины Х.

1. а)

б) Доля костюмов 4-го роста (176 – 182 см) в общем объеме производства определяется по формуле как вероятность

Долю костюмов 3-го роста (170 – 176 см) можно высчитать проще, учитывая, что данный интервал симметричен относительно математического ожидания

в) Квантиль случайной величины Х найдем из уравнения с учетом

Это означает, что 70% мужчин данной возрастной группы имеют рост до 176 см. 10% точка – это квантиль , т.е. 10% мужчин имеют рост не менее 181 см.

2. Практически достоверно, что рост мужчин данной возрастной группы заключен в границах

19. Закон больших чисел.

Под законом больших чисел в широком смысле понимается общий принцип, согласно которому совокупное действие большого числа случайных факторов приводит (при некоторых весьма общих условиях) к результату, почти независящему от случая. Т.е. при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью определенности. (А.Н. Колмогоров)

19.1. Неравенство Маркова (лемма Чебышева).

Если случайная величина Х принимает только неотрицательные значения и имеет математическое ожидание, то для любого положительного числа А верно неравенство .

19.2. Неравенство Чебышева.

Для любой случайной величины, имеющей математическое ожидание и дисперсию, справедливо неравенство

. .

Первое неравенство устанавливает верхнюю границу вероятности рассматриваемого события, а вторая – нижнюю границу.

19.3. Теорема Чебышева.

Если дисперсии п независимых случайных величин ограничены одной и той же постоянной, то при неограниченном увеличении числа п средняя арифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий , т.е.

.

Если независимые случайные величины имеют одинаковые математические ожидания, равные а, а их дисперсии ограничены одной и той же постоянной, то неравенство Чебышева примет вид

.

 

Поделиться:

Воспользуйтесь поиском по сайту: