Лабораторная работа №2.

ПОСТРОЕНИЕ МОДЕЛИ НЕЛИНЕЙНОЙ ПАРНОЙ РЕГРЕССИИ

Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.

Примеры регрессий, нелинейных по объясняющим переменным, но линейных по оцениваемым параметрам:

- полиномы разных степеней

- равносторонняя гипербола .

Примеры регрессий, нелинейных по оцениваемым параметрам:

- степенная ;

- показательная ;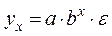

- экспоненциальная .

Наиболее часто применяются следующие нелинейные модели регрессий:

гиперболы – ;

параболы – ;

показательной функции ;

степенной функции – и др.

Лабораторная работа №1.

Вычисление коэффициентов уравнения нелинейной регрессии

Построению нелинейных регрессионных моделей предшествует процедура линеаризации переменных.

Линеаризация – (от лат. linearis — линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной. Методы линеаризации имеют ограниченный характер, т. е. эквивалентность исходной нелинейной системы и её линейного приближения сохраняется лишь для ограниченных пространственных или временных масштабов системы, либо для определенных процессов, причем, если система переходит с одного режима работы на другой, то следует изменить и её линеаризированную модель. Применяя линеаризацию, можно выяснить многие качественные и особенно количественные свойства нелинейной системы.

Для нелинейных уравнений регрессии, приводимых к линейным с помощью преобразования (x, y) → (x’, y’), система нормальных уравнений имеет вид:

в преобразованных переменных x’, y’.

Коэффициент b при факторной переменной x имеет следующую интерпретацию: он показывает, на сколько изменится в среднем величина y при изменении фактора x на 1 единицу измерения.

Гиперболическая регрессия: .

Линеаризующее преобразование: .

Тогда

.

Экспоненциальная регрессия: .

Линеаризующее преобразование: .

Степенная функция: .

Линеаризующее преобразование: .

.

Переход к параметру a уравнения степенной зависимости производят c помощью потенцирования по формуле:

.

Показательная функция: .

Линеаризующее преобразование: .

Переход к параметрам уравнения показательной зависимости (a, b) производят по формулам:

; .

Логарифмическая функция: .

Линеаризующее преобразование: .

Задача

Для определения зависимости между рождаемостью в России (переменная y измеряемая в тыс. чел.) и средней заработной платой (переменная x, измеряемая в руб.) были проведены исследования, результаты которых представлены в таблице 1.

Таблица 1.

Годы	Рождаемость в тыс. чел. y	Средняя заработная плата, руб. в мес. x
	886,9	2290,1
	928,6	3078,4
	998,1	3947,2
	1050,6	5170,4
	1074,3	6410,4
	1036,9	8023,2

Для характеристики зависимости у от х рассчитать параметры следующих функций:

- равносторонней гиперболы;

- степенной функции;

- показательной функции.

Решение.

1. Уравнение равносторонней гиперболы линеаризуется , тогда .

2. Для расчета используем данные таблицы 2.

Годы
	886,9
	928,6
	998,1
	1050,6
	1074,3
	1036,9
Итого
Среднее значение

 

Значения параметров регрессии а и b рассчитываем по формулам:

; .

3. Запишите полученное уравнение регрессии.

4. С помощь линеаризующих преобразований постройте уравнение регрессии для степенной и показательной функций.

Лабораторная работа №2.

Вычисление индекса корреляции и средней ошибки аппроксимации

Тесноту связи изучаемых явлений в нелинейных регрессиях оценивает индекс корреляции, который вычисляется по формуле:

; .

Средняя ошибка аппроксимации ‑ среднее отклонение расчетных значений от фактических:

.

Допустимый предел значений ‑ не более 8 ‑ 10%.

Задача

1. Рассчитать индекс корреляции и среднюю ошибку аппроксимации для нелинейных регрессий Лабораторной №1.

2. Определить по какому уравнению регрессии получена наибольшая оценка тесноты связи.

3. Сделать выводы.

Поделиться:

Воспользуйтесь поиском по сайту: