Определение критической глубины.

Введение

Курсовая работа рассматривает расчет целого комплекса взаимосвязанных сооружений: канала (при равномерном движении потока), быстротока, гасителя энергии, многоступенчатого перепада. При расчете перечисленных сооружений необходимо решить много побочных вопросов, а именно: исследование дифференциального уравнения неравномерного движения жидкости, построения кривой свободной поверхности, необходимость гасителя энергии и т.д.

Из вышеизложенного следует, что выполнение данной курсовой работы требует знания практически всего курса гидравлики и закрепляет эти знания.

Основными нормативными документами при проектировании водоотводных сооружений являются:

1) строительные нормы и правила. Автомобильные дороги (СНиП 2.05.02-85);

2) строительные нормы и правила. Мосты и трубы (СНиП 2.01.14-83);

3) строительные нормы и правила. Определение гидрологических характеристик (СНиП 2.01.14-83);

4) инструкция по расчету стоков с малых бассейнов (ВСН 63-76).

 

 

 

1. ИСХОДНЫЕ ДАННЫЕ

 

Исходные данные для курсовой работы приведены в таблице 1.1.

Таблица 1.1. Исходные данные.

№ варианта	Обозначение величин
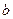
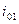
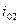
	6,3	1,5	0,001	0,17	0.0025		3,0	1,5	0,0250

 

– расход, ;

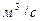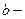ширина канала понизу, ;

уклон подводящего канала;

уклон быстротока;

уклон отводящего канала;

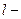длина быстротока, ;

высота перепада, ;

коэффициент заложения откоса канала;

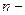коэффициент шероховатости стенок канала.

 

 

2. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ВОДОПРОПУСКНЫХ СООРУЖЕНИЙ

Подводящий канал

Устройство подводящего канала необходимо для принятия вод, стекающих по склонам к логу, и подведения к трубе, мосту или быстротоку. Искусственные подходные русла должны обеспечивать пропуск всего расхода без их переполнения.

Расчёт подводящего канала сводится к определению нормальной и критической глубины, критического уклона, анализа состояния потока, определению средней скорости и обоснованию укрепления русла. Кроме этого необходимо привести расчёт гидравлически наивыгоднейшего профиля канала.

Определение нормальной глубины

Нормальная глубина 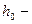это такая глубина, которая при заданном расходе установилась бы в русле, если в этом русле движение было бы равномерным.

Основная расчётная формула – формула Шези:

,

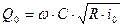(2.1)

где 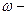площадь живого сечения, 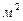; коэффициент Шези, ; 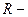гидравлический радиус, ; уклон канала.

Для трапецеидального сечения (рис. 2.1)

(2.2)

где глубина канала, .

 

Рис. 2.1.

Для определения коэффициента Шези может применятся формула Павловского:

(2.3.)

где .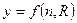

Приближенно можно считать:

При При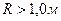

(2.4) (2.5)

Гидравлический радиус в общем случае определяется по формуле:

(2.6)

где смоченный периметр, , и для трапецеидального русла может быть определен:

(2.7)

Важным показателем при расчете является расходная характеристика (модуль расхода) :

(2.8)

Вычисление нормальной глубины буду проводить графоаналитическим методом.

Расчет

1) Определю необходимую расходную характеристику, соответствующую нормальной глубине :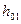

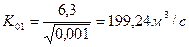
2) Задавая числовые значения произвольно выбранных глубин, я вычислю соответствующие расходные характеристики по формуле:

(2.9)

Для удобства расчет сведу в таблицу 2.1.

Таблица 2.1. Расчет расходных характеристик.

Расчетные формулы	Ед. изм.	Назначаемые и определяемые величины
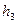
		0,50	0,7		1,50	1,7
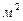
		1,12	1,78		5,62	6,88
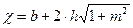
		3,30	4,02	5,10	6,90	7,62
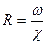
		0,34	0,44	0,58	0,81	0,90
		30,97	32,99	35,26	38,09	39,03
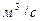
		20,31	39,21	81,08	193,37	255,32

 

3)Построю кривую по значениям глубин и соответствующих расходных характеристик.

Масштаб для построения графика выбираю следующий: для оси глубин в 1 см по вертикали вкладывается 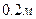(1:20), для оси расходных характеристик масштаб произвольный (рис. 2.2).

 

Рис. 2.2. График к определению .

3) Из графика видно что при числовом значении , величина нормальной глубины принимает следующие значение .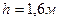

 

В качестве второго метода определения нормальной глубины применю метод профессора Б.А. Бахметова.

1) Задаю две произвольно выбранные глубины, 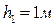, и вычислю для этих глубин 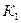, . Из таблицы 2.1 , .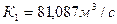

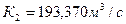2) Из соотношения:

 

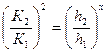
нахожу гидравлический показатель русла:

;

 

 

 

;

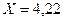
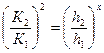если предположить что , то можно написать равенство:

 

;

задам значения: из таблицы 2.1 .

,

.

 

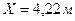
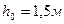Исходя из двух значени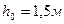й и принимаем .

 

Определение критической глубины.

Критической глубиной называется глубина, отвечающая минимуму удельной энергии сечения.

Если задано поперечное сечение русла, а также расход , то критическая глубина определяется из уравнения:

(2.10)

где удельная энергия сечения, , определяемая по формуле:

(2.11)

Для дорожно-мостового и аэродромного строительства при движении жидкости в каналах коэффициент Кариолиса принимают .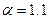

Дифференцируя выражение (2.11) по из условия при глубине, равной критической, получаем уравнение критического состояния потока:

(2.12)

где: ускорение свободного падения, .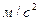

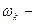площадь живого сечения при критической глубине, .

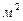ширина канала поверху при критической глубине, (рис. 2.3).

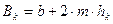
(2.13)

Рис. 2.3.

Для определения критической глубины буду использовать метод подбора.

Расчет

1) Из уравнения критического состояния потока при заданном расходе определю числовое значение величины ;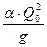

.

2) Задавая числовые значения произвольно выбранным глубинам, вычислю соответствующие значения . Для удобства расчет сведу в таблицу 2.2.

Таблица 2.2. Определение критической глубины.

0,5	1,125		0,47
0,7	1,785	3,6	1,60
1,0		4,5

3) Построю кривую . Масштаб для построения приму следующий: для оси глубин – 1:20, для оси в 1 см вкладывается 1 .

 

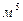Рис. 2.4. График к определению .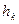

 

Из графика видно, что при , .

 

В качестве второго метода применю метод профессора И.И.Агроскина:

, где , q=4.2

φ (η)=0.35

1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: