 |
Кафедра математики и информатики
|
|
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И МОЛОДЕЖНОЙ ПОЛИТИКИ СТАВРОПОЛЬСКОГО КРАЯ
ГБОУ ВПО «СТАВРОПОЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ»
Психолого-педагогический факультет
Кафедра математики и информатики
КУРСОВАЯ РАБОТА
по дисциплине «Теоретические основы информатики»
на тему «Префиксный код Шеннона-Фано»
Профиль «Математика» и профиль «Информатика»
студента 2 курса
 Капниной Г.А.
Капниной Г.А.
Ф.И.О.
 |
подпись
Научный руководитель:
Красильников В.В., кандидат технических наук, доцент
Ф.И.О., уч. степень, звание
_______________________________________
подпись
Курсовая работа защищена с оценкой:_______
дата:__________________________________
Ставрополь, 2014
Содержание
Введение…………………………………………………………………………...3
1. Префиксный код Шеннона-Фано……………………………..……………….4
1.1 Кодирование……………………………………………………………4
1.2 Сжатие информации…………………………………………………...5
1.3 Префиксное кодирование …………………………..………………….7
1.4 Алгоритм Шеннона– Фано …………………………………………....8
1.5 Примеры решения задач……………...………………………………10
Выводы по первой главе………………………………………………………...15
2. Проект «………………………………………………………………..16
2.1 Основные положения метода проектов……………………..……16
2.2 Планирование учебного проекта…………………………………….17
2.3 Визитная карточка проекта…………………………………………..23
Выводы по второй главе…………………………………………………………
Приложение А Название ……………………………………………………..
Приложение Б…………………………………………………………………….
Введение
Необходимость кодирования информации возникла задолго до появления компьютеров. Речь, азбука и цифры - есть не что иное, как система моделирования мыслей, речевых звуков и числовой информации. В технике потребность кодирования возникла сразу после создания телеграфа, но особенно важной она стала с изобретением компьютеров.
|
|
|
Актуальность темы данной курсовой работы состоит в том, что с увеличением необходимости использования компьютера в различных областях, необходимо сжимать информацию для её более удобного и компактного хранения.
Какова же сущность префиксного кода Шеннона-Фано и как можно в рамках изучения школьного курса информатики доступно представить школьникам данную тему? В работе будет рассматриваться теоретическое обоснование алгоритма Шеннона-Фано и составлен проект, в рамках которого, школьники изучат этот вопрос.
Объектом исследования является процесс обучения информатики в старших классах средней общеобразовательной школы.
Предметом исследования - повышение уровня обучения за счет изучения дополнительного материала не входящего в планирование учебного предмета информатики.
Целью курсовой работы является доступное представление для школьников как теоретического, так и практического применения алгоритма
Шеннона-Фано.
Задачи:
- теоретически обосновать префиксный код Шеннона-Фано
- привести примеры решения задач
- разработать проект
- разработать визитную карточку проекта
- подготовить презентацию по проекту
- составить комплекс тестовых заданий по теоретической части курсовой работы
-сформулировать выводы по проделанной работе.
1. ПРЕФИКСНЫЙ КОД ШЕННОНА – ФАНО
1.1 Кодирование
Вся информация, которую хранит, обрабатывает и передает по сетям компьютер, представлена в виде двоичных чисел. Существуют международные стандарты и методы кодирования текстовой, числовой, изобразительной, звуковой и видеоинформации. Знание основных кодовых таблиц очень важно для правильного чтения информации Интернета, электронной почты, текстовых документов в кодировке различных операционных систем [1].
|
|
|
Думая о данных, обычно мы представляем себе ни что иное, как передаваемую этими данными информацию: список клиентов, мелодию на аудио компакт-диске, письмо и тому подобное. Как правило, мы не слишком задумываемся о физическом представлении данных. Заботу об этом - отображении списка клиентов, воспроизведении компакт-диска, печати письма - берет на себя программа, манипулирующая данными.
Для хранения в компьютере и передачи информации по каналам связи символы должны быть закодированы при помощи некоторого кодового алфавита - набора знаков, при помощи которых можно составлять слова.
С помощью двух цифр 0 и 1 можно закодировать любое сообщение. Это явилось причиной того, что в компьютере обязательно должно быть организованно два важных процесса [2]:
· Кодирование – преобразование входной информации в форму, воспринимаемую компьютером, т.е. двоичный код.
· Декодирование – преобразование данных из двоичного кода в форму, понятную человеку.
Код-это набор условных обозначений (или сигналов) для записи (или передачи) некоторых заранее определенных понятий.
Кодирование информации – это процесс формирования определенного представления информации. В более узком смысле под термином «кодирование» часто понимают переход от одной формы представления информации к другой, более удобной для хранения, передачи или обработки.
Человек кодирует информацию с помощью языка. Язык - это знаковая форма представления информации.[3]
Языки бывают естественные (русский, английский и т.д.) и формальные (язык математики, химии, программирования и т.д.) Любой язык имеет свой алфавит - набор основных символов, различимых по их начертанию. Алфавит обычно бывает жестко зафиксирован и имеет свой синтаксис и грамматику.
Одну и ту же информацию можно кодировать разными способами. Например, объект «КЛАВИАТУРА»: можно представить в виде текстовой информации - написать на русском языке и на английском. Можно представить в виде графической информации - фото и видео. Можно в виде звука - произнести это слово и т.д. Это разные способы кодирования одного и того же объекта.
|
|
|
Огромное количество различной информации неизбежно привело человека к попыткам создать универсальный язык или азбуку для кодирования. Эта проблема была реализована с помощью компьютера. Всю информацию, с которой работает компьютер, можно представить в виде последовательности всего двух знаков - 1 и 0. Эти два символа называются двоичным цифрами, по-английски - binary digit или бит.
Обычно каждый образ при кодировании представлении отдельным знаком. Знак - это элемент конечного множества отличных друг от друга элементов.
С точки зрения технической реализации использование двоичной системы счисления для кодирования информации оказалось намного более простым, чем применение других способов. Действительно, удобно кодировать информацию в виде последовательности нулей и единиц, если представить эти значения как два возможных устойчивых состояния электронного элемента: 0-отсутствие электрического сигнала;1-наличие электрического сигнала.
Эти состояния легко различать. Недостаток двоичного кодирования – длинные коды. Но в технике легче иметь дело с большим количеством простых элементов, чем с небольшим числом сложных.
1.2 Сжатие информации
Рассмотрим двойственность природы данных: с одной стороны, содержимое информации, а с другой - ее физическое представление. В 1950 году Клод Шеннон заложил основы теории информации, в том числе идею о том, что данные могут быть представлены определенным минимальным количеством битов. Эта величина получила название энтропии данных. Шеннон установил также, что обычно количество бит в физическом представлении данных превышает значение, определяемое их энтропией.
В качестве простого примера рассмотрим исследование понятия вероятности с помощью монеты. Можно было бы подбросить монету множество раз, построить большую таблицу результатов, а затем выполнить определенный статистический анализ этого большого набора данных с целью формулирования или доказательства какой-то теоремы. Для построения набора данных, результаты подбрасывания монеты можно было бы записывать несколькими различными способами: можно было бы записывать слова "орел" или "решка"; можно было бы записывать буквы "О" или "Р"; или же можно было бы записывать единственный бит (например "да" или "нет", в зависимости от того, на какую сторону падает монета). Согласно теории информации, результат каждого подбрасывания монеты можно закодировать единственным битом, поэтому последний приведенный вариант был бы наиболее эффективным с точки зрения объема памяти, необходимого для кодирования результатов. С этой точки зрения первый вариант является наиболее расточительным, поскольку для записи результата единственного подбрасывания монеты требовалось бы четыре или пять символов.
|
|
|
Однако посмотрим на это под другим углом: во всех приведенных примерах записи данных мы сохраняем одни и те же результаты - одну и ту же информацию - используя все меньший и меньший объем памяти. Другими словами, мы выполняем сжатие данных.
Сжатие сокращает объем пространства, требуемого для хранения файлов в ЭВМ, и количество времени, необходимого для передачи информации по каналу установленной ширины пропускания. Это есть форма кодирования.
Алгоритмы сжатия могут повышать эффективность хранения и передачи данных посредством сокращения количества их избыточности. Алгоритм сжатия берет в качестве входа текст источника и производит соответствующий ему сжатый текст, когда как разворачивающий алгоритм имеет на входе сжатый текст и получает из него на выходе первоначальный текст источника. Большинство алгоритмов сжатия рассматривают исходный текст как набор строк, состоящих из букв алфавита исходного текста.
В связи с непрерывным увеличением объема информации, накапливаемой во всех областях человеческой деятельности, все большее значение приобретают технологии ее компактного представления. Под компактным представлением информации следует понимать некоторую форму хранения информации, экономную с точки зрения занимаемого объема информационного носителя. Информационным носителем может являться любая физическая субстанция, будь то человеческий мозг, память вычислительной машины или простой лист бумаги.
Сжатие информации – это процесс преобразования информации, в результате которого необходим меньший объем памяти для её хранения, тем самым уменьшается избыточность информации.
Сжатие информации в файлах производится за счет устранения избыточности различными способами, например за счет упрощения кодов, исключения из них постоянных битов или представления повторяющихся символов в виде коэффициента повторения и соответствующих символов.
|
|
|
Суть любого алгоритма сжатия информации заключается в том, чтобы путем некоторого преобразования исходного набора информационных бит получить на выходе некоторый набор меньшего размера. Применяются различные алгоритмы подобного сжатия информации. Причем все алгоритмы преобразования данных можно условно разделить на два класса: обратимые и необратимые.
Под необратимым алгоритмом сжатия информации подразумевается такое преобразование исходной последовательности бит, при котором выходная последовательность меньшего размера не позволяет в точности восстановить входную последовательность. Алгоритмы необратимого сжатия используются, например, в отношении графических, видео и аудиоданных, причем это, всегда приводит к потере их качества.
Алгоритмы обратимого сжатия данных позволяют в точности восстановить исходную последовательность данных из сжатой последовательности. Именно такие алгоритмы и используются в архиваторах. Общими характеристиками всех алгоритмов сжатия являются степень, скорость и качество сжатия. Степень сжатия - отношение объема исходной к сжатой последовательности данных. Скорость сжатия - время, затрачиваемое на сжатие некоторого объема информации входного потока, до получения из него эквивалентного выходного. Качество сжатия - величина, показывающая, на сколько сильно упакован выходной поток, при помощи применения к нему повторного сжатия по этому же или иному алгоритму.
Существует немало различных методов сжатия, но есть некоторые принципы и правила, которые являются общими для всех методов сжатия:
1. У всякого сжатия есть предел. Уплотнение ранее уплотнённого файла или не даёт выигрыша или приводит к проигрышу.
2. Для всякого метода сжатия можно подобрать файл, применительно к которому данный метод является наилучшим. И наоборот: можно подобрать файл, который в результате сжатия не уменьшится, а увеличится.
Из вышесказанного следует, что программы – упаковщики до начала работы должны выполнять предварительный просмотр обрабатываемых файлов и выбирать тот метод упаковки, который даёт наилучший результат.
1.3 Префиксное кодирование
Префиксное кодирование основано на выработке систем кодов переменной длины, которые принято называть системами префиксных кодов (или кодов префикса). Особенность этих систем состоит в том, что в пределах каждой из них более короткие по длине коды не совпадают с началом (префиксом) более длинных кодов – так называемое свойство префикса.
Системы префиксных кодов обычно получают построением кодовых деревьев. Степень ветвления в этих деревьях зависит от основания системы представления информации. Рассмотрим случай двоичной системы представления, которой соответствуют бинарные кодовые деревья. Как известно, каждый внутренний узел бинарного дерева имеет до двух исходящих ребер. Пронумеруем эти ребра так, чтобы одному из них соответствовал двоичный символ «0», а другому – «1». Так как в дереве не может быть циклов, от корневого узла к листовому узлу всегда можно проложить единственный маршрут. Если ребра дерева пронумерованы, то каждому такому маршруту соответствует некоторая уникальная двоичная последовательность. Множество всех таких последовательностей, очевидно, образует систему префиксных кодов.
Первоначально каждому символу информационного алфавита ставится
в соответствие код нулевой длины («пустой» код) и вес, равный вероятности появления символа на выходе информационного источника в рамках выбранной информационной модели. Все символы алфавита сортируются по убыванию или возрастанию их весов, после чего упорядоченный ряд символов
в некотором месте делится на две части так, чтобы в каждой из них сумма весов символов была примерно одинакова. К кодам символов, принадлежащих одной из частей, добавляется «0», а к кодам символов, принадлежащим другой части, добавляется «1» (добавляемое значение формирует очередной крайний правый разряд кода). Как нетрудно понять, каждая из указанных частей сама по себе является упорядоченным рядом символов. Каждый из этих рядов, если он содержит более одного символа, в свою очередь делится на две части в соответствии с описанным выше принципом, и к кодам символов вновь добавляются соответствующие двоичные значения и т.д. Процесс завершается тогда, когда во всех полученных таким образом рядах остается ровно по одному символу.
Алгоритм Шеннона-Фано в действительности не строит кодовое дерево, однако его работу можно проиллюстрировать таким построением. При разделении группы символов происходит как бы разветвление некоторого узла бинарного дерева (листовой узел становится узлом родителем для двух новообразованных дочерних узлов), а присвоение нулей и единиц равносильно установлению соответствия между кодами и маршрутами движения по дереву от корневого узла к листовому узлу.
Префиксный код в теории кодирования – это код со словом переменной длины, удовлетворяющий условию Фано.
Условие Фано: неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом) какого-либо другого более длинного кода.
Например, если один из символов первичного алфавита имеет код «110», то в качестве кодов для других символов нельзя использовать последовательности «0» и «11», в тоже время последовательности «10» и «0» использовать можно (при условии что они не являются префиксом других кодов символов данного алфавита).
Декодирование префиксных кодов однозначно выполняется слева направо. При этом сопоставление с таблицей кодов всегда дает точное указание конца одного кода и начала следующего. Это дает возможность не использовать разделители.
1.4 Алгоритм Шеннона – Фано
Алгоритм Шеннона - Фано - один из первых алгоритмов сжатия. Он был разработан независимо друг от друга в 1948 году Клодом Элвудом Шенноном (публикация «Математическая теория связи») и, позже, Уго Фано (опубликовано как технический отчёт).
Алгоритм использует коды переменной длины: часто встречающийся символ кодируется кодом меньшей длины, редко встречающийся - кодом большей длины. Коды Шеннона - Фано префиксные, то есть никакое кодовое слово не является префиксом любого другого. Это свойство позволяет однозначно декодировать любую последовательность кодовых слов. Данный метод сжатия имеет большое сходство с алгоритмом Хаффмана, который появился на несколько лет позже. В отличие от алгоритма Шеннона - Фано, этот алгоритм остаётся всегда оптимальным и для вторичных алфавитов m2 с более чем двумя символами.
Кодирование Шеннона - Фано относится к вероятностным методам сжатия, точнее, методам контекстного моделирования нулевого порядка. Этот алгоритм использует избыточность сообщения, заключённую в неоднородном распределении частот символов его первичного алфавита, то есть заменяет коды более частых символов короткими двоичными последовательностями, а коды более редких символов - более длинными двоичными последовательностями.
Алгоритм представляет собой рекурсивную процедуру, позволяющую на основе заданного вероятностного распределения появления символов на выходе источника информации поэтапно формировать отвечающую ему систему префиксных кодов.
Алгоритм Шеннона-Фано работает следующим образом:
1. На вход приходят упорядоченные по невозрастанию частот данные.
2. Находится середина, которая делит алфавит примерно на две части. Эти части (суммы частот алфавита) примерно равны. Для левой части присваивается «1», для правой «0», таким образом мы получим листья дерева
3. повторяется до тех пор, пока мы не получим единственный элемент последовательности, т.е. листок
Алгоритм кодирования
1) Выписываются в ряд символы алфавита в порядке уменьшения их вероятности появления
2) Множество символов алфавита последовательно делятся на два подмножества, так чтобы сумма вероятностей появления символов одного подмножества была равна (или примерно равна) сумме вероятностей появления символов другого подмножества. Для первого подмножества, каждому символу припысывается код «0», а для второго – «1»
3) Разбиения на подмножества повторяются до тех пор, пока все не будут состоять из одного элемента.
Когда размер подалфавита становится равен нулю или единице, то дальнейшего удлинения префиксного кода для соответствующих ему символов первичного алфавита не происходит, таким образом, алгоритм присваивает различным символам префиксные коды разной длины. На шаге деления алфавита существует неоднозначность, так как разность суммарных вероятностей  может быть одинакова для двух вариантов разделения (учитывая, что все символы первичного алфавита имеют вероятность больше нуля).
может быть одинакова для двух вариантов разделения (учитывая, что все символы первичного алфавита имеют вероятность больше нуля).
1.5 Примеры решения задач
Код Шеннона - Фано строится с помощью дерева или таблицы. Построение этого дерева начинается от корня. Всё множество кодируемых элементов соответствует корню дерева. Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем. Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0.
При построении кода Шеннона - Фано разбиение множества элементов может быть произведено, вообще говоря, несколькими способами. Выбор разбиения на уровне n может ухудшить варианты разбиения на следующем уровне и привести к неоптимальности кода в целом. Другими словами, оптимальное поведение на каждом шаге пути ещё не гарантирует оптимальности всей совокупности действий. Поэтому код Шеннона - Фано не является оптимальным в общем смысле, хотя и дает оптимальные результаты при некоторых распределениях вероятностей. Для одного и того же распределения вероятностей можно построить, вообще говоря, несколько кодов Шеннон - Фано, и все они могут дать различные результаты. Если построить все возможные коды Шеннона - Фано для данного распределения вероятностей, то среди них будут находиться и все коды Хаффмана, то есть оптимальные коды.
Пример кодового дерева.
Исходные символы: A,B,C,D,E,F

Полученный код: A-11, B-101, C-100, D-00, E-011, F-010
Задача №1.
Пусть алфавит состоит из восьми символов, виды символов и их вероятности следующие: x1→1/4, x2→1/4, x3→1/8, x4→1/8, x5→1/16, x6→1/16, x7→1/16, x8→1/16.
Для построения кода целесообразно построить таблицу следующего вида (таблица «2»):
| x | P | код | ||||
| x1 | 1/4 | |||||
| x2 | 1/4 | |||||
| x3 | 1/8 | |||||
| x4 | 1/8 | |||||
| x5 | 1/16 | |||||
| x6 | 1/16 | |||||
| x7 | 1/16 | |||||
| x8 | 1/16 |
таблица «2».
Далее, следуя алгоритму, начинаем заполнять оставшиеся ячейки таблицы (таблица «3»)
| x | P | код | ||||
| x1 | ¼ | |||||
| x2 |  ¼ ¼
| |||||
 x3 x3
| 1/8 |  1 1
| ||||
| x4 | 1/8 | |||||
 x5 x5
| 1/16 |  1 1
| ||||
| x6 | 1/16 | |||||
| x7 | 1/16 |  1 1
| ||||
| x8 | 1/16 |  1 1
|
Таблица «3».
Полученные коды: x1→00
x1→01
x1→100
x1→101
x1→1100
x1→1101
x1→1110
x1→1111
Задача №2.
Пусть имеется первичный алфавит, состоящий из шести символов: {A; B; C; D; E; F}, также известны вероятности появления этих символов в сообщении, они равны соответственно 0,15; 0,2; 0,1; 0,3; 0,2; 0,05. Расположим эти символы в таблице 1 в порядке убывания их вероятностей.
| Первичный алфавит | D | B | E | A | C | F |
| Вероятность появления | 0,3 | 0,2 | 0,2 | 0,15 | 0,1 | 0,05 |
Таблица «1»
Кодирование осуществляется следующим образом. Все символы делятся на две группы с сохранением порядка следования (по убыванию вероятностей появления), так чтобы суммы вероятностей в каждой группе были приблизительно равны 38, а, следовательно, абсолютные разности суммарных
вероятностей каждой группы близки к нулю.
В нашем примере в первую группу попадают символы D и B, их суммарная вероятность использования равна 0,5), все остальные буквы, также имеющие суммарную вероятность появления 0,5 попадают во вторую группу. Поставим ноль в первый знак кодов для всех символов из первой группы, а первый знак кодов символов второй группы установим равным единице. Продолжим деление каждой группы. В первой группе два элемента, и деление на подгруппы здесь однозначно: в первой подгруппе будет символ D, а во второй - символ B. Во второй группе теоретически возможны два способа деления на подгруппы:
1) (Е) и (А, С, F)
2) (E, A) и (C, F)
3) (E, A, C) и (F)
В первом случае абсолютная разность суммарных вероятностей будет
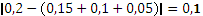
Во втором и третьем варианте деления аналогичные величины будут 0,2 и 0,4 соответственно.
Согласно алгоритму необходимо выбрать тот способ деления, при котором суммы вероятностей в каждой подгруппе были примерно одинаковыми, а, следовательно, вычисленная разность минимальна. Соответственно наилучшим способом деления будет следующий вариант: символ (E) остается в первой подгруппе, а символы (A, C, F) образуют вторую группу. Далее по имеющемуся алгоритму распределим нули и единицы в соответствующие знаки кода каждой подгруппы.
Осуществляем деление на подгруппы по той же схеме до тех пор, пока не получим группы, состоящие из одного элемента. Процедура деления изображена в нижеприведенной таблице (символ «-» означает, что данный знак кода отсутствует).
| Первичный алфавит | Вероятности появления символов | Знаки кода символа | Код символа | Длина кода | |||
| I | II | III | IV | ||||
| D | 0.3 | - | - | ||||
| B | 0.2 | - | - | ||||
| E | 0.2 | - | - | ||||
| A | 0.15 | - | |||||
| C | 0.1 | ||||||
| F | 0.05 |
Полученный код удовлетворяет условию Фано, следовательно, он является префиксным. Средняя длина этого кода равна:

Среднее количество информации на один символ первичного алфавита равно:
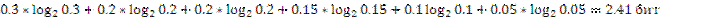
Теперь, найдем избыточность нашего алфавита:
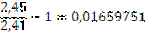
То есть избыточность кода Шеннона-Фано для нашего шестибуквенного алфавита составляет всего около 1,7 %. Для русского алфавита избыточность кодирования кодом Шеннона-Фано составила бы примерно 1,47%.
Задача №3.
Даны символы a, b, c, d с частотами  ;fb=0.25;
;fb=0.25;  ;
; 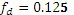 . Построить эффективный код методом Шеннона-Фано.
. Построить эффективный код методом Шеннона-Фано.
Сведем исходные данные в таблицу, упорядочив их по невозрастанию частот:
| Исходные символы | Частоты символов |
| a | 0.5 |
| b | 0.25 |
| c | 0.125 |
| d | 0.125 |
Первая линия деления проходит под символом a: соответствующие суммы Σ1 и Σ2 равны между собой и равны 0,5. Тогда формируемым кодовым комбинациям дописывается 1 для верхней (первой) части и 0 для нижней (второй) части. Поскольку это первый шаг формирования кода, двоичные цифры не дописываются, а только начинают формировать код.
| Исходные символы | Частоты символов | Формируемый код |
| a | 0.5 | |
| b | 0.25 | |
| c | 0.125 | |
| d | 0.125 |
В силу того, что верхняя часть списка содержит только один элемент (символ а), работа с ней заканчивается, а эффективный код для этого символа считается сформированным (в таблице, приведенной выше, эта часть списка частот символов выделена полужирным шрифтом).
Второе деление выполняется под символом b: суммы частот Σ1 и Σ2 вновь равны между собой и равны 0,25. Тогда кодовой комбинации символов верхней части дописывается 1, а нижней части – 0. Таким образом, к полученным на первом шаге фрагментам кода, равным 0, добавляются новые символы:
| Исходные символы | Частоты символов | Формируемый код |
| a | 0.5 | |
| b | 0.25 | |
| c | 0.125 | |
| d | 0.125 |
Поскольку верхняя часть нового списка содержит только один символ (b), формирование кода для него закончено (соответствующая строка таблицы вновь выделена полужирным шрифтом). Третье деление проходит между символами c и d: к кодовой комбинации символа c приписывается 1, коду символа d приписывается 0:
| Исходные символы | Частоты символов | Формируемый код |
| a | 0.5 | |
| b | 0.25 | |
| c | 0.125 | |
| d | 0.125 |
Поскольку обе оставшиеся половины исходного списка содержат по одному элементу, работа со списком в целом заканчивается.
Таким образом, получили коды:
а - 1, b - 01, c - 001, d - 000.
Определим эффективность построенного кода по формуле:
Icp = 0,5*1 + 0,25*2 + 0,125*3 + 0,125*3 = 1,75.
Поскольку при кодировании четырех символов кодом постоянной длины требуется два двоичных разряда, сэкономлено 0,25 двоичного разряда в среднем на один символ.
Кодирование Шеннона - Фано является достаточно старым методом сжатия, и на сегодняшний день оно не представляет особого практического интереса. В большинстве случаев, длина последовательности, сжатой по данному методу, равна длине сжатой последовательности с использованием кодирования Хаффмана. Но на некоторых последовательностях могут сформироваться неоптимальные коды Шеннона - Фано, поэтому более эффективным считается сжатие методом Хаффмана.
Выводы по первой главе:
· Кодирование информации является сложным, но необходимым процессом.
· Сжатие информации представляет собой операцию, в результате которой данному коду или сообщению ставится в соответствие более короткий код или сообщение.
· Алгоритмы сжатия информации бывают обратимыми и необратимыми.
· Префиксный код - код со словом переменной длины, имеющий такое свойство: если в код входит слово a, то для любой непустой строки b слова ab в коде не существует.
· Алгоритм использует коды переменной длины: часто встречающийся символ кодируется кодом меньшей длины, редко встречающийся -кодом большей длины.
· Коды Шеннона-Фано префиксные, то есть никакое кодовое слово не является префиксом любого другого.
· Для более подробного изучения и рассмотрения на практике алгоритма Шеннона-Фано необходимо разработать проект.
2. МЕТОД ПРОЕКТОВ
2.1 Сущность метода проектов
Метод проектов - это метод личностно-ориентированного обучения. Он развивает содержательную составляющую обучения, умения и навыки через комплекс заданий, способствующих актуализации исследовательской деятельности учащихся и аутентичным способам представления изученного материала в виде какой либо продукции или действий.
Метод проектов - это организационная модель образовательной деятельности, способствующая исследованию учащимися сложных проблем. Учебные проекты способствуют расширению возможностей обучения в классе и могут значительно отличаться друг от друга по предмету и области применения, а также могут выполняться учащимися широкого спектра возрастов. Проекты заставляют учащихся взять на себя определенную роль,
например:
· решающий проблему;
· принимающий решение;
· исследователь;
· документалист.
Проекты служат конкретным важным целям образования. Проекты не являются развлечением или дополнением к «настоящему» учебному плану или просто заданием по знакомой теме. Учебный план, реализуемый с использованием метода проектов, основан на важных вопросах, которые связывают содержательные стандарты и мышление высокого уровня с реальной целью. Учащиеся часто берут на себя роли из реальной жизни и выполняют значимые для них задания.
План изучения учебной темы, реализуемый с использованием метода проектов, базируется на важных вопросах, связывающих содержание образовательных стандартов с мыслительными умениями высокого уровня в рамках повседневного контекста
Преимущества проектного обучения:
· поощрение активного исследования и мышления на высоком уровне;
· возрастание уверенности учащихся в собственных силах и возможностях и улучшение отношения к учебе;
· в работе над проектами учащиеся берут на себя ответственность за собственное обучение более осмысленно по сравнению с традиционными методами учебной деятельности. В результате повышается качество обучения;
· усиливаются возможности развивать у учащихся обобщенные умения и способы деятельности, такие как мыслительные умения высокого уровня, видение и решение проблем, сотрудничество и общение;
· появляется более широкий спектр возможностей для обучения детей разного уровня развития, разных в культурном отношении.
Выделяют следующие характеристики эффективных учебных проектов:
· учащиеся находятся в центре процесса обучения, ведущей является деятельность учения;
· проект основан на проблеме, значимой для учащихся;
· проект фокусируется на важных целях и задачах обучения, ориентированных на образовательные стандарты;
· проект организуется вокруг направляющих вопросов;
· проект включает текущее формирующее оценивание и другие типы оценивания;
· проект содержит связанные между собой задачи, а деятельность в проекте ограничена временными рамками;
· проекты напрямую связаны с окружающим миром;
· учащиеся демонстрируют знания и умения через результаты (продукты) учебной деятельности или саму деятельность, которая организуется и осуществляется в ходе разработки самих продуктов;
· информационные технологии поддерживают и помогают повысить качество обучения;
· в работе над проектом развиваются и интегрируются мыслительные умения;
· различные методы обучения под
|
|
|


