 |
Дифференциал 1-го порядка сложной функции.
|
|
|
|
Определение производной. Ее физический и геометрический смысл.
 |
Пусть функция
 определена в точке
определена в точке 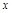 и в некоторой ее окрестности
и в некоторой ее окрестности 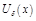 . Дадим аргументу
. Дадим аргументу 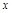 приращение
приращение 
 , тогда функция получит приращение
, тогда функция получит приращение 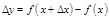 .
.
Опр. Производной функции 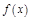 в т
в т 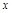 наз. предел отношения приращения функции к соответствующему приращению аргумента, когда последнее стремится к 0:
наз. предел отношения приращения функции к соответствующему приращению аргумента, когда последнее стремится к 0:
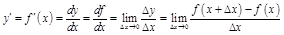 .
.
Пр. 


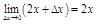 .
.
Опр. Правой (левой) производной наз. 
 .
.
Т1. (Критерий существования производной в точке)  существует
существует 
 и
и  . При этом
. При этом 
Опр. Функция 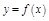 , имеющая конечную производную в точке
, имеющая конечную производную в точке 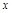 , наз. дифференцируемой в этой точке.
, наз. дифференцируемой в этой точке.
Опр. Если  , то говорят, что в точке
, то говорят, что в точке  существует бесконечная производная.
существует бесконечная производная.
Т.2. (О связи дифференцируемости и непрерывности функции в точке) Если ф-я 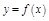 дифференцируема в точке
дифференцируема в точке  , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
Д-во:  , где
, где  – б.м. при
– б.м. при 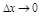 , тогда
, тогда 
 при
при 
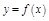 непрерывна.
непрерывна. 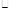
Зам. Дифференцируемость  непрерывность,
непрерывность,
непрерывность 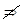 дифференцируемость.
дифференцируемость.
ПР.  – непрерывна на R, но не дифференцируема в точке
– непрерывна на R, но не дифференцируема в точке  , т.к.
, т.к.  .
.
 непрерывна на R, но не дифференцируема в точке
непрерывна на R, но не дифференцируема в точке  .
.
Геометрический смысл производной
Опр. Секущей называется прямая, соединяющая две точки графика функции 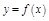 .
.
 Опр. Касательной к графику функции
Опр. Касательной к графику функции 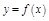 в точке
в точке 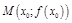 называется предельное положение
называется предельное положение  секущей
секущей  , когда точка
, когда точка  вдоль кривой (т.е. угол
вдоль кривой (т.е. угол 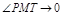 при
при  ).
).  ,
, 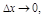
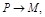

 ,
,  .
.
Замечание. 
 – угловой коэффициент касательной к графику функции
– угловой коэффициент касательной к графику функции 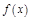 в
в 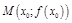 . Следовательно,
. Следовательно, 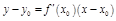 – уравнение касательной к графику функции
– уравнение касательной к графику функции 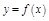 в точке
в точке  , где
, где  .
.
 ,
, 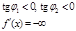 ,
, 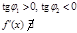 ,
,  .
.
Опр. Углом между кривыми наз. угол между касательными, проведенными к данным кривым в точке их пересечения.
Физический смысл производной.
Пусть точка движется по прямой, закон движения  . Дадим приращение
. Дадим приращение 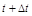 , тогда
, тогда  ,
, 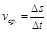 ,
, 
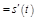 .
.
Правила дифференцирования
|
|
|
Опр. Операцию нахождения производной наз. операцией дифференцирования.
1) 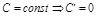 ,
,
Если функции  дифференцируемые в т.
дифференцируемые в т. 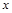 , то:
, то:
2)  ,
,
3)  ,
,
4) 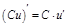 ,
,
5) 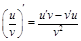 .
.
Д-во: 2) 


 .
.
3) 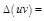


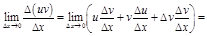
 .
.
5) 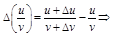


 .
.
1), 4) – доказать самостоятельно.
Таблица производных основных элементарных ф-й.
1.  2.
2. 
3.  4.
4. 
5. 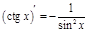 6.
6. 
7.  8.
8. 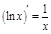
9. 
10.  11.
11. 
12.  13.
13. 
Докажем некоторые формулы из таблицы:
 .
.
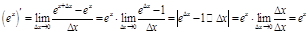 .
.
 .
.
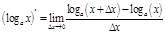
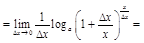 =
=  .
.
Производная сложной функции
Т.3. (О дифференцировании сложной функции) Если функция  дифференцируема в точке
дифференцируема в точке 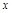 , а функция
, а функция 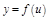 дифференцируема в точке
дифференцируема в точке  , то сложная функция
, то сложная функция  дифференцируема в точке
дифференцируема в точке 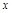 и
и  или
или  .
.
Д-во. Дадим аргументу 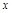 приращение
приращение  , тогда
, тогда  ,
, 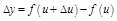 . Функция
. Функция 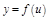 имеет производную в точке
имеет производную в точке  , следовательно,
, следовательно, 

 или
или  .
. 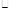
Следствие. Пусть 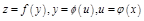 и существуют производные в соответствующих точках. Тогда
и существуют производные в соответствующих точках. Тогда  .
.
ПР.  ;
; 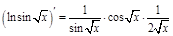 .
.
Дифференцирование обратной функции.
Опр. Функция называется строго возрастающей (убывающей) на промежутке  , если
, если 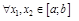
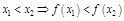
 .
.
Опр. Строго возрастающая или строго убывающая функция называется строго монотонной на  .
.
Т.4. (О производной обратной функции) Если функция 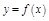 строго монотонна на интервале
строго монотонна на интервале 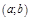 и имеет ненулевую производную
и имеет ненулевую производную 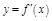 в некоторой т.
в некоторой т. 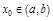 , то:
, то:
1)  обратная ф-я
обратная ф-я  ;
;
2)  в соответствующей точке
в соответствующей точке  ;
;
3)  или
или  .
.
Геометрическая интерпретация:

 ,
, 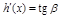
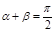

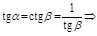
 .
.
Д-во. 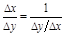 ;
; 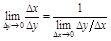 ; т.к
; т.к 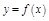 - дифференцируема.
- дифференцируема.  непрерывна
непрерывна 
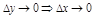 .
.
ПР.  ,
,  ,
, 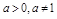 ;
; 
 .
.
ПР.  ,
,  ,
,  .
.
Дифференцирование функции, заданной параметрически
Т.5. (О производной параметрически заданной функции) Пусть 1) функция 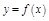 задана в виде
задана в виде  ;
;
2) функции 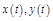 имеют производные в точке
имеют производные в точке  ;
;
3) для функции  существует обратная функция
существует обратная функция  и
и  дифференцируема в точке
дифференцируема в точке  . Тогда для функции
. Тогда для функции 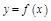 существует производная в точке
существует производная в точке 
 , т.е.
, т.е. 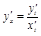 .
.
Д-во.  .
. 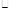
ПР.  Найти угол наклона касательной к оси Ох в точке, соответствующей значению
Найти угол наклона касательной к оси Ох в точке, соответствующей значению 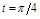 .
.
Решение. 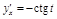 , т.е. при
, т.е. при 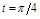 тангенс угла наклона касательной к графику данной функции
тангенс угла наклона касательной к графику данной функции 
 .
.
Дифференцирование функции, заданной неявно
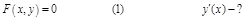
Правило дифференцирования неявной функции.
Чтобы найти производную неявно заданной функции, надо продифференцировать правую и левую части уравнения (1) как сложную функцию аргумента 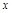 , помня, что
, помня, что 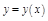 , и из полученного равенства найти
, и из полученного равенства найти  .
.
|
|
|
ПР. 
 .
.
Следствие. Логарифмическое дифференцирование:


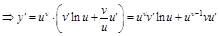 .
.
ПР.  …
…  .
.
Дифференциал функции
Т.6. (Необходимое и достаточное условие дифференцируемости функции в точке) Функция 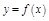 дифференцируема в точке
дифференцируема в точке 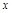 (т.е. имеет конечную производную) тогда и только тогда, когда ее приращение в этой точке можно представить в виде
(т.е. имеет конечную производную) тогда и только тогда, когда ее приращение в этой точке можно представить в виде 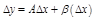 , где
, где  – б.м. более высокого порядка малости, чем
– б.м. более высокого порядка малости, чем  .
.
Д-во: 
 , тогда
, тогда  .
.

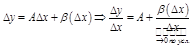

 .
. 
Пусть 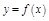 дифференцируема в точке x, т. е.
дифференцируема в точке x, т. е.  .
.
Опр. Дифференциалом функции 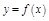 называется главная, линейная относительно
называется главная, линейная относительно  часть приращения функции:
часть приращения функции:  .
.
Замечание 1. Вообще говоря,  . Но для
. Но для 
 . В частности, для
. В частности, для  , т.е.
, т.е.  .
.
Замечание 2.  .
.
 Геометрический смысл дифференциала.
Геометрический смысл дифференциала.
Дифференциал функции в точке 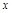 , соответствующий приращению
, соответствующий приращению  , есть приращение ординаты касательной к графику функции
, есть приращение ординаты касательной к графику функции 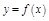 в точке с абсциссой
в точке с абсциссой 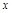 .
.
Свойства дифференциала:
1) 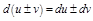 ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5) 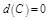 .
.
Замечание. В приближенных вычислениях используется, что 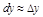 .
.
ПР.  ,
,  .
.
Дифференциал 1-го порядка сложной функции.
Инвариантность формы первого дифференциала
Пусть  ,
, 

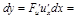
 , т.о. форма дифференциала не зависит от того, является ли аргумент функции независимой переменной или функцией другого аргумента (свойство инвариантности формы I-го дифференциала)
, т.о. форма дифференциала не зависит от того, является ли аргумент функции независимой переменной или функцией другого аргумента (свойство инвариантности формы I-го дифференциала)
|
|
|


