 |
Единственность обратной матрицы
|
|
|
|
В теории чисел наряду с числом 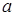 определяют число, противоположное ему (
определяют число, противоположное ему ( ) такое, что
) такое, что  , и число, обратное ему
, и число, обратное ему  такое, что
такое, что  . Например, для числа 5 противоположным будет число
. Например, для числа 5 противоположным будет число
(– 5), а обратным будет число  . Аналогично, в теории матриц мы уже ввели понятие противоположной матрицы, ее обозначение (– А). Обратной матрицей для квадратной матрицы А порядка n называется матрица
. Аналогично, в теории матриц мы уже ввели понятие противоположной матрицы, ее обозначение (– А). Обратной матрицей для квадратной матрицы А порядка n называется матрица  , если выполняются равенства
, если выполняются равенства

 , (1)
, (1)
где Е – единичная матрица порядка n.
Сразу же отметим, что обратная матрица существует только для квадратных невырожденных матриц.
Квадратная матрица называется невырожденной (неособенной), если det A ≠ 0. Если же det A = 0, то матрица А называется вырожденной (особенной).
Отметим, что невырожденная матрица А имеет единственную обратную матрицу  . Докажем это утверждение.
. Докажем это утверждение.
Пусть для матрицы А существует две обратные матрицы  ,
, 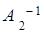 , то есть
, то есть

 и
и 
 .
.
Тогда  =
=  ּ
ּ 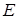 =
=  ּ(
ּ( ) =
) =
= ( ּ
ּ  )
) 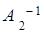 =
= 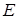
 =
= 
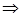
 =
=  .
.
Что и требовалось доказать.
Найдем определитель обратной матрицы. Так как определитель произведения двух матриц А и В одинакового порядка равен произведению определителей этих матриц, т. е.  , следовательно, произведение двух невырожденных матриц АВ есть невырожденная матрица.
, следовательно, произведение двух невырожденных матриц АВ есть невырожденная матрица.

 =
=  1
1 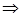
 .
.
Делаем вывод, что определитель обратной матрицы есть число, обратное определителю исходной матрицы.
АЛГОРИТМ ПОСТРОЕНИЯ ОБРАТНОЙ МАТРИЦЫ.
СВОЙСТВА ОБРАТНОЙ МАТРИЦЫ
Покажем, что, если матрица А невырожденная, то для нее существует обратная матрица, и построим ее.
Пусть
А =  ,
,  .
.
Составим матрицу из алгебраических дополнений элементов матрицы А:


Транспонируя ее, получим так называемую присоединенную матрицу:
|
|
|

 .
.
Найдем произведение  ּ
ּ  . С учетом теоремы Лапласа и теоремы аннулирования:
. С учетом теоремы Лапласа и теоремы аннулирования:
 ּ
ּ 
 =
=  =
=
= 
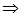
 .
.
Делаем вывод:
 . (2)
. (2)
Алгоритм построения обратной матрицы.
1)Вычислить определитель матрицы А. Если определитель равен нулю, то обратной матрицы не существует.
2)Если определитель матрицы не равен нулю, то составить из алгебраических дополнений соответствующих элементов матрицы А матрицу  .
.
3)Транспонируя матрицу  , получить присоединенную матрицу
, получить присоединенную матрицу 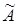 .
.
4)По формуле (2) составить обратную матрицу  .
.
5)По формуле (1) проверить вычисления.
Пример. Найти обратную матрицу.
а). Пусть А=  . Так как матрица А имеет две одинаковые строки, то определитель матрицы равен нулю. Следовательно, матрица вырожденная, и для нее не существует обратной матрицы.
. Так как матрица А имеет две одинаковые строки, то определитель матрицы равен нулю. Следовательно, матрица вырожденная, и для нее не существует обратной матрицы.
б). Пусть А = 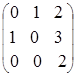 .
.
Вычислим определитель матрицы

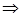 обратная матрица существует.
обратная матрица существует.
Составим матрицу из алгебраических дополнений
 =
= 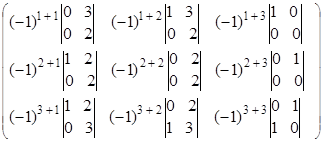 =
=  ;
;
транспонируя матрицу  , получим присоединенную матрицу
, получим присоединенную матрицу 

 ;
;
по формуле (2) найдем обратную матрицу 
 =
= 
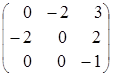 =
=  .
.
Проверим правильность вычислений

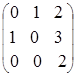
 =
=
=  =
=  .
.
Следовательно, обратная матрица построена верна.
Свойства обратной матрицы
1.  ;
;
2.  ;
;
3.  .
.
4. ЗАДАЧИ И УПРАЖНЕНИЯ 
4.1 Матрицы и действия над ними
1. Найти сумму, разность, произведения двух матриц А и В.
а)  ,
,  ;
;
б)  ,
,  ;
;
в) 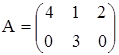 ,
, 
 ;
;
г) 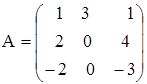 ,
,  ;
;
д)  ,
,  ;
;
е)  ,
,  ;
;
ж)  ,
,  ;
;
з)  ,
,  ;
;
и) 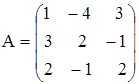 ,
,  .
.
2. Доказать, что матрицы А и В коммутирующие.
а)  ,
,  ; б)
; б)  ,
,  .
.
3. Даны матрицы А. В и С. Показать, что (АВ)·С=А·(ВС).
а) 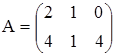 ,
,  ,
,  ;
;
б)  ,
,  ,
, 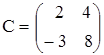 .
.
4. Вычислить (3А – 2В)·С, если
 ,
, 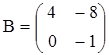 ,
,  .
.
5. Найти  , если
, если
а)  ; б)
; б)  .
.
6. Найти матрицу Х, если 3А+2Х=В, где
 ,
,  .
.
7. Найти АВС, если
а)  ,
,  ,
,  ;
;
б)  ,
,  ,
, 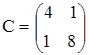 .
.
ОТВЕТЫ ПО ТЕМЕ «МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ»
1. а)  ,
, 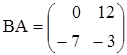 ;
;
б) произведения АВ и ВА не существуют;
|
|
|
в)  ,
,  ;
;
г)  ,
,  ;
;
д) суммы, разности и произведения ВА матриц не существуют,  ;
;
е)  ,
, 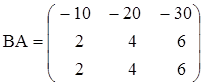 ;
;
ж) произведения матриц не существуют;
з)  ,
,  ;
;
и)  ,
,  .
.
2. а)  ; б)
; б)  .
.
3. а)  ; б)
; б)  .
.
4. 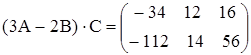 .
.
5. а) 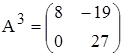 ; б)
; б)  .
.
6.  .
.
7. а)  ; б)
; б)  .
.
Определители
1. Вычислить определители
2.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ;
;
ж)  ; з)
; з)  .
.
3. С помощью правила треугольников вычислить определители
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
4. Вычислить определители примера 2, используя теорему Лапласа.
5. Вычислить определители, предварительно упростив их:
а) 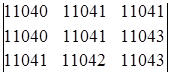 ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  ;
;
ж)  .
.
6. Вычислить определитель методом приведения его к треугольному виду
 .
.
7. Пусть даны матрицы А и В. Доказать, что  :
:
 ,
,  .
.
ОТВЕТЫ ПО ТЕМЕ «ОПРЕДЕЛИТЕЛИ»
1. а) 10; б) 1; в) 25; г) 16; д) 0; е) –3; ж) -6; з) 1.
2. а) –25; б) 168; в) 21; г) 12.
3. а) –25; б) 168; в) 21; г) 12.
4. а) 2; б) 0; в) 0; г) 70; д) 18; е) –66; ж) -36.
5. –24.
Обратная матрица
1. Найти обратную матрицу:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  ;
;
и)  ; к)
; к)  ; л)
; л)  ;
;
м)  ; н)
; н)  .
.
2. Найти обратную матрицу и проверить выполнение условия 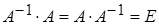 :
:
а)  ; б)
; б)  .
.
3. Доказать равенство  :
:
а)  ,
,  ; б)
; б)  ,
, 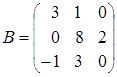 .
.
4. Доказать равенство  :
:
а)  ; б)
; б)  .
.
ОТВЕТЫ ПО ТЕМЕ «ОБРАТНАЯ МАТРИЦА»
1. а)  ; б)
; б) 
 ; в)
; в)  ; г)
; г) 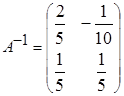 ;
;
д)  ; е)
; е)  ; ж)
; ж) 
 ;
;
з)  ; и)
; и)  ;
;
к)  ; л)
; л)  ;
;
м)  ; н)
; н)  .
.
2. а)  ; б)
; б)  .
.
2. а)  ,
,  ,
,  =
=  ;
;
б)  ,
,  ,
,
 =
=  .
.
5. а)  ,
,  ,
,
 ,
,  ;
;
б)  ,
,  ,
,
 ,
, 
 .
.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
1. Вычислить определитель разложением
а) по i- той строке;
б) по j- тому столбцу.
1.1. 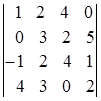 ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ;
;
i=2, j=3. i=4, j=1. i=3, j=2.
1.4.  ; 1.5.
; 1.5.  ; 1.6.
; 1.6.  ;
;
i=3, j=3. i=1, j=4. i=2, j=2.
1.7.  ; 1.8.
; 1.8.  ; 1.9.
; 1.9. 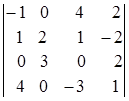 ;
;
i=4, j=4. i=2, j=2. i=3, j=2.
1.10.  ; 1.11.
; 1.11. 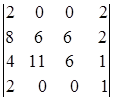 ; 1.12.
; 1.12.  ;
;
i=2, j=1. i=1, j=2. i=3, j=2.
1.13.  ; 1.14.
; 1.14.  ; 1.15.
; 1.15.  ;
;
i=2, j=3. i=1, j=3. i=4, j=2.
1.16.  ; 1.17.
; 1.17. 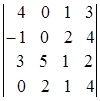 ; 1.18.
; 1.18.  ;
;
i=2, j=3. i=2, j=4. i=1, j=3.
1.19.  ; 1.20.
; 1.20. 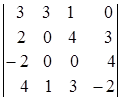 ; 1.21.
; 1.21.  ;
;
i=2, j=2. i=1, j=4. i=3, j=2.
1.22.  ; 1.23.
; 1.23.  ; 1.24.
; 1.24.  ;
;
i=1, j=3. i=2, j=1. i=3, j=4.
|
|
|
1.25.  ; 1.26.
; 1.26.  ; 1.27.
; 1.27.  ;
;
i=4, j=3. i=3, j=3. i=1, j=2.
1.28.  ; 1.29.
; 1.29.  ; 1.30.
; 1.30.  .
.
i=3, j=3. i=2, j=1. i=3, j=2.
ЛИТЕРАТУРА
1. Жевняк Р.М., Карпук А.А. Высшая математика. – Мн.: Выш. шк., 1992.- 384 с.
2. Гусак А.А. Справочное пособие к решению задач: аналитическая геометрия и линейная алгебра. – Мн.: Тетрасистемс, 1998.- 288 с.
3. Марков Л.Н., Размыслович Г.П. Высшая математика. Часть 1. –Мн.: Амалфея, 1999. – 208 с.
4. Белько И.В., Кузьмич К.К. Высшая математика для экономистов. I семестр. М.: Новое знание, 2002.- 140 с.
5.Коваленко Н.С., Минченков Ю.В., Овсеец М.И. Высшая математика. Учеб. пособие. -Мн.: ЧИУП, 2003. – 32 с.
|
|
|
12 |


