Методические указания по выполнению лабораторной работы

Задача изучения изменения анализируемых показателей во времени решается при помощи построения и анализа рядов динамики (временных рядов).

Ряд динамики (динамический ряд) представляет собой ряд числовых значений статистического показателя, расположенных в хронологической последовательности и характеризующих изменение социально-экономических явлений во времени.

В каждом ряду динамики имеются два основных элемента: уровни динамического ряда (обозначаются "Y") и период времени, за который они представлены ("t").

В зависимости от времени, отраженному в динамических рядах, они разделяются на моментные и интервальные.

Моментным рядом динамики называется такой ряд, уровни которого характеризуют состояние явления на определенную дату (момент) времени. Например, ряд, характеризующий динамику численности постоянного населения по состоянию на первое января каждого года.

Интервальным (периодическим) рядом динамики называется такой ряд, уровни которого характеризуют размер явления за конкретный период времени (год, месяц, квартал). Например, ряд, характеризующий динамику выпуска продукции за каждый месяц отчетного года.

Для количественной оценки динамики социально-экономических явлений применяется система показателей ряда динамики, которая может быть представлена следующей группой показателей: абсолютный прирост; темп (коэффициент) роста; темп (коэффициент) прироста; абсолютное значение одного процента прироста.

В основе расчета показателей рядов динамики лежит сопоставление его уровней. В зависимости от применяемого способа сопоставления (базисный или цепной) показатели динамики могут вычисляться на постоянной и переменной базах сравнения.

Для расчета показателей на постоянной базе (базисный способ расчета) каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называются базисными.

Для расчета показателей на переменной базе (цепной способ расчета) каждый последующий уровень ряда сравнивается с предыдущим. И показатели называются цепными.

Абсолютный прирост характеризует абсолютную скорость роста или снижения сравниваемых уровней, и рассчитывается как разность между последующим и предыдущим уровнем, принятым за базу сравнения. Измеряется в тех же единицах, что и исходная информация.

 

А = Y₁ - Y₀, (1)

 

где Y₁ - значение отчетного уровня ряда динамики;

Y₀ - значение базисного уровня ряда динамики.

Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т.е. общему приросту за весь промежуток времени.

Темп (коэффициент) роста характеризует относительную скорость роста или снижения уровней ряда динамики и представляет собой отношение каждого последующего уровня к предыдущему, принятому за базу сравнения. Темп роста измеряется в процентах, а коэффициент роста - в долях.

 

, (2), . (3)

 

Между цепными и базисными коэффициентами роста существует взаимосвязь: произведение последовательных цепных коэффициентов роста равно базисному темпу роста последнего периода; частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.

Темп (коэффициент) прироста показывает, на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения:

 

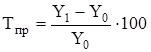, (4)

. (5)

 

Абсолютное значение одного процента прироста определяется отношением абсолютного прироста к темпу прироста, и показывает, сколько единиц в абсолютном выражении приходится на один процент прироста для данного ряда динамики. Расчет этого показателя целесообразен для цепного способа, для базисного способа он будет постоянной величиной:

 

. (6)

 

Для обобщающей характеристики динамики исследуемого явления за ряд периодов определяют различного рода средние показатели. Существуют две категории этих показателей:

1) средние уровни ряда;

2) средние показатели динамики данного ряда.

Метод расчета среднего уровня динамического ряда зависит от вида временного ряда.

В интервальных рядах динамики из абсолютных уровней средний уровень определяется по формуле средней арифметической:

простой (при равных интервалах):

 

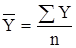, (7)

 

где 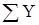 - сумма абсолютных уровней ряда;

n - число уровней.

взвешенной (при неравных интервалах):

 

, (8)

 

где Y - уровни ряда динамики, сохраняющиеся без изменения в течение промежутка времени t;

t - длительность интервалов времени (дней, месяцев) между смежными датами.

Для моментного ряда средний уровень определяется с помощью средней хронологической:

простой (для ряда динамики с равностоящими уровнями)

 

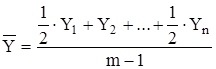, (9)

 

где Y - уровни периода, за который делается расчет;

m - число уровней.

взвешенной (для ряда динамики с неравностоящими уровнями):

 

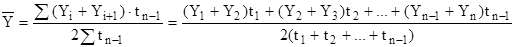, (10)

 

где Y_i, Y_n - уровни ряда динамики;

t - интервал времени между уровнями.

При определении средних уровней временного ряда нужно иметь в виду, что средняя будет достаточно надежной характеристикой ряда динамики, если она характеризует период с более или менее стабильными условиями развития. Если же за исследуемый период можно выделить этапы, в течение которых условия развития существенно менялись, то пользоваться общей средней не всегда целесообразно, а предпочтение нужно отдать средним, рассчитанным по отдельным периодам.

Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. При базисном способе расчета, чтобы определить средний абсолютный прирост, для этого определяется разность между конечным У_n и базисным У₀ уровнями изучаемого периода, которая делится на m-1 субпериодов:

 

, (11)

 

где m - число уровней ряда динамики в изучаемом периоде, включая базисный. При цепном способе расчета для определения среднего абсолютного прироста сумма цепных абсолютных приростов делится на их число:

 

, (12)

 

где n - число цепных абсолютных приростов в изучаемом периоде.

Средний темп (коэффициент) роста является обобщающей характеристикой индивидуальных темпов (коэффициентов) роста ряда динамики. Для базисного способа расчета средний темп (коэффициент) роста будет определяться по формуле:

 

, (13)

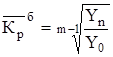. (14)

 

Для определения среднего темпа (коэффициента) роста цепным способом применяется формула средней геометрической:

 

100, (15)

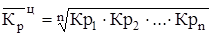, (16)

 

где К_р1, К_р2,..., К_рn - индивидуальные (цепные) коэффициенты роста;

n - число индивидуальных темпов роста

Средний темп (коэффициент) прироста рассчитывается на основе средних темпов (коэффициентов) роста по следующим формулам:

 

, (17), . (18)

 

Среднее значение одного процента прироста определяется только для цепного способа расчета по формуле:

 

. (19)

 

Данные показатели динамики находят практическое применение во всех расчетах, где требуется изучение изменения социально-экономических явлений во времени.

 

Поделиться:

Воспользуйтесь поиском по сайту: