 |
Полосы равной толщины. Кольца Ньютона. Интерферометры и их применение. Интерференционный микроскоп
|
|
|
|
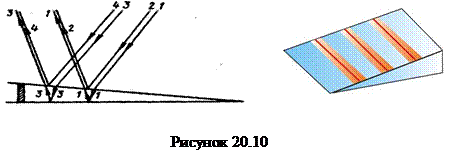 Интерференционные полосы в воздушном клине можно наблюдать, если положить одну плоскопараллельную стеклянную пластину на другую, а под один из концов верхней пластинки положить небольшой предмет таким образом, чтобы между ними образовался воздушный клин (рис. 20.10). В этом случае разность хода лучей определяется формулами (20.17) и (20.18). Допустим, что лучи 1-4падают на клин нормально (sinα = 0) и показатель преломления воздуха n =1, тогда
Интерференционные полосы в воздушном клине можно наблюдать, если положить одну плоскопараллельную стеклянную пластину на другую, а под один из концов верхней пластинки положить небольшой предмет таким образом, чтобы между ними образовался воздушный клин (рис. 20.10). В этом случае разность хода лучей определяется формулами (20.17) и (20.18). Допустим, что лучи 1-4падают на клин нормально (sinα = 0) и показатель преломления воздуха n =1, тогда
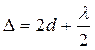 (20.19)
(20.19)
На границе, где стеклянные пластины соприкасаются, d ≈0 и Δ= λ/2 (20.10), поэтому наблюдается тёмная полоса (минимум).
Первая светлая полоса (k =1) возникает при Δ = λ, так как
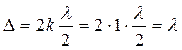 (20.20)
(20.20)
поэтому 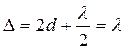 . Отсюда получим, что в этом месте толщина воздушного клина
. Отсюда получим, что в этом месте толщина воздушного клина  . Именно такой воздушный промежуток проходит параллельно грани соприкосновения, и светлая полоска имеет вид прямой линии.
. Именно такой воздушный промежуток проходит параллельно грани соприкосновения, и светлая полоска имеет вид прямой линии.
Вторая светлая полоса находится там, где толщина воздушного клина достигает значения 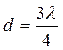 , так как при этом
, так как при этом 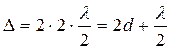
Эти полосы, каждой из которых соответствует своя вполне определенная толщина клина или параллельной пластинки, называют полосами равной толщины. Полосы равной толщины могут быть прямыми линиями, концентрическими окружностями и иметь любую другую форму в зависимости от расположения точек, соответствующих d = соnst. Угол клина должен быть очень малым, иначе полосы равной толщины ложатся друг на друга и их нельзя различить.
Полосы равной толщины можно получить, если положить плосковыпуклую линзу с большим радиусом кривизны (R = 10 + 100м) на плоскопараллельную пластинку (рис. 20.11, а). В этом случае полосы равной толщины имеют вид колец, которые называют кольцами Ньютона(рис. 20.11, б).
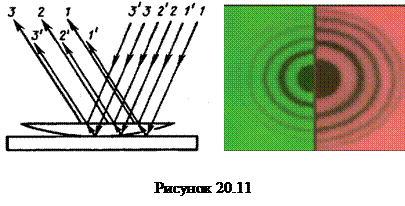 Если на линзу падает монохроматический свет, то волны, отраженные от верхней и нижней границ этой воздушной прослойки, интерферируют между собой и их разность хода зависит от толщины этого воздушного клина. В отраженном свете наблюдается следующая картина: в центре - черное пятно, окруженное чередующимися концентрическими светлыми и темными интерференционными кольцами убывающей ширины (рис. 20.11, б). В проходящем свете картина обратная: все светлые кольца заменяются темными, а в центре - светлое пятно.
Если на линзу падает монохроматический свет, то волны, отраженные от верхней и нижней границ этой воздушной прослойки, интерферируют между собой и их разность хода зависит от толщины этого воздушного клина. В отраженном свете наблюдается следующая картина: в центре - черное пятно, окруженное чередующимися концентрическими светлыми и темными интерференционными кольцами убывающей ширины (рис. 20.11, б). В проходящем свете картина обратная: все светлые кольца заменяются темными, а в центре - светлое пятно.
|
|
|
|
 такого просветления потери света из-за многократного отражения в сложных объективах могут достигать 70% и более. Для уменьшения этих потерь на каждую линзу наносят очень тонкую пленку (с показателем преломления, меньшим, чем у стекла) такой толщины, что световые волны, отраженные от ее передней и задней поверхностей, оказываются в противофазах и при интерференции гасят друг друга (рис.20.12). Гашение отраженного света ведет к увеличению доли энергии света, проходящего через оптическую систему, из-за чего ее и называют просветленной.
такого просветления потери света из-за многократного отражения в сложных объективах могут достигать 70% и более. Для уменьшения этих потерь на каждую линзу наносят очень тонкую пленку (с показателем преломления, меньшим, чем у стекла) такой толщины, что световые волны, отраженные от ее передней и задней поверхностей, оказываются в противофазах и при интерференции гасят друг друга (рис.20.12). Гашение отраженного света ведет к увеличению доли энергии света, проходящего через оптическую систему, из-за чего ее и называют просветленной.
Примеры решения задач.
Задача 1. В некоторую точку пространства приходят когерентные лучи с геометрической разностью хода l = 1,2 мкм, длина волны l которых в вакууме – 600 нм. Определить, что происходит в этой точке вследствие интерференции, когда лучи проходят в воздухе, воде и скипидаре. Показатель преломления воздуха n1 = 1, воды n2 = 1,33 и скипидара n3 = 1,5.
Решение.
| Дано | |
| l = 1,2×10-6 м | Оптическая разность хода 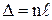
|
| l = 6×10-7 м | Для воздуха 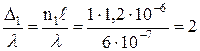
|
| n1 = 1 | |
| n2 = 1,33 | Для воды 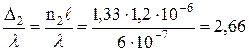
|
| n3 =1,5 | |
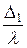 ; ; 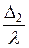 ; ; 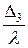
| Для скипидара 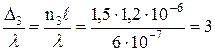
|
Условием интерференционного максимума является равенство оптической разности хода целому числу длин волн. Таким образом, в первом и третьем случае наблюдается усиление света, во втором – ослабление света.
|
|
|
Задача 2. В опыте с зеркалами Френеля расстояние между мнимыми изображениями источника света 0,5 мм, расстояние до экрана 5 м. В зеленом свете получились интерференционные полосы на расстоянии 5 мм друг от друга. Найти длину волны зеленого света.
Решение.
| Дано | |
| d = 0,5×10-3 м | Условие максимального усиления света 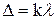
|
| L = 5 м | Расстояние между нулевым максимумом и максимумом k порядка 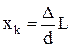
|
| XК = 5×10-3 м | |
| K = 1 | 
|
| l | При k = 1 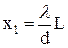 , отсюда , отсюда 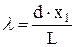
|
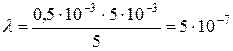 м.
м.
Задача 3. Какую наименьшую толщину должна иметь прозрачная пластинка, изготовленная из материала с показателем преломления 1,2, чтобы при освещении ее перпендикулярными лучами с длиной волны 600 нм она в отраженном свете казалась черной?
Решение.
| Дано | В отраженном свете оптическая разность хода |
| n = 1,2 | 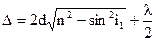
|
| i1 = 0 | Условие максимального ослабления света |
| l = 6×10-7 м | (пластина в отраженном свете будет казаться черной) |
| dmin | 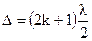
|
Т.к. i1 = 0, имеем
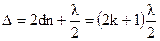

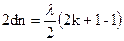 ;
; 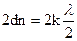 ;
;
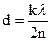
Наименьшая толщина пластин должна быть при k = 1, тогда
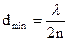 ;
; 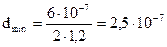 м = 250 нм.
м = 250 нм.
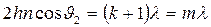
|
|
|


