Задача 4. Система Гордина. Отрезки касательных, проведенных из одной точки. Сложность 3.

Геометрия

Теория:

Ø Угол между касательной и хордой равен вписанному углу опирающемуся на эту хорду;

Ø Вписанный четырехугольник: суммы противоположных углов равны;

Ø Четыре точки на одной окружности: отрезок виден под одним и тем углом из двух других точек;

Ø Признаки параллельности прямых: накрест лежащие, односторонние, соответственные

Ø Медиана, проведенная к гипотенузе равна ее половине;

Ø Длины общих касательных к двум окружностям равны;

Ø Параллельные касательные расположены расстоянии диаметра.

Рекомендации

Ø Проводить касательные, хорды и другие дополнительные построения;

Ø Делать роспись углов;

Ø Заменять равные величины;

Ø Читать теорию

Ø Делать несколько рисунков

 

Задача 1. Угол между касательной и хордой. Четырехугольник KLNM – вписанный, A – точка пересечения диагоналей. RA – касательная к окружности, описанной около треугольника KLA. Доказать, что MN параллельна RA.

Задача 2. Угол между касательной и хордой. Треугольник ABC – вписанный (O – центр окружности). На продолжении сторон AC и BC за точку C взяты точки M и N, соответственно, так чтобы угол BAM равен углу CNM. Доказать что, прямая OC перпендикулярна MN.

Задача 3. KLMN – вписан в окружность с центром O (O внутри). Углы KON и LNM равны 100 и 40, градусам, соответственно. Доказать, что KM перпендикулярно LN.

Задача 4. Отрезки касательных, проведенных из одной точки. В треугольник KLM (стороны k, l, m) вписана окружность. А – точка касания окружности и стороны LM. Найдите LA и AM.

Задача 5. Отрезки касательных, проведенных из одной точки. В треугольник KLM (стороны k, l, m) вписана окружность. А – точка касания окружности и стороны LM. G – точка касания вневписанной окружности и стороны LM. Найдите LG, GA и AM.

Задача 6. Центр O окружности w ₁ лежит на окружности w₂. L и K – точки пересечения данных окружностей. Точка M лежит на окружности w₁ так, что ML – касательная к окружности w₂. A) Докажите, что KL = ML. Б) Найдите угол между прямыми LO и KM.

Задача 7. Точки –основания высот остроугольного треугольника KLM. Известно, что в треугольнике две стороны параллельны сторонам треугольника KLM. Докажите, что треугольник KLM - равносторонний.

Задача 8. LP – биссектриса тупого угла равнобедренной трапеции KLMN, описанной около окружности (P лежит на KN). Докажите, что площадь треугольника KLP равна площади четырехугольника LMNP.

Задача 9. Теорема Фалеса. На катете ML прямоугольного треугольника KLM (угол L – прямой) как на диаметре во внешнюю сторону построена полуокружность, точка S – середина этой полуокружности. В каком отношении прямая KS делит биссектрису LE треугольника KLM?

Задача 10. На стороне KM треугольника KLM (со сторонами k, l, m) выбрана точка N. B треугольники KLN и MLN вписаны окружности, и к ним проведена общая внешняя касательная (отличная от KM), пересекающая LN в точке Q. Найдите длину отрезка LQ.

Задача 11. Пусть Q – точка пересечения диагоналей параллелограмма KLMN. Окружность, проходящая через точки K, L, Q касается прямой LM. Докажите, что окружность, проходящая через точки L, Q, M, касается прямой MN.

Задача 12. Окружности w1 и w2 пересекаются в точках K и L. Равнобедренный треугольник MNL (LN -основание) – вписан в окружность w2. Отрезок ML (или его продолжение) пересекает окружность w1 в точке Q, а продолжение отрезка MK (или сам отрезок MK) пересекает окружность w1 в точке P. Доказать, что PQ параллельно LN.

Задача 13. На боковой стороне KL (KL = LM) равнобедренного треугольнике KLM выбрана точка P, и вокруг треугольников KPM и PLM описаны окружности w₁ и w₂ соответственно. Касательная, проведённая к w₁ в точке P, пересекает второй раз окружность w₂ в точке Q. Докажите, что LQ || KM.

Задача 14. KL - общая внешняя касательная к окружностям w₁и w₂ (K и L – точки касания). Кроме того, окружности w₁ и w₂касаются внешним образом в точке O. Прямая, параллельная прямой KL, касается w₂в точке Nи пересекает w₁в двух точках. Докажите, что точки K, Oи Nлежат на одной прямой.

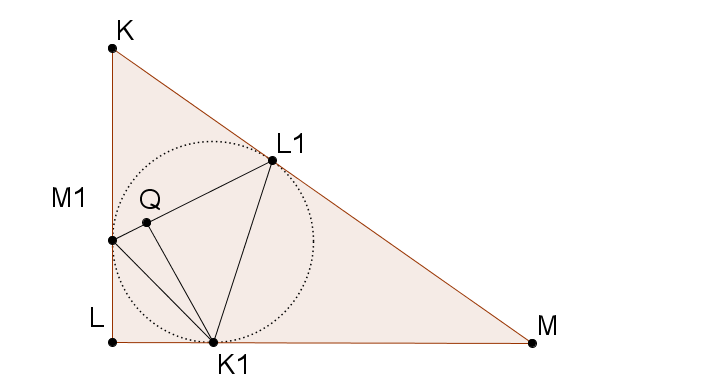
Задача 15. В прямоугольный треугольник KLM с гипотенузой MK вписана окружность, которая касается его сторон KL, LM, KM в точках 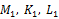соответственно. Пусть K1Q – высота треугольника . Найдите угол .

Решения

Задача 1. Угол между касательной и хордой. Сложность 2+

Четырехугольник KLNM – вписанный, A – точка пересечения диагоналей. RA – касательная к окружности, описанной около треугольника KLA. Доказать, что MN параллельна RA.
Решение: Московская устная олимпиада по геометрии, 2006, 8-9 кл, Заславский А.А

Угол между проведённой касательной RA и хордой LA равен вписанному углу LKA (см. рис.). Kроме того, ∠MNL = ∠LKM = ∠RAL. Tаким образом, ∠RAL = ∠MNA, следовательно, MN || RA.

Задача 2. Угол между касательной и хордой. Сложность 3+

Треугольник ABC – вписанный (O – центр окружности). На продолжении сторон AC и BC за точку C взяты точки M и N, соответственно, так чтобы угол BAM равен углу CNM. Доказать что, прямая OC перпендикулярна MN.

Решение. Точки A,B,M,N лежат на одной окружности (по признаку). Проведем в точке C касательную LC к окружности O. Тогда угол BCL равен углу BAC, а значит, равен углу BNM. Поэтому, LC параллельна MN. Следовательно, NM перпендикулярно радиусу OC.

Задача 3. Вписанный угол равен половине центрального. Сложность 2+.

KLMN – вписан в окружность с центром O (O внутри). Углы KON и LNM равны 100 и 40, градусам, соответственно. Доказать, что KM перпендикулярно LN.

Решение: Оригинал: Заславский А.А., Всеросс олимп по геом, 2005, 9 кл.

Угол KON – центральный, значит угол KMN равен 50 градусам. Пусть Q – точка пересечения диагоналей. Рассмотрим треугольник QMN. Угол MQN равен 180 – 50 – 40 = 90.

Задача 4. Система Гордина. Отрезки касательных, проведенных из одной точки. Сложность 3.

В треугольник KLM (стороны k, l, m) вписана окружность. А – точка касания окружности и стороны LM. Найдите LA и AM.

Решение. Обозначим точки касания на сторонах KL и KM через B и С соответственно. Тогда m = KB+BL = KC+ AL = l-CM + k-AM = l-AM+k-AM, отсюда AM = (l+k-m)/2. Значит, LA = k – (l+k-m)/2 = (k+m-l)/2.

Задача 5. Отрезки касательных, проведенных из одной точки. Вневписанная окружность. Сложность 3+.

В треугольник KLM (стороны k, l, m) вписана окружность. А – точка касания окружности и стороны LM. G – точка касания вневписанной окружности и стороны LM. Найдите LG, GA и AM.

Решение.

Пусть B и C — точки касания вписанной окружности со сторонами KL и KM соответственно. Тогда m = KB + BL = KC + L A = l - CM + k - AM = l - AM + k - AM. Поэтому CM = ½ (l+k-m). Далее, пусть P и Q - точки касания продолжений сторон KL и KM со вневписанной окружностью. Тогда KP = KQ. Значит, m+LP = l+MQ, m+LG=l+MG, m+LG=l+k-LG. Поэтому LG=1/2(l+k-m). 3. AG = k-AM-LG = m-l.

Задача 6

Центр O окружности w ₁ лежит на окружности w₂. L и K – точки пересечения данных окружностей. Точка M лежит на окружности w1 так, что ML – касательная к окружности w2. A) Докажите, что KL = ML. Б) Найдите угол между прямыми LO и KM.

Решение. Просолов В.В. Турнир городов 1991/1992, 8-9. Угол между касательной и хордой. Сложность 2+.

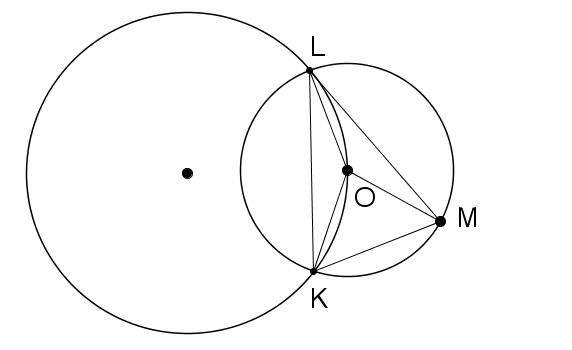
Отрезки OL, OK и OM равны как радиусы одной окружности. ∠ LKO = ∠ MLO по теореме об угле между касательной и хордой. Поэтому равнобедренные треугольники KOL и LOM равны Следовательно, KL = ML. Значит, треугольник KLM – равнобедренный. LO – биссектриса, так как треугольник KOL – равнобедренный. Следовательно, LO – высота, поэтому прямая перпендикулярна к основанию KM.

Задача 7

Точки K_1L_1M_1 –основания высот остроугольного треугольника KLM. Известно, что в треугольнике K_1L_1M_1 две стороны параллельны сторонам треугольника KLM. Докажите, что треугольник KLM - равносторонний.

Решение. Система Гордина. Турнир городов 1986/1988, 7-8 кл. Четыре точки на окружности; медиана, проведенная к гипотенузе; вписанная трапеция. Сложность 2+.

Точки L₁ и M ₁ лежат на окружности с диаметром LM (доказать!). Поэтому M L_ 1M_1L – вписанная трапеция, значит, она равнобедренная, то есть ∠ M = ∠L. Аналогично доказывается равенство других двух углов. Таким образом, треугольник KLM – равносторонний.

Задача 8

LP – биссектриса тупого угла равнобедренной трапеции KLMN, описанной около окружности (P лежит на KN). Докажите, что площадь треугольника KLP равна площади четырехугольника LMNP.

Решение. Турнир городов 2010/2011, 8-9 кл. Вписанная окружность. Замена равных величин. Сложность 3.

Пусть A,B – точки касания окружности с основаниями LM и KN, соответственно, O – центр окружности. Тогда AB делит площадь трапеции KLMN пополам. Покажем, что площади треугольников LAO, PBO равны. Действительно, AB – диаметр, поэтому AO=OB; углы LOA и POB – вертикальные. Далее остается заменить данные треугольники.

Задача 9

На катете ML прямоугольного треугольника KLM (угол L – прямой) как на диаметре во внешнюю сторону построена полуокружность, точка S – середина этой полуокружности. В каком отношении прямая KS делит биссектрису LE треугольника KLM?

Решение. Гордин Р.К. Турнир городов, 2013/2014, 8-9 кл. Угол опирающийся на диаметр; теорема Фалеса. Сложность 3+.

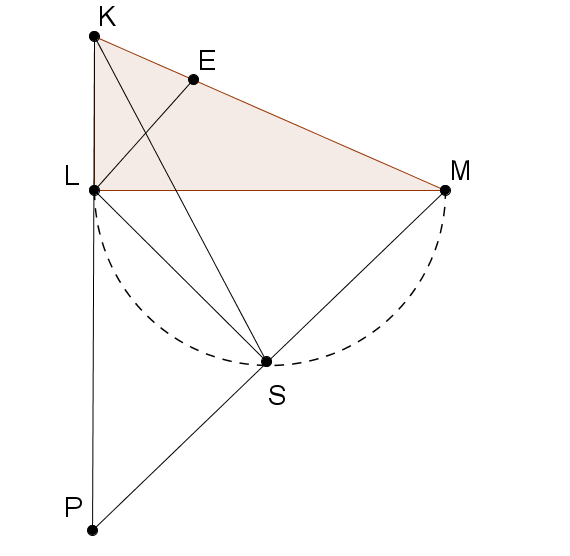
Продлим отрезок MS до пересечения с прямой KL в точке P. В треугольнике PML высота LS является и биссектрисой, поэтому PS = MS. Углы K LE и LPM равны 45°, то есть LE || MP. Значит, в треугольнике PKM медиана KS делит пополам и LE.

Задача 10

На стороне KM треугольника KLM (со сторонами k,l,m) выбрана точка N. B треугольники KLN и MLN вписаны окружности, и к ним проведена общая внешняя касательная (отличная от KM), пересекающая LN в точке Q. Найдите длину отрезка LQ.

Решение. Шарыгин И.Ф. Московская математическая олимпиада, 1994, 8-9. Отрезки касательных; длина общей касательной. Сложность 3+

Обозначим точки касания, как показано на рисунке.

Заметим, что AB ₁ = AP, AC ₁ = AQ, KM = KP, KN = KQ. Кроме того, MN = EF – отрезки общих касательных к окружностям. Поэтому
2 AK = (AP – KP) + (AQ – KQ) = AP + AQ – MN = AB ₁ + AC ₁ – EF = AB – BB ₁ + AC – CC ₁ – (BC – BE – CF) = AB + AC – BC.

Задача 11

Пусть Q – точка пересечения диагоналей параллелограмма KLMN. Окружность, проходящая через точки K, L, Q касается прямой LM. Докажите, что окружность, проходящая через точки L, Q, M, касается прямой MN.

Решение. Заславский А.А. Турнир городов 1998/1999, Московская математическая олимпиада 1999, 8-9 кл. Угол между касательной и хордой. Сложность 3.

Из теоремы об угле между касательной хордой следует, что ∠MLQ = ∠LKQ = ∠QMN = ∠MLQ. По теореме, обратной теореме об угле между касательной и хордой, NM – касательная к окружности, проходящей через точки L, Q, M.

Задача 12

Окружности w1 и w2 пересекаются в точках K и L. Равнобедренный треугольник MNL (LN -основание) – вписан в окружность w2. Отрезок ML (или его продолжение) пересекает окружность w1 в точке Q, а продолжение отрезка MK (или сам отрезок MK) пересекает окружность w1 в точке P. Доказать, что PQ параллельно LN.

Решение. Женодаров Р.Г. Всеросс, РЭ, 2010/2011, 9 кл. Углы, опирающиеся на одну дугу; четыре точки на окружности; смежные углы. Сложность 3.

∠MLN = ∠MNL = ∠PKL = ∠PQL, значит, прямые PQ и LN параллельны.

Задача 13

На боковой стороне KL (KL = LM) равнобедренного треугольнике KLM выбрана точка P, и вокруг треугольников KPM и PLM описаны окружности w₁ и w₂ соответственно. Касательная, проведённая к w₁ в точке P, пересекает второй раз окружность w₂ в точке Q. Докажите, что LQ || KM.

Решение:

∠QLM = ∠QPM = ∠PKM = ∠KML = ∠MLQ. Следовательно, LQ || KM.

 

Задача 14

KL - общая внешняя касательная к окружностям w1и w2 (K и L – точки касания). Кроме того, окружности w1 и w2касаются внешним образом в точке O. Прямая, параллельная прямой KL, касается w2в точке Nи пересекает w1в двух точках. Докажите, что точки K, Oи Nлежат на одной прямой.

Решение. Система Гордина, 8-9 кл. Общая касательная; отрезки касательных. Сложность 3.

 

Так как касательные к окружности w ₂ в точках Lи Nпараллельны, то LN– ее диаметр, и LON= 90 ^o. Докажем, что и LOK= 90 ^o. Проведем через точку Oобщую касательную к окружностям (рис), пусть она пересекает прямую KL в точке M. Из равенства отрезков касательных, проведенных к окружности из одной точки, следует, что треугольники KMO и LMOравнобедренные. Следовательно, KOL= KOM+ MOL= MKO+ MLO= 90 ^o.

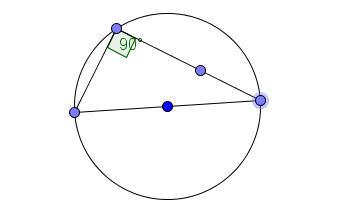
Задача 15

В прямоугольный треугольник KLM с гипотенузой MK вписана окружность, которая касается его сторон KL, LM, KM в точках M1, K1, L1 соответственно. Пусть K1Q – высота треугольника K1L1M1. Найдите угол L1K1Q.

Решение:

Угол LK1M1 равен 45 градусам. Следовательно угол K1L1Q равен 45 градусам (угол между касательной и хордой), поэтому ∠L1K1Q = 45°.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: