 |
Площадь криволинейной трапеции.
|
|
|
|
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
1. Площадь криволинейной трапеции.
2. Длина дуги кривой.
3. Площадь поверхности вращения
4. Объем пространственного тела.
Площадь криволинейной трапеции.
Теорема 1. Если функция 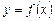 неотрицательна и непрерывна на отрезке
неотрицательна и непрерывна на отрезке  , то площадь криволинейной трапеции
, то площадь криволинейной трапеции
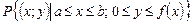
вычисляется по формуле  .
.
► Пусть
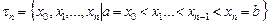
разбиение отрезка  .
.
И пусть 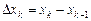 – длина частичного отрезка
– длина частичного отрезка 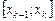 ,
,  . На каждом таком отрезке произвольным образом выберем точку
. На каждом таком отрезке произвольным образом выберем точку  . Тогда значение функции
. Тогда значение функции 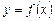 в точке
в точке  равно
равно  . Построим прямоугольники, основанием которых являются отрезки
. Построим прямоугольники, основанием которых являются отрезки 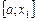 ,
,  ,
,  ,
, 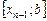 , а высота равна
, а высота равна  .
. 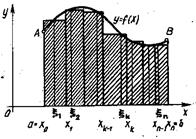
Рис.1. Площадь криволинейной трапеции
Площадь каждого прямоугольника равна 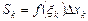 . Сумма
. Сумма  представляет собой площадь заштрихованной ступенчатой фигуры, изображенной на рисунке 1.
представляет собой площадь заштрихованной ступенчатой фигуры, изображенной на рисунке 1.
Эта площадь зависит от разбиения  отрезка
отрезка  на частичные отрезки и выбора точек
на частичные отрезки и выбора точек  . Чем меньше
. Чем меньше 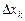 ,
,  , тем площадь ступенчатой фигуры ближе к площади криволинейной трапеции. Поэтому
, тем площадь ступенчатой фигуры ближе к площади криволинейной трапеции. Поэтому  . Точное значение площади
. Точное значение площади  криволинейной трапеции получается при
криволинейной трапеции получается при  :
:
 ,
,
где  . ◄
. ◄
Замечания. 1. Если 
 , то и
, то и  ,
,  . Следовательно, в этом случае
. Следовательно, в этом случае
 .
.
2. Если подынтегральная функция  конечное число раз меняет знак на отрезке
конечное число раз меняет знак на отрезке  , то интеграл
, то интеграл  равен алгебраической сумме площадей соответствующих криволинейных трапеций, лежащих над осью Ох (со знаком «+») и под этой осью (со знаком «–») (рис.2). Для того чтобы получить общую площадь заштрихованной фигуры, отрезок интегрирования
равен алгебраической сумме площадей соответствующих криволинейных трапеций, лежащих над осью Ох (со знаком «+») и под этой осью (со знаком «–») (рис.2). Для того чтобы получить общую площадь заштрихованной фигуры, отрезок интегрирования  надо разбить на частичные отрезки, на которых функция
надо разбить на частичные отрезки, на которых функция  сохраняет знак, и вычислить площади. Тогда
сохраняет знак, и вычислить площади. Тогда
 .
.
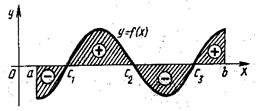
Рис.2. Площадь криволинейной трапеции
3. Если надо вычислить площадь фигуры, ограниченной линиями  ,
,  ,
,  ,
,  , то эту площадь рассматривают как разность площадей двух криволинейных трапеций
, то эту площадь рассматривают как разность площадей двух криволинейных трапеций  и
и  (рис.4). В этом случае можно воспользоваться одной из формул:
(рис.4). В этом случае можно воспользоваться одной из формул:
|
|
|
 , если
, если 
 (рис.3, а),
(рис.3, а),
 , если
, если 
 (рис.3, б).
(рис.3, б).
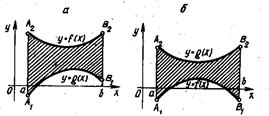
Рис.3. Площадь криволинейной трапеции
В случае, когда разность  не сохраняет знак на отрезке
не сохраняет знак на отрезке  ,этот отрезок разбивают на частичные отрезки, на каждом из которых функция
,этот отрезок разбивают на частичные отрезки, на каждом из которых функция  сохраняет знак. Например, для случая, изображенного на рис.5, площадь заштрихованной фигуры находится по формуле
сохраняет знак. Например, для случая, изображенного на рис.5, площадь заштрихованной фигуры находится по формуле
 .
.
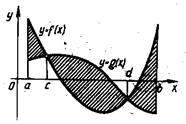
Рис.4. Площадь криволинейной трапеции
Пример. Вычислить площадь фигуры, ограниченной аркой синусоиды  .
.
Решение. Имеем
 .
.
В параметрическом виде.Если криволинейная трапеция ограничена линией, заданной уравнениями в параметрической форме  ,
,  , где
, где  , осью Ох и прямыми
, осью Ох и прямыми  ,
,  , причем
, причем  ,
,  , то ее площадь
, то ее площадь  при
при  вычисляется по формуле
вычисляется по формуле
 ,
,
которая получается заменой переменной  ,
,  ,
,  . Пределы
. Пределы  ,
, 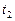 определяют из уравнений
определяют из уравнений  ,
,  .
.
Пример. Вычислить площадь эллипса
 ,
,
где  .
.
Решение. Оси координат совпадают с осями симметрии данного эллипса и поэтому делят его на четыре одинаковые части. Следовательно,
 ,
,
где 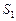 – площадь части эллипса, расположенная в первом квадранте. Тогда
– площадь части эллипса, расположенная в первом квадранте. Тогда
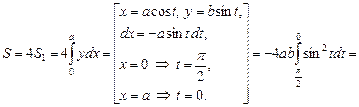
 .
.
В полярной системе координат.Пусть фигура, ограниченная линией  , заданной в полярной системе координат
, заданной в полярной системе координат  уравнением
уравнением 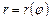 ,
,  .
.
Криволинейным сектором называется фигура, ограниченная линией 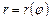 и радиусами-векторами
и радиусами-векторами  ,
,  (рис.5).
(рис.5).
При этом криволинейный сектор является правильной фигурой, если любой луч  ,
,  , исходящий из полюса
, исходящий из полюса  , пересекает линию
, пересекает линию 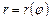 не более чем в одной точке. И пусть функция
не более чем в одной точке. И пусть функция 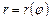 непрерывна на отрезке
непрерывна на отрезке  .
.
 Рис.5. Криволинейный сектор
Рис.5. Криволинейный сектор
|  Рис.6. Разбиение криволинейного сектора
Рис.6. Разбиение криволинейного сектора
|
Теорема 2. Площадь криволинейного сектора вычисляется по формуле:
 .
.
► Для вычисления площади криволинейного сектора ОАВ применяется алгоритм составления интегральной суммы с последующим предельным переходом к определенному интегралу.
1. Разобьем отрезок  на
на 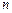 частичных отрезков точками
частичных отрезков точками 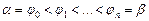 . Обозначим
. Обозначим  ,
,  . Проведем лучи
. Проведем лучи 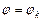 ,
,  . Тогда криволинейный сектор ОАВ разобьется на
. Тогда криволинейный сектор ОАВ разобьется на 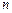 частичных криволинейных секторов (рис.6).
частичных криволинейных секторов (рис.6).
|
|
|
2. На каждом частичном отрезке  ,
,  , выберем произвольным образом точку
, выберем произвольным образом точку  и найдем значения функции
и найдем значения функции  в этих точках:
в этих точках:  ,
,  .
.
3. Предположим, что на каждом из частичных отрезков  функция
функция 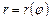 постоянна и совпадает со значением
постоянна и совпадает со значением  . Тогда каждый частичный криволинейный сектор можно заменить круговым сектором с радиусом
. Тогда каждый частичный криволинейный сектор можно заменить круговым сектором с радиусом  и центральным углом
и центральным углом  . Площадь такого кругового сектора вычисляется по формуле
. Площадь такого кругового сектора вычисляется по формуле
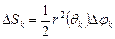 .
.
За площадь  криволинейного сектора ОАВ примем площадь фигуры, состоящей из
криволинейного сектора ОАВ примем площадь фигуры, состоящей из 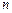 частичных круговых секторов:
частичных круговых секторов:
 .
.
Приближенное равенство тем точнее, чем меньше отрезки  , т.е. чем больше
, т.е. чем больше 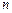 . Правая часть равенства является интегральной суммой для непрерывной функции
. Правая часть равенства является интегральной суммой для непрерывной функции  на отрезке
на отрезке  .
.
4. За точное значение площади  криволинейного сектора ОАВ принимается предел интегральной суммы при
криволинейного сектора ОАВ принимается предел интегральной суммы при  :
:
 . ◄
. ◄
Пример. Вычислить площадь криволинейного сектора, ограниченного кардиоидой
 ,
,
где  .
.
Решение. Имеем
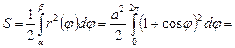
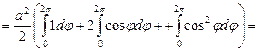
 .
.
Длина дуги кривой.
Длина дуги плоской кривой в декартовой системе координат.Пусть функция 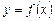 определена и непрерывна на отрезке
определена и непрерывна на отрезке  и кривая
и кривая  – график этой функции (рис.8). Требуется найти длину дуги плоской кривой
– график этой функции (рис.8). Требуется найти длину дуги плоской кривой  , заключенной между вертикальными прямыми
, заключенной между вертикальными прямыми  и
и  .
.
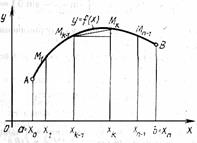
Рис.7. Разбиение дуги на частичные дуги
Разобьем отрезок  произвольным образом на
произвольным образом на 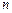 частей точками (рис.7)
частей точками (рис.7)
 .
.
Обозначим 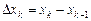 ,
,  . Через точки
. Через точки  ,
,  , проведем вертикальные прямые, параллельные оси Оу, до пересечения с кривой
, проведем вертикальные прямые, параллельные оси Оу, до пересечения с кривой  . Тогда дуга
. Тогда дуга 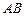 разобьется на
разобьется на 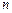 частей. Соединив каждые две соседние точки разбиения кривой
частей. Соединив каждые две соседние точки разбиения кривой  отрезками (хордами), получим ломаную
отрезками (хордами), получим ломаную  , вписанную в дугу
, вписанную в дугу 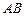 . Обозначим длину ломаной через
. Обозначим длину ломаной через 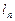 :
:
 ,
,
где  – длина хорды, стягивающей дугу
– длина хорды, стягивающей дугу  .
.
Длина ломаной является приближенным значением длины дуги 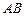
 . Очевидно, что если увеличивать число
. Очевидно, что если увеличивать число 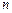 точек разбиения отрезка
точек разбиения отрезка  на частичные отрезки так, чтобы длина максимального из них стремилась к нулю, то длина вписанной ломаной стремится к длине дуги кривой
на частичные отрезки так, чтобы длина максимального из них стремилась к нулю, то длина вписанной ломаной стремится к длине дуги кривой 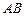
Если существует конечный предел 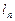 при
при  , то этот предел называется длиной дуги
, то этот предел называется длиной дуги  , а сама дуга называется спрямляемой:
, а сама дуга называется спрямляемой:
 .
.
Если конечный предел 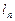 не существует, то и длина дуги не существует, а сама дуга называется неспрямляемой.
не существует, то и длина дуги не существует, а сама дуга называется неспрямляемой.
|
|
|
Теорема 3. Если функция  . на отрезке
. на отрезке  имеет непрерывную производную
имеет непрерывную производную  , то кривая
, то кривая  – спрямляемая, и ее длина вычисляется по формуле
– спрямляемая, и ее длина вычисляется по формуле
 .
.
►Вычислим длину стягивающей хорды  . Так как
. Так как  ,
,  , то
, то
 .
.
По теореме Лагранжа имеем
 ,
,  .
.
Следовательно,  .
.
Подставляя полученное выражение, получаем
 .
.
В правой части формулы стоит интегральная сумма для функции:  на отрезке
на отрезке  . Предел такой суммы существует и равен определенному интегралу от этой функции на отрезке
. Предел такой суммы существует и равен определенному интегралу от этой функции на отрезке  :
:
 . ◄
. ◄
Пример. Вычислить длину дуги полукубической параболы  , если
, если  .
.
Решение. Имеем
 .
.
В параметрическом виде. Пусть уравнение кривой задано параметрическими уравнениями
 ,
,
 ,
,
где  ,
,  ,
,  – непрерывные функции с непрерывными производными, причем
– непрерывные функции с непрерывными производными, причем 
 .
.
Для вычисления длины дуги кривой воспользуемся формулой  , предварительно выполнив замену переменной:
, предварительно выполнив замену переменной:  . Тогда
. Тогда  и
и  .
.
Подставляя в формулу дины дуги, получим:
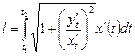
или  .
.
Если пространственная кривая задана параметрическими уравнениями  ,
,  ,
, 
 , где
, где  ,
,  ,
,  – непрерывные функции, имеющие непрерывные производные на отрезке
– непрерывные функции, имеющие непрерывные производные на отрезке  , то длина дуги этой кривой определяется по формуле
, то длина дуги этой кривой определяется по формуле
 .
.
Пример. Вычислить длину астроиды
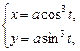
если  .
.
Решение. В силу симметричности астроиды относительно осей ее длина  равна
равна
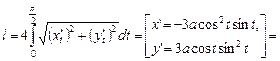
 .
.
В полярной системе координат.Пусть кривая задана в полярной системе координат уравнением 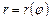
 . Предположим, что
. Предположим, что  и
и  непрерывны на отрезке
непрерывны на отрезке  .
.
Декартовы и полярные координаты связаны соотношениями:
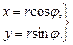
Учитывая, что 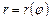 , получаем
, получаем
 ,
,  .
.
Эти уравнения можно рассматривать как параметрические уравнения кривой.
Найдем производные от  и
и  по параметру
по параметру  :
:
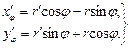
Отсюда 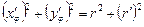
Следовательно,  .
.
Пример. Вычислить длину первого витка спирали Архимеда  .
.
Решение. Первый виток спирали образуется при изменении полярного угла  . Поэтому
. Поэтому
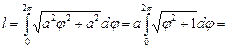
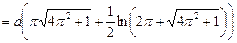 .
.
|
|
|


