Термодинамика идеальных растворов.

Глава 4

Введение.

Приближение идеального газа можно применить к модели идеального раствора и использовать соответствующие термодинамические равенства. В случае идеальных растворов, в отличие от идеальных газов, нельзя пренебречь потенциальной энергией взаимодействия между молекулами по сравнению с кинетической энергией их теплового движения.

Приближение идеальности в данном случае означает пренебрежимо малое различие в межмолекулярных взаимодействиях между однородными и разнородными молекулами в жидком растворе. Для этого разнородные молекулы должны иметь примерно одинаковые размеры и близкое химическое строение. Такими свойствами обладают жидкие растворы бензола и толуола, метилового и этилового спирта, твёрдые растворы изотопов различных веществ.

Фазовые равновесия. Двухкомпонентные, трёхкомпонентные системы.

Сначала рассмотрим жидкие идеальные растворы, посмотрим, какими термодинамическими величинами они характеризуются. Потом рассмотрим явления, связанные с выделением твёрдых фаз, твёрдые растворы.

Бинарные системы. Трёхмерная диаграмма T, P, X. Двухкомпонентный идеальный жидкий раствор.

Фазовые превращения в бинарной системе могут быть представлены трёхмерной диаграммой с координатами T, P, X (мольная доля). Простой случай рассмотрим на примере бинарной системы, где существует только пар и единственная жидкая фаза (не рассматриваем область равновесия между твёрдой и жидкой фазами).

DB - график зависимости P_пара от Тдля толуола.

АС - график зависимости P_пара от Тдля бензола.

Две поверхности внутри параллелепипеда:

верхняя (l) - общее давление пара как f(T, мольной доли толуола в жидкости0)

нижняя (v) - изобарный состав пара, равновесного с жидкостью, его состав.

Выше поверхности l - жидкость (жидкая фаза).

Ниже поверхности v - пар.

Область между поверхностями - сосуществование пара и жидкой фазы.

Если существуют 4 фазы, то система инвариантна.

Упростим:

Рассмотрим сечение полной трёхмерной диаграммы плоскостями. На рисунке давление пара бензола и толуола над их бинарными растворами при T = const.

Общее давление равно сумме парциальных давлений.

Пусть T=const (60⁰), (т.е. передняя грань), получим кривую l - общее давление пара l=p₁+p₂ в зависимости от состава жидкости. Оно складывается из парциальных давлений бензола и толуола.

"PX" диаграмма:

Кривая v - получается, если по вертикали по-прежнему откладывать общее давление, а по горизонтали - состав пара. Кривая пара (v) даёт те давления, при которых пар данного состава начинает конденсироваться, когда увеличивается P. Выше l - область жидкости. Ниже v - область пара. Между ними - область из жидкости и пара.

Соотношение Рауля (закон Рауля 1884 год, для идеальных растворов).

Из рисунка видно: давление пара бензола над смесями бензола и толуола пропорционально мольной доле бензола в растворе, коэффициент пропорциональности равен довлению пара чистого бензола (тоже для толуола).

Пусть 1, 2 - компоненты бинарного раствора.

p₁=x₁p₁⁰

p₂=x₂p₂⁰

(4.1)

p₁⁰ - давление пара чистых компонентов при Т раствора.

Общее давление = 1атм. При наличии воздуха существенных изменений не наблюдается. Растворы, подчиняющиеся закону Рауля, называются идеальными.

Мольная доля компонента в паре равна доле, которую составляет его давление от общего давления пара, её можно рассчитать:

(4.2)

Далее увидим, даже в случае неидеальных растворов, закон Рауля применим к компоненту, мольная доля которого в растворе

Термодинамика идеальных растворов.

Ищем химический потенциал компонента в растворе. Знаем, что при равновесии химический потенциал компонента i имеет одно и то же значение в жидкой фазе и в паре.

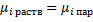
(1)

Из условия химического равновесия (следующая глава) для смеси идеальных газов химический потенциал компонента i в газовой смеси выражается

(4.3)

- парциальное уравнение компонента i

- µ компонента i при =1атм.

Пусть раствор идеальный => подчиняется закону Рауля и химический потенциал компонента i в паре можно выразить через его мольную долю 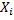в растворе.

Вернёмся к (1) соотношению

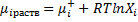
(4.4)

Отсюда, если 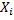=1 - чистое вещество, то - химический потенциал чистого жидкого компонента.

(4.4) - это есть определение идеальных растворов.

Термодинамические соотношения для идеальных жидких растворов и газовых смесей (при меняется и для идеальных твёрдых растворов) близки.

Для вычисления изобарного потенциала G двух жидкостей до и после их смешения с образованием идеального раствора можно воспользоваться

есть сумма вкладов всех компонентов.

Т.е. изобарный потенциал n₁ молей жидкости 1 и n₂ молей жидкости 2 до смешения равен:

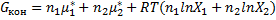
G смешения:

(4.5)

где n=n₁+n₂.

Отметим, что это уравнение тождественно уравнению для процесса смешения идеальных газов и их графики совпадают.

Двухкомпонентные системы, состоящие из твёрдых и жидких фаз. Рассмотрим смесь двух газов или двух жидкостей, будем считать, что они идеальны (все выводы совпадают).

Поскольку мольные доли меньше 1, члены содержащие ln<0 и <0. Это соответствует тому, что смешение газов (жидкостей) при постоянных T и P является самопроизвольным процессом.

На рисунке смешения представлен как функция мольной доли одного из жидкостей (газов). Наименьшее значение смешения имеет при x₁=x₂=1/2.

Согласно (2.21) энтропию смешения двух жидкостей с образованием идеального раствора

(4.6)

Поскольку

Таким образом, идеальные газы (жидкости) смешиваются при постоянных T и P без теплового эффекта.

Это соответствует тому, что между молекулами идеальных газов (жидкостей) нет ни притяжения, ни отталкивания. Следовательно, если рассматривать энергию системы, то нет разницы между случаями, когда газы (жидкости) смешаны и когда они изолированы друг от друга.

"Движущая сила", приводящая к смещению, связана исключительно с изменениями энтропии. С точки зрения статистической физики, равновесию отвечает именно смесь, т.к. вероятность этого состояния больше. (Об этом мы говорили, когда рассматривали диффузию в кристаллах).

Знаем, что

(2.21)

при смешении идеальных газов.

Или, (что тоже самое), при смешении компонентов с образованием идеального раствора объём не меняется.

Отметим, что выведенные термодинамические соотношения применяются и для идеальных твёрдых растворов.

С другой стороны, возможны случаи, когда компоненты не смешиваются в жидком состоянии или смешиваются в жидком состоянии и не смешиваются в твёрдом состоянии. (Пример: Bi-Cd).

Тогда потенциал Гиббса смешения как функция мольной доли одного из компонентов будет выглядеть так:

Зависимость мольного потенциала Гиббса от состава системы в случае полной несмешиваемости компонентов.

Говорят, что образуется смесь двух фаз (или механическая смесь).

 

4.3 Диаграмма TX (состав-Т_кип) для бинарных растворов.

До сих пор рассматривали диаграммы - сечения 3 мерной диаграммы плоскостью T const, в частности Pпара(Х).

Рассмотрим сечение P const (верхняя грань параллелепипеда) Tкип(Х).

Раствор закипает когда

Сумма парциальных давлений (общее давление) = давлению внешнему.

Кривая пара всегда лежит выше кривой жидкости на графиках зависимости T_кип(Х).

Лежит ниже - на графиках Pпара(Х). Жидкость кипит при температурах, изображаемых нижней кривой.

 

Для практики имеет большое значение случай, когда растворённое вещество имеет пренебрежимо малое давление пара и P_пара 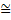P_{пара растворителя}. Для идеальных растворов давление пара растворителя определяется законами Рауля.

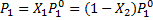
1 - растворитель.

2 - нелетучее растворённое вещество.

Для неидеальных растворов это уравнение можно использовать, когда мольная доля растворённого вещества X₂<<X₁, следовательно можно пренебречь влиянием растворённого вещества на растворитель. Тогда:

В результате понижения P пара над раствором нелетучего вещества повышается температура кипения раствора, что позволяет вычислить молекулярный вес растворённого вещества. Для воды повышение ΔТ_кип в идеальном одномоляльном растворе нелетучего вещества 0,513K.

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: