 |
Интерференция волн. Стоячие волны. Уравнение стоячей волны
|
|
|
|
Глава 7. Механические волны
Волны. Уравнение волны
Помимо уже рассмотренных нами движений, почти во всех областях физики встречается ещё один тип движения – волны. Отличительной особенностью этого движения, делающей его уникальным, является то, что в волне распространяются не сами частицы вещества, а изменения в их состоянии (возмущения).
Возмущения, распространяющиеся в пространстве с течением времени, называются волнами. Волны бывают механические и электромагнитные.
Упругие волны – это распространяющиеся возмущения упругой среды.
 Возмущение упругой среды – это любое отклонение частиц этой среды от положения равновесия. Возмущения возникают в результате деформации среды в каком-либо её месте.
Возмущение упругой среды – это любое отклонение частиц этой среды от положения равновесия. Возмущения возникают в результате деформации среды в каком-либо её месте.
Совокупность всех точек, куда дошла волна в данный момент времени, образует поверхность, называемую фронтом волны.
По форме фронта волны делятся на сферические и плоские. Направление распространения фронта волны определяется перпендикуляром к фронту волны, называемым лучом. Для сферической волны лучи представляют собой радиально расходящийся пучок. Для плоской волны лучи- пучок параллельных прямых.
В любой механической волне одновременно существуют два вида движения: колебания частиц среды и распространения возмущения.
Волна, в которой колебания частиц среды и распространение возмущения происходят в одном направлении, называется продольной (рис.7.2 а).
Волна, в которой частицы среды колеблются перпендикулярно направлению распространения возмущений, называется поперечной (рис. 7.2 б).

В продольной волне возмущения представляют собой сжатие (или разрежение) среды, а в поперечной - смещения (сдвига) одних слоев среды относительно других. Продольные волны могут распространяться во всех средах (и в жидких, и в твёрдых, и в газообразных), а поперечные - только в твёрдых.
|
|
|
Каждая волна распространяется с некоторой скоростью. Под скоростью волны υ понимают скорость распространения возмущения. Скорость волны определяется свойствами среды, в которой эта волна распространяется. В твёрдых телах скорость продольных волн больше скорости поперечных.
Длиной волны λ называется расстояние, на которое распространяется волна за время, равное периоду колебания в её источнике. Поскольку скорость волны – величина постоянная (для данной среды), то пройденной волной расстояние равно произведению скорости на время её распространения. Таким образом, длина волны
λ= υТ (7. 1)
Из уравнения (7.1) следует, что частицы, отделённые друг от друга интервалом λ, колеблются в одинаковой фазе. Тогда можно дать следующее определение длины волны: длина волны есть расстояние между двумя ближайшими точками, колеблющимися в одинаковой фазе.
Выведем уравнение плоской волны, позволяющее определить смещение любой точки волны в любой момент времени. Пусть волна распространяется вдоль луча от источника с некоторой скоростью υ.
Источник возбуждает простые гармонические колебания, и смещение любой точки волны в любой момент времени определяетcz уравнением
S = Asinωt (7. 2)
Тогда точка среды, отстоящая от источника волны на расстоянии х, также будет совершать гармонические колебания, но с запаздыванием по времени на величину 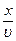 , т.е. на время, необходимое для распространения колебаний от источника до этой точки. Смещение колеблющейся точки относительно положения равновесия в любой момент времени будет описываться соотношением
, т.е. на время, необходимое для распространения колебаний от источника до этой точки. Смещение колеблющейся точки относительно положения равновесия в любой момент времени будет описываться соотношением
 (7. 3)
(7. 3)
Это и есть уравнение плоской волны. Эта волна, характеризуется следующими параметрами:
· S — смещение от положения равновесии точки упругой среды, до которой дошло колебание;
|
|
|
· ω — циклическая частота колебаний, генерируемых источником, с которой колеблются и точки среды;
· υ — скорость распространения волны (фазовая скорость);
· х – расстояние до той точки среды, куда дошло колебание и смещение которой равно S;
· t – время отсчитываемое от начала колебаний;
Вводя в выражение (7. 3) длину волны λ, уравнение плоской волны можно записать так:
 (7. 4)
(7. 4)
 или
или
 (7. 5)
(7. 5)
где 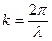 называется волновым числом (число волн, приходящихся на единицу длины).
называется волновым числом (число волн, приходящихся на единицу длины).
Волновое уравнение
Уравнение плоской волны (7. 5) - одно из возможных решений общего дифференциального уравнения с частными производными, описывающего процесс распространения возмущения в среде. Такое уравнение называется волновым. В уравнения (7.5) входят переменные t и х, т.е. смещение периодически меняется и во времени и в пространстве S = f(x, t). Волновое уравнение можно получить, если продифференцировать (7. 5) дважды по t:
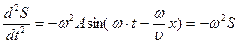
И дважды по х

Подставляя первое уравнение во второе, получаем уравнение плоской бегущей волны вдоль оси X:
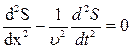 (7. 6)
(7. 6)
Уравнение (7.6) называют волновым, и для общего случая, когда смещение является функцией четырех переменных, оно имеет вид
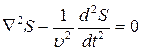 (7.7)
(7.7)
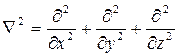 , где
, где  —оператор Лапласа
—оператор Лапласа
§ 7.3 Энергия волны. Вектора Умова.
При распространении в среде плоской волны
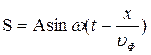 (7.8)
(7.8)
происходит перенос энергии. Мысленно выделим элементарный объем ∆V, настолько малый, что скорость движения и деформацию во всех его точках можно считать одинаковыми и равными соответственно
 и
и  (7.9)
(7.9)
Выделенный объём обладает кинетической энергией
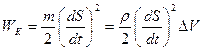 (7.10)
(7.10)
m=ρ∆V — масса вещества в объеме ∆V, ρ — плотность среды].
 (7.11)
(7.11)
Подставляя в (7.10) значение  , получаем
, получаем
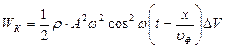 (7.12)
(7.12)
Максимумы кинетической энергии приходятся на те точки среды, которые проходят положения равновесия в данный момент времени (S = 0), в эти моменты времени колебательное движение точек среды характеризуется наибольшей скоростью.
Рассматриваемый объем ∆V обладает также потенциальной энергией упругой деформации 
[Е — модуль Юнга; 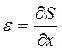 — относительное удлинение или сжатие].
— относительное удлинение или сжатие].
Учитывая формулу (7.8) и выражение для производной, находим, что потенциальная энергия равна
|
|
|
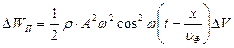 (7.13)
(7.13)
Анализ выражений (7.12) и (7.13) показывает, что максимумы потенциальной и кинетической энергий совпадают. Следует отметить, что это является характерной особенностью бегущих волн. Чтобы определить полную энергию объема ∆V, нужно взять сумму потенциальной и кинетической энергий:
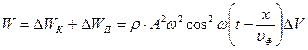 (7.14)
(7.14)
Разделив эту энергию на объем, в котором она содержится, получим плотность энергии:
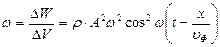 (7.15)
(7.15)
Из выражения (7.15) следует, что плотность энергии является функцией координаты х, т. е. в различных точках пространства она имеет различные значения. Максимального значения плотность энергии достигает в тех точках пространства, где смещение равно нулю (S = 0). Средняя плотность энергии в каждой точке среды равна
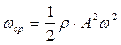 (7.16)
(7.16)
так как среднее значение 
Таким образом, среда, в которой распространяется волна, обладает дополнительным запасом энергии, которая доставляется от источника колебаний в различные области среды.
Перенос энергии в волнах количественно характеризуется вектором плотности потока энергии. Этот вектор для упругих волн называют вектором Умова (по имени русского ученого Н. А. Умова). Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени сквозь единичную площадку, расположенную перпендикулярно направлению распространения волны.
Интерференция волн. Стоячие волны. Уравнение стоячей волны
 Стоячие волны образуются в результате интерференции двух встречных плоских волн одинаковой частоты ω и амплитуды А.
Стоячие волны образуются в результате интерференции двух встречных плоских волн одинаковой частоты ω и амплитуды А.
Представим себе, что в точке S (рис.7.4) находится вибратор, от которого вдоль луча SO распространяется плоская волна. Достигнув преграды в точке О, волна отразится и пойдёт в обратном направлении, т.е. вдоль луча распространяются две бегущие плоские волны: прямая и обратная. Эти две волны когерентны, так как рождены одним и тем же источником и, накладываясь друг на друга, будут интерферировать между собой.
Возникающее в результате интерференции колебательное состояние среды и называется стоячей волной.
|
|
|
Запишем уравнение прямой и обратной бегущей волны:
прямая - 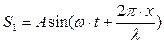 ; обратная -
; обратная - 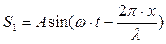
где S1 и S2 – смещение произвольной точки на луче SO. С учётом формулы для синуса суммы результирующее смещение равно
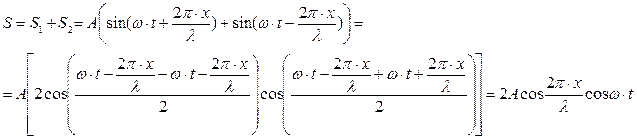
Таким образом, уравнение стоячей волны имеет вид
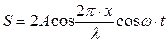 (7.17)
(7.17)
Множитель cosωt показывает, что все точки среды на луче SО совершают простые гармонические колебания с частотой 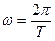 . Выражение
. Выражение 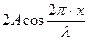 называется амплитудой стоячей волны. Как видно, амплитуда определяется положением точки на луче SO (х).
называется амплитудой стоячей волны. Как видно, амплитуда определяется положением точки на луче SO (х).
Максимальное значение амплитуды будут иметь точки, для которых
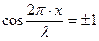 или
или 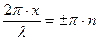 (n = 0, 1, 2,….)
(n = 0, 1, 2,….)
откуда  , или
, или 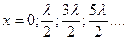 (7.18)
(7.18)
Точки, имеющие такие координаты, называют пучностями стоячей волны.
Минимальное значение, равное нулю, будут иметь те точки для которых
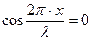 или
или 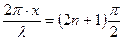 (n = 0, 1, 2,….)
(n = 0, 1, 2,….)
откуда 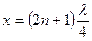 или
или 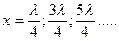 (7.19)
(7.19)
Точки, имеющие такие координаты, называют узлами стоячей волны. Сопоставляя выражения (7.18) и (7.19), видим, что расстояние между соседними пучностями и соседними узлами равно λ/2.
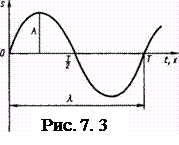
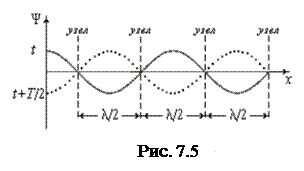 На рисунке сплошной линией изображено смещение колеблющихся точек среды в некоторый момент времени, пунктирной кривой – положение этих же точек через Т/2. Каждая точка совершает колебания с амплитудой, определяемой её расстоянием от вибратора (х).
На рисунке сплошной линией изображено смещение колеблющихся точек среды в некоторый момент времени, пунктирной кривой – положение этих же точек через Т/2. Каждая точка совершает колебания с амплитудой, определяемой её расстоянием от вибратора (х).
В отличие от бегущей волны в стоячей волне не происходит переноса энергии. Энергия просто переходит из потенциальной (при максимальном смещении точек среды от положения равновесия) в кинетическую (при прохождении точками положения равновесия)в пределах между узлами, остающимися неподвижными.
 Все точки стоячей волны в пределах между узлами колеблются в одинаковой фазе, а по разные стороны от узла – в противофазе.
Все точки стоячей волны в пределах между узлами колеблются в одинаковой фазе, а по разные стороны от узла – в противофазе.
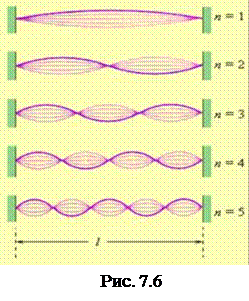
Стоячие волны возникают, например, в закреплённой с обоих концов натянутой струне при возбуждении в ней поперечных колебаний. Причём в местах закреплений располагаются узлы стоячей волны.
Если стоячая волна устанавливается в воздушном столбе, открытом с одного конца (звуковая волна), то на открытом конце образуется пучность, а на противоположном – узел.
Примеры решения задач
Пример. Определите скорость распространения звука в воде, если длина волны равна 2м, а частота колебаний источника ν=725Гц. Определите также наименьшее расстояние между точками среды, колеблющимися в одинаковой фазе.
Дано: λ=2м; ν=725Гц.
Найти: υ; х.
Решение. Длина волны равна расстоянию, на которое распространяется определённая фаза волны за период Т, т.е.
 ,
,
где υ – скорость волны; ν - частота колебаний.
Тогда искомая скорость
υ=λν.
Длина волны – расстояние между ближайшими частицами среды, колеблющимися в одинаковой фазе. Следовательно, искомое наименьшее расстояние между точками среды, колеблющимися в одинаковой фазы, равно длине волны, т.е.
|
|
|
х=λ
Ответ: υ=1450 м/с; х=2м.
Пример. Определите, во сколько раз изменится длина ультразвуковой волны при переходе её из меди в сталь, если скорость распространения ультразвука в меди и стали соответственно равны υ1=3,6км/с и υ2=5,5 км/с.
Дано: υ1=3,6км/с=3,6∙103м/с. и υ2=5,5 км/с =5,5∙103м/с.
Найти: 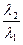 .
.
Решение. При распространении волн частота колебаний не изменяется при переходе их одной среды в другую (она зависит только от свойств источника волн), т.е. ν1= ν2= ν.
Связь длины волны с частотой ν:
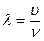 , (1)
, (1)
где υ – скорость волны.
Искомое отношение, согласно (1),
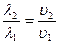 .
.
Вычисляя, получаем 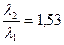 (увеличится в 1.53 раза).
(увеличится в 1.53 раза).
Ответ: 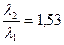
Пример. Один конец упругого стержня соединён с источником гармонических колебаний, подчиняющихся закону  , а другой конец жёстко закреплён. Учитывая, то отражение в месте закрепления стержня происходит от более плотной среды, определите: 1) уравнение стоячей волны; 2) координаты узлов; 3) координаты пучностей.
, а другой конец жёстко закреплён. Учитывая, то отражение в месте закрепления стержня происходит от более плотной среды, определите: 1) уравнение стоячей волны; 2) координаты узлов; 3) координаты пучностей.
Дано:  .
.
Найти: 1) ξ (x, t); 2) ху; 3) хn.
Решение. Уравнение падающей волны
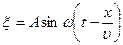 , (1)
, (1)
где А – амплитуда волны; ω - циклическая частота; υ - скорость волны.
Согласно условию задачи, отражение в месте закрепления стержня происходит от более плотной среды, поэтому волна меняет фазу на противоположную, и уравнение отражённой волны
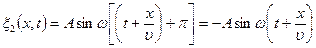 . (2)
. (2)
Сложив уравнения (1) и (2), получим уравнение стоячей волны
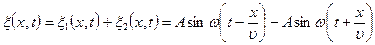
откуда

(учли 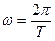 ; λ=υТ).
; λ=υТ).
В точках среды, где
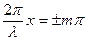 (m=0, 1, 2,….) (3)
(m=0, 1, 2,….) (3)
Амплитуда колебаний обращается в нуль (наблюдаются узлы), в точках среды, где
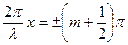 (m=0, 1, 2,….) (4)
(m=0, 1, 2,….) (4)
Амплитуда колебаний достигает максимального значения, равного 2А (наблюдаются пучности). Искомые координаты узлов и пучностей находим из выражений (3) и (4):
координаты узлов 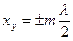 (m=0, 1, 2,….);
(m=0, 1, 2,….);
координаты пучностей  (m=0, 1, 2,….).
(m=0, 1, 2,….).
Ответ: 1) 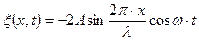 ;
; 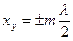 (m=0, 1, 2,….);
(m=0, 1, 2,….);  (m=0, 1, 2,….).
(m=0, 1, 2,….).
Пример. Расстояние между соседними узлами стоячей волны, создаваемый камертоном в воздухе ℓ =42см. Принимая скорость звука в воздухе υ=332 м/с, определите частоту колебаний ν камертона.
Дано: ℓ =42см=0,42м; υ=332 м/с.
Найти: ν.
Решение. В стоячеё волне расстояние между двумя соседними узлами равно 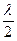 . Следовательно, ℓ=
. Следовательно, ℓ= 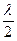 , откуда длина бегущей волны
, откуда длина бегущей волны
λ=2ℓ (1)
Связь между длиной волны и частотой  . Подставив в эту формулу значение (1), получим искомую частоту колебаний камертона
. Подставив в эту формулу значение (1), получим искомую частоту колебаний камертона
 .
.
Ответ: ν=395 Гц.
Пример. Труба длиной ℓ = 50см заполнена воздухом и открыта с одного конца. Принимая скорость υ звука равной 340 м/с, определите, при какой наименьшей частоте в трубе будет возникать стоячая звуковая волна. Принимая скорость звука в воздухе υ=332 м/с, определите частоту колебаний ν камертона.
Дано: ℓ =50см=0,5м; υ=340 м/с.
Найти: ν0.
Решение. Частота будет минимальной при условии, что длина стоячей волны максимальна.
В открытой с одного конца трубе на открытой части будет пучность (отражение от менее плотной среды), а на закрытой части – узел (отражение от более плотной среды). Поэтому в трубе уложится четверть длины волны:

Учитывая, что длина волны  , можем записать
, можем записать
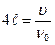 ,
,
Откуда искомая наименьшая частота
 .
.
Ответ: ν0=170 Гц.
Пример. Два электропоезда движутся навстречу друг другу со скоростями υ1=20 м/с и υ2=10 м/с. Первый поезд даёт свисток, высота тона которого соответствует частоте ν0=600 Гц. Определите частоту, воспринимаемую пассажиром второго перед встречей поездов и после их встречи. Скорость звука принять равной υ=332 м/с.
Дано: υ1=20 м/с; υ2=10 м/с; ν0=600 Гц; υ=332 м/с.
Найти: ν; ν'.
Решение. Согласно общей формуле, описывающей эффект Доплера в акустике, частота звука, воспринимаемая движущимся приёмником,
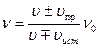 , (1)
, (1)
где ν0- частота звука, посылаемая источником; υпр - скорость движения приёмника; υист - скорость движения источника. Если источник и приёмник приближаются друг к другу, то берётся верхний знак, если удаляются – нижний знак.
Согласно обозначениями, данным в задаче (υпр=υ2 и υист=υ1) и приведённым выше пояснениями, из формулы (1) искомые частоты, воспринимаемые пассажиром второго поезда:
Перед встречей поездов (электропоезда сближаются):
 ;
;
После встречи поездов (поезда удаляются друг от друга):
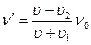
Ответ: ν=658 Гц; ν' =549 Гц.
|
|
|


