 |
Математические модели описания статистических характеристик ошибок в
|
|
|
|
ЛЕКЦИЯ 6
Математические модели описания статистических характеристик ошибок в
программах.
План.
1. Контрольный опрос
2. Предназначение математических моделей;
3. Первая группа допущений;
4. Вторая группа допущений;
5. Третья группа допущений.
Детальный анализ проявления ошибок показывает их глубокую связь с методами структурного построения программ, типом языка программирования, степенью автоматизации технологии проектирования и многими другими факторами. Статистические характеристики различных типов ошибок трудно описать математическими моделями, и более доступны для математического описания обобщенные характеристики ошибок в комплексе программ. Путем анализа и обобщения экспериментальных данных реальных разработок предложено несколько математических моделей, описывающих основные закономерности изменения суммарного количества вторичных ошибок в программах. Модели имеют вероятностный характер, и достоверность прогнозов в значительной степени зависит от точности исходных данных и глубины прогнозирования по времени. Эти математические модели предназначены для оценки:
1. надежности функционирования комплекса программ в процессе отладки, испытаний и эксплуатации;
2. числа ошибок, оставшихся невыявленными в анализируемых программах;
3. времени, требующегося для обнаружения следующей ошибки в функционирующей программе;
4. времени, необходимого для выявления всех ошибок с заданной вероятностью.
Точное определение полного числа невыявленных ошибок в комплексе программ прямыми методами измерения невозможно. Однако имеются пути для приближенной статистической оценки их полного числа или вероятности ошибки в каждой команде программы. Такие оценки базируются на построении математических Моделей в предположении о жесткой корреляции между общим количеством и
|
|
|
проявлениями ошибок в комплексе программ после его отладки в течение времени T, т. е. между:
· суммарным количеством первичных ошибок в комплексе программ (n0) или вероятностью ошибки в каждой команде программы (p0);
· количеством ошибок, выявляемых в единицу времени в процессе тестирования и отладки при постоянных усилиях на ее проведение {dn/dt);
· интенсивностью искажений результатов в единицу времени (l) на выходе комплекса программ вследствие невыявленных первичных ошибок при функционировании программ.
Наиболее доступно для измерения количество вторичных ошибок в программе, выявляемых в единицу времени в процессе отладки. Возможна также непосредственная регистрация отказов и наиболее крупных искажений результатов, выявляемых средствами оперативного контроля в процессе функционирования программ. Все три показателя связаны некоторыми коэффициентами пропорциональности, значения которых зависят, в частности, от интервала времени, на котором производится сопоставление, от быстродействия ЭВМ, от эффективности средств автоматизации отладки и от некоторых других параметров. При фиксированных условиях разработки и функционирования конкретного комплекса программ эти коэффициенты имеют вполне определенное значения. Для другой подобной системы коэффициенты могут несколько измениться, однако оценки, полученные для нескольких конкретных систем, позволяют прогнозировать эти характеристики, а следовательно, и соответствующие показатели надежности ПС в зависимости от длительности отладки и ряда других факторов.
Описаны несколько математических моделей, основой которых являются различные гипотезы о характере проявления вторичных ошибок в программах. Эти гипотезы в той или иной степени апробированы при обработке данных реальных разработок, и их можно разделить на три группы. В первую группу входят очевидные допущения, статистическая проверка которых невозможна и нецелесообразна. Вторую группу составляют допущения, определяющие специфические характеристики модели и требующие статистической проверки и обоснования на базе экспериментальных исследований. В третью группу включены второстепенные допущения, расширяющие и уточняющие возможности применения модели и частично доступные экспериментальной проверке.
|
|
|
Первая группа допущений включает предположение о наблюдаемости искажений данных, программ или вычислительного процесса, обусловленных первичными ошибками в программах. Первичная ошибка, являющаяся причиной искажения результатов, либо фиксируется и исправляется после завершения этапа тестирования, либо вообще не обнаруживается, так как проявление ее последствий незначительно.
Предполагается, что множество тестов более или менее равномерно покрывает все множество реальных исходных данных и отсутствуют априорные сведения для искусственного повышения интенсивности ошибок при некоторых тестах. Тем самым состав тестов представляется случайным относительно области изменения входных данных программы и содержащихся в ней необнаруженных первичных ошибок.
Наличие большого числа разнообразных данных, необходимых для исполнения программ, и практически некоррелированное их изменение приводит к внешне случайному выбору маршрута, по которому исполняется программа в каждом конкретном случае. В
результате интенсивность проявления ошибок при реальном функционировании программ зависит от среднего быстродействия ЭВМ и практически не зависит от конкретного распределения типов команд на маршрутах обработки данных между ошибками.
Коллектив специалистов, их квалификация и загруженность предполагаются постоянными на интервале проектирования и исследования характеристик ошибок. Также постоянным считается доступное машинное время для проведения проверок программ.
Вторая группа допущений при построении математических моделей ошибок является основной и проверена интегрально по обобщенным характеристикам частости обнаружения ошибок и дифференцирование путем анализа правомерности каждого допущения. Ниже рассмотрены допущения при построении экспоненциальной модели.
|
|
|
Интервалы времени между обнаруживаемыми искажениями результатов предполагаются статистически независимыми. Время измеряется по фактической наработке длительностей исполнения программ t без учета дополнительных затрат календарного времени на локализацию, диагностику и исправление ошибок.
Предполагается, что интенсивность проявления ошибок остается постоянной, пока не произведено исправление первичной ошибки или не изменена программа по другой причине. Если каждая обнаруженная ошибка исправляется, то значения интервалов времени между их проявлениями изменяются по экспоненциальному закону. Интегральная проверка распределения интервалов времени между обнаружениями ошибок показала, что оно достаточно хорошо аппроксимируется экспонентой.
Логично предположить, что интенсивность обнаружения ошибок пропорциональна суммарному числу первичных ошибок, имеющихся в данный момент в комплексе программ. Это допущение подтверждено расчетом значений суммарного числа ошибок для хорошо отлаженных и переданных в эксплуатацию комплекса программ на ряд предыдущих моментов времени, когда проводилась отладка.
Каждая обнаруженная ошибка подлежит исправлению, поэтому предполагается, что частота исправления ошибок пропорциональна частоте их обнаружения. Однако некоторые исправления, в свою очередь, содержат ошибки. Кроме того, некоторые ошибки являются связанными, и при обнаружении проявления одной ошибки следует исправление нескольких первичных ошибок. Из-за этого частота обнаружения ошибок и частота их исправления не равны, а должны быть связаны некоторым коэффициентом пропорциональности. Коэффициенты корреляции для исследованных комплексов программ довольно высокие — от 0, 52 до 0, 82 при среднем значении около 0, 68, т. е. достаточно хорошо подтверждают гипотезу.
|
|
|
Третья группа допущений детализирует использование ресурсов на корректировку программ и повышение их качества.
Приведенные предположения позволяют построить экспоненциальную математическую модель распределения моментов обнаружения ошибок в программах и установить связь между интенсивностью обнаружения ошибок при отладке dn/dt, интенсивностью проявления ошибок при нормальном функционировании программ l и числом первичных ошибок п. Предположим, что в начале отладки комплекса программ при t=0 в нем содержалось N0 первичных ошибок. После отладки в течение времени осталось п0 первичных ошибок и устранено п ошибок (n0 + n = N0). Время t соответствует длительности исполнения программы на ЭВМ для обнаружения ошибок и не учитывает время, необходимое для анализа результатов и проведения корректировок. Календарное время tк отладочных и испытательных работ с реальным комплексом программ значительно больше, так как после тестирования программ, на которое затрачивается машинное время т, необходимо время на анализ результатов, на обнаружение и локализацию ошибок, а также на их устранение.
При постоянных усилиях на отладку интенсивность обнаружения искажений вычислительного процесса, программ или данных вследствие еще не выявленных ошибок
пропорциональна количеству оставшихся первичных ошибок в комплексе программ. Предположение о сильной корреляции между значениями по и dn/dt проверено анализом реальных характеристик процесса обнаружения ошибок. Тогда
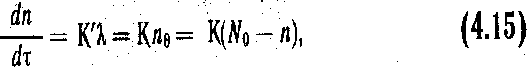(11. 1)_
где коэффициенты К и К' учитывают масштаб времени, используемый для
описания процесса обнаружения ошибок, быстродействие ЭВМ и другие параметры. Значение коэффициента К' можно определить как изменение темпа проявления искажений при переходе от функционирования программ на специальных тестах к функционированию на типовых исходных данных. В начале отладки это различие может быть значительным, однако при завершении отладки и при испытаниях тестовые данные практически совпадают с исходными данными при нормальной эксплуатации. Поэтому ниже К' полагается равным единице (К'=1).
Таким образом, интенсивность обнаружения ошибок в программе и абсолютное число устраненных первичных ошибок связываются уравнением
Так как выше предполагалось, что в начале отладки при t= 0 отсутствуют обнаруженные ошибки, то решение уравнения (11. 2) имеет вид
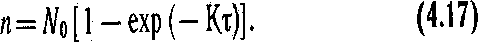
пропорционально интенсивности их обнаружения dn/d t с точностью до коэффициента К.
Наработка между проявлениями ошибок, которые, рассматриваются как
|
|
|
