 |
Алгоритм Краскала поиска остовного дерева минимальной длины
|
|
|
|
Основные понятия теории графов
Графом называется совокупность двух множеств, одним из которых является множество элементов, называемых вершинами, а другим - множество отношений между вершинами, называемых ребрами.
Пара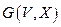 
называется простым графом, если 
– непустое конечное множество, элементы которого называются вершинами графа, а 
– конечное множество неупорядоченных пар различных элементов из V, называемых ребрами графа. Простой граф не содержит кратных ребер и петель.
Граф 
называется подграфом графа 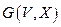, если 
, 
Граф получается стиранием некоторых ребер и вершин.
Объект, который содержит кратные ребра и петли, называется общим графом или мультиграфом.
Ографом или ориентированным графом 
называется пара множеств: V – конечное множество вершин и 
- множество упорядоченных пар элементов из V, т.е. граф, на рёбрах которого указывается направление.
Две вершины графа 
называются смежными, если существует ребро 
их соединяющее. При этом вершины u и v называются инцидентными этому ребру, а ребро называется инцидентным этим вершинам.
Два ребра называются смежными, если они имеют хотя бы одну общую вершину.
Вершина называется изолированной, если она не инцидентна ни одному ребру.
Вершина называется висячей, если она инцидентна только одному ребру.
Граф, имеющий ориентированные и неориентированные ребра, называется смешанным.
Степенью вершины v графа G называется число ребер 
, инцидентных данной вершине. Если - число чётное, то v – четная вершина. В противном случае 
– нечетная вершина. Петля учитывается 2 раза.
Лемма ( о рукопожатиях). Если m – общее число ребер графа 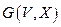, то
.
Два графа 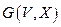и называются изоморфными, если:
|
|
|
1) существует биекция 
такая, что число ребер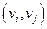 
, инцидентное вершинам 
графа G равно числу ребер 
, инцидентных вершинам 
графа 
, где 
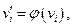
или
2) существуют две согласованные между собой биекции: 
(c учетом кратности ребер) такие, что: 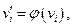а 
Теорема. Число нечетных вершин любого графа – четное.
Геометрической фигурой 
называется пара множеств 
где 
– некоторое множество точек в пространстве 
а Y – совокупность некоторых кривых линий, каждая из которых соединяет некоторые пары точек из множества В. Эти кривые соединяют пару точек 
, причем возможно вырождение этих кривых: 
Пусть эти кривые являются жордановыми, т.е. не имеют точек самопересечения, а друг с другом пересекаются только в точках множества В.
Геометрическая фигура в пространстве 
называется геометрической реализацией графа 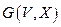, если они изоморфны, т.е. если существуют две биекции (согласованные между собой в указанном выше смысле): 
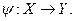
Если такая геометрическая фигура в пространстве существует, то говорят, что 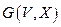может быть уложен в пространстве .
Конечным графом называется граф с конечным числом ребер.
Теорема. Каждый конечный граф может быть уложен в пространстве 
.
Плоским называется граф, изображенный на плоскости так, что никакие его 2 ребра не пересекаются геометрически нигде кроме инцидентной им вершины.
Граф, изоморфный плоскому графу, называется планарным.
Граф с n вершинами, у которого отсутствуют ребра, называется пустым или вполне несвязным графом.
Простой граф с n вершинами называется полным, если любые две его вершины являются смежными (соединены ребром).
Объединением двух графов 
и 
, где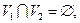 
называется граф G, который обозначается 
где 
Первое определение связного графа. Граф называется связным, если его нельзя представить в виде объединения двух графов и несвязным в противном случае. Всякий несвязный граф можно представить в виде объединения конечного числа связных графов, каждый из которых называется компонентом связности.
|
|
|
Маршруты, цепи, циклы
Маршрутом в графе 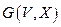называется конечная последовательность ребер вида: 
Этот маршрут обозначают: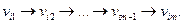 
Петля называется т ривиальным маршрутом.
Длиной маршрута называется число ребер в нем.
Маршрут называется цепью, если все его ребра различны.
Маршрут называется простой цепью, если все его вершины различны, за исключением, быть может, первой и последней.
Если 
то цепь называется замкнутой.
Замкнутая простая цепь, содержащая хотя бы одно ребро, называется циклом.
Две вершины 
называются эквивалентными или связанными, если существует простая цепь из одной вершины в другую.
Второе определение связного графа. Граф называется связным, если любые две его вершины являются связанными.
Теорема. Первое и второе определения связности равносильны.
Связанность вершин является отношением эквивалентности на множестве вершин графа.
Свойства отношения эквивалентности:
1) рефлексивность 
;
2) симметричность (если 
то 
);
3) транзитивность (если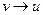 
и 
то 
)
Отношение эквивалентности задает разбиение графа на компоненты связности.
Теорема. Каждый граф единственным образом представляется в виде объединения непересекающихся связных подграфов (компонент связности).
Число реберв графе минимально, если удаление любого ребра приводит к увеличению компонент связности.
Если при удалении какого-то ребра в графе, число компонент связности увеличилось на единицу, то это ребро называется мостом или перешейком.
Числовые функции на графе
Говорят, что на вершинах графа 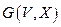реализуется числовая функция, если каждой вершине 
ставится в соответствие некоторое число 
из некоторого множества L.
Значением маршрута через вершины 
называется число 
.
Минимальным (максимальным) маршрутом через вершины некоторого множества маршрутов Р называется маршрут с минимальным (максимальным) значением λ.
Говорят, что на ребрах графа 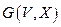реализуется числовая функция, если каждому ребру 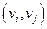сопоставлено число 
из некоторого множества М. Причем 
Значением маршрута через ребра, соединяющие вершины называется число 
Минимальным (максимальным) маршрутом через ребра некоторого множества маршрутов Р называется маршрут с минимальным (максимальным) значением λ.
|
|
|
Деревья и леса
Деревом называется связный неориентированный граф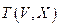 
или 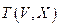без цикла.
Лесом называется неориентированный граф, компонентами связности которого являются деревья.
Теорема (характеристические свойства дерева). Пусть граф 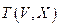имеет n вершин. Тогда следующие утверждения равносильны:
1) Т – дерево (определение)
2) Т не содержит циклов и имеет (n-1) ребер
3) Т – связен и имеет (n-1) ребер
4) Т – связен и каждое его ребро является мостом
5) Любые две вершины графа Т соединены ровно одной простой цепью
6) Т не содержит циклов, но, добавляя в него любое новое ребро, получим граф, содержащий ровно один цикл.
Остовным деревом называется подграф графа G, полученный стиранием ребер из циклов до удаления всех циклов, являющийся деревом.
Полным графом называется граф (без кратных ребер), в которых каждая пара вершин соединена ребром. Число рёбер полного графа равно 
.
Теорема. Число остовных деревьев полного графа 
с n вершинами равно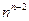 
.
Следствие. Для произвольного простого графа с n вершинами число его остовных деревьев не превосходит числа .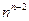
Алгоритм Краскала поиска остовного дерева минимальной длины
Теорема (Краскаль). Пусть 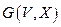– связный граф с n вершинами, на ребрах которого задана неотрицательная числовая функция 
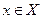, Тогда к построению остовного дерева с минимальной суммой длин ребер приводит следующий алгоритм:
1) Выберем ребро 
графа G, обладающее наименьшей мерой 
, где 
2) По индукции определим последовательность ребер 
выбирая на i -том шаге ребро, отличное от предыдущего и обладающее наименьшей мерой: 
и обладающее тем свойством, что оно не образует циклов с предшествующими ребрами 
3) Полученный таким образом подграф 
графа G и образует остовное дерево наименьшей длины.
|
|
|
