 |
Тема: «Нелинейные регрессионные модели»
|
|
|
|
Индивидуальное задание № 3 по курсу «Эконометрика»
Выполнила:
студентка группы ЗНФ-301
Скворцова Юлия
Последний номер зачетной книжки – 10, вычеркиваем 10 строку.
| t | Y | X1 | X2 | X3 | X4 |
| 30,8 | 459,7 | 39,5 | 55,3 | 79,2 | |
| 31,2 | 492,9 | 37,3 | 54,7 | 77,4 | |
| 33,3 | 528,6 | 38,1 | 63,7 | 80,2 | |
| 35,6 | 560,3 | 39,3 | 69,8 | 80,4 | |
| 36,4 | 624,6 | 37,8 | 65,9 | 83,9 | |
| 36,7 | 666,4 | 38,4 | 64,5 | 85,5 | |
| 38,4 | 717,8 | 40,1 | 93,7 | ||
| 40,4 | 768,2 | 38,6 | 73,2 | 106,1 | |
| 40,3 | 843,3 | 39,8 | 67,8 | 104,8 | |
| 40,4 | 931,1 | 52,1 | 95,4 | 124,1 | |
| 40,7 | 1021,5 | 48,9 | 94,2 | 127,6 | |
| 40,1 | 1165,9 | 58,3 | 123,5 | 142,9 | |
| 42,7 | 1349,6 | 57,9 | 129,9 | 143,6 | |
| 44,1 | 1449,4 | 56,5 | 117,6 | 139,2 | |
| 46,7 | 1575,5 | 63,7 | 130,9 | 165,5 | |
| 50,6 | 1759,1 | 61,6 | 129,8 | 203,3 | |
| 50,1 | 1994,2 | 58,9 | 219,6 | ||
| 51,7 | 2258,1 | 66,4 | 221,6 | ||
| 52,9 | 2478,7 | 70,4 | 168,2 | 232,6 |
Теперь на основании имеющихся данных о потреблении цыплят (Y), среднедушевом доходе (X1), стоимости одного фунта цыплят (X2), стоимости одного фунта свинины (X3) и стоимости одного фунта говядины (X4) построим и сравним уравнения регрессии вида:
1) 
2) 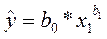
3) 
4) 
РЕШЕНИЕ:
При построении степенных уравнений регрессии использовался пакет SPSS, позволяющий путем применения логарифмического преобразования к объясняемой переменной Y и всем объясняющим переменным Xi линеаризовать модель для нахождения оценок параметров уравнения регрессии с помощью метода наименьших квадратов. Таким образом, были получены следующие модели:
1.  – функция спроса
– функция спроса
Сначала построим линейную регрессию для прологарифмированных исходных переменных:
ln  = ln b0 + b2 ln x2
= ln b0 + b2 ln x2
Обозначим y’ = ln  , b ’ 0 = ln b0, x’2 = ln x2, получим линейную модель: y’ = b ’ 0 + b2 x’2. Найдем для нее оценки параметров b ’ 0, b2. Затем, используя ППП SPSS, получим оценку уравнения регрессии, найденную с помощью метода наименьших квадратов, следующего вида:
, b ’ 0 = ln b0, x’2 = ln x2, получим линейную модель: y’ = b ’ 0 + b2 x’2. Найдем для нее оценки параметров b ’ 0, b2. Затем, используя ППП SPSS, получим оценку уравнения регрессии, найденную с помощью метода наименьших квадратов, следующего вида:
|
|
|
 = 4, 078 * (х2)0, 532
= 4, 078 * (х2)0, 532
 = 2,08; DW = 0,65;
= 2,08; DW = 0,65;  = 0, 1 %.
= 0, 1 %.
Значение t-критерия для проверки значимости коэффициента регрессии 6, 53 (t-табл = 2, 32). Несмотря на то, что все коэффициенты уравнения значимы (t-крит больше t-табл), оно является экономически не интерпретируемым. Это подтверждает положительное значение коэффициента эластичности э2 = 0, 532, из чего следует, что с ростом цены на цыплят на 1 % спрос на них увеличится в среднем на 0, 532 %, что с экономической точки зрения является неверным. В модели не учитывается инфляционный процесс, рост среднедушевых доходов населения, происходящий в стране за рассматриваемые 19 периодов (лет), хотя за это время среднедушевой доход вырос в 5,4 раза, а стоимость цыплят – в 1, 8 раза.
2. 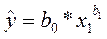 - функция потребления.
- функция потребления.
 = 5, 32 * (х1)0, 283
= 5, 32 * (х1)0, 283
 = 2,144; DW = 0,653;
= 2,144; DW = 0,653;  = 3, 02 %.
= 3, 02 %.
Данная модель интерпретируема. Однако вывод, что при увеличении среднедушевого дохода на 1 % потребление цыплят в среднем растет на 0,283 %, не учитывает динамику цены за рассматриваемый период. Модель характеризуется оценкой остаточной дисперсии  = 2,144, статистикой Дарбина-Уотсона DW = 0,653, которая свидетельствует о положительной автокоррелированности случайных регрессионных остатков.
= 2,144, статистикой Дарбина-Уотсона DW = 0,653, которая свидетельствует о положительной автокоррелированности случайных регрессионных остатков.
3.  – функция спроса-потребления
– функция спроса-потребления
 = 7,515 * (х1)0,428 * (х2)-0,325
= 7,515 * (х1)0,428 * (х2)-0,325
 = 1,247; DW = 1,77;
= 1,247; DW = 1,77;  = 2, 2 %.
= 2, 2 %.
Из модели следует, что с ростом среднедушевого дохода на 1 % при неизменной стоимости цыплят их потребление в среднем увеличится на 0,428% (э1=0,428). В модели, представленной функцией потребления, аналогичный вывод делается на фоне роста стоимости цыплят, чем обусловлена разница в коэффициентах эластичности э1.
Увеличение же стоимости цыплят на 1 % при неизменном среднедушевом доходе приводит к уменьшению потребления в среднем на 0,325 %. Этот вывод интересно сравнивать с выводом, сделанным по модели функции спроса. Если в модели э2 = 0,532 есть парный коэффициент эластичности, то в данной модели э2 = -0,325 – это частный коэффициент эластичности. При этом парный и частный коэффициенты эластичности имеют разные знаки.
|
|
|
Модель функции спроса-потребления обладает хорошими аппроксимирующими свойствами, о чем свидетельствуют статистические характеристики адекватности (средняя ошибка аппроксимации, остаточная дисперсия, статистика Дарбина-Уотсона). Значения критерия Дарбина-Уотсона указывают на отсутствие автокоррелированности остатков.
4.  - функция спроса с учетом цены на товары-заменители
- функция спроса с учетом цены на товары-заменители
Прологарифмировав исходную функцию, получим:
ln  = ln b0 + b2 ln x2 + b3 ln x3 + b4 ln x4.
= ln b0 + b2 ln x2 + b3 ln x3 + b4 ln x4.
Обозначив y’ = ln  , b ’ 0 = ln b0, x’2 = ln x2, x’3 = ln x3, x’4 = ln x4, получим линейную модель:
, b ’ 0 = ln b0, x’2 = ln x2, x’3 = ln x3, x’4 = ln x4, получим линейную модель:
y’ = b ’ 0 + b2 x’2 + b3 x’3 + b4 x’4
Найдем для нее оценки параметров b ’ 0, b2, b3, b4.
Степенная регрессионная модель потребления цыплят с учетом цен на товарозаменители (свинину и говядину) имеет вид:
 = 11,080 * (х2)-0,63 * (х3)0,345 * (х4)0,455
= 11,080 * (х2)-0,63 * (х3)0,345 * (х4)0,455
 = 1,994; DW = 1,7;
= 1,994; DW = 1,7;  = 3, 03 %.
= 3, 03 %.
Модель характеризует зависимость объема потребления от стоимости цыплят (х2) и цены на такие замещающие продукты, как свинина (х3) и говядина (х4). Из модели следует, что при неизменной стоимости двух сопутствующих продуктов увеличение на 1 % стоимости цыплят приводит к снижению их потребления в среднем на 0,63 %.
Увеличение стоимости свинины или говядины на 1% при неизменности цен на остальные входящие в модель продукты приводит к росту потребления цыплят в среднем соответственно на 0,345% и 0,455%.
По рассчитанным характеристикам адекватности, данная модель является менее адекватной, чем модель, построенная в 3-м пункте.
Таким образом, из четырех построенных моделей работоспособны все, кроме первой. Так как исходными при построении модели являются временные ряды годовых данных в реальных ценах, то это не позволяет учесть влияние инфляционных процессов и изменения реальных доходов. В этой связи предпочтение следует отдать двум последним моделям, которые экономически более содержательны и обладают достаточно хорошими статистическими характеристиками.
Заслуживает внимания также модифицированная функция спроса. В этой модели в качестве аргумента выступает переменная  – стоимость 1 фунта цыплят, приходящаяся на единицу среднедушевого дохода. Этот удельный показатель более точно характеризует цену и используется при межстрановых и межрегиональных сопоставлениях цен.
– стоимость 1 фунта цыплят, приходящаяся на единицу среднедушевого дохода. Этот удельный показатель более точно характеризует цену и используется при межстрановых и межрегиональных сопоставлениях цен.
|
|
|
5.  - модифицированная функция спроса
- модифицированная функция спроса

 = 1, 6; DW = 2, 2;
= 1, 6; DW = 2, 2;  = 2, 3 %.
= 2, 3 %.
Статистические характеристики модели свидетельствуют о ее адекватности. Из модели следует, что при увеличении объясняющей переменной на 1 % потребление цыплят снизится на 0, 488 %. Этот вывод согласуется с экономической сущностью явления.
Модель можно представить также в виде:
 = 9,32 * (х1)0,488 * (х2)-0,488
= 9,32 * (х1)0,488 * (х2)-0,488
В таком уравнение сопоставимо с моделью 3, даже по знакам при коэффициентах регрессии. Однако показатели адекватности у этой модели хуже, чем у 3. Последнее можно объяснить тем, что при построении модели 5 на ее параметры было наложено ограничение (дополнительное условие b1 = – b2), что и привело к увеличению остаточной дисперсии.
|
|
|


