 |
Практикум по линейной алгебре
|
|
|
|
Задачи и упражнения к главе 1.
Матрицы и действия над ними. Определитель квадратной матрицы
1.1. Выполнить указанные операции со строками:
a)  б)
б) 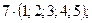
в) 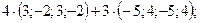 г)
г) 
д) 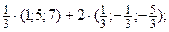 е) (1; 2; 1) + (-1; -1; -2);
е) (1; 2; 1) + (-1; -1; -2);
ж) (1; 1; -3; 2) + (-1; -1; -3; -2);
з) 4 × (4; 1; 2; 0) - 7 × (2; -1; 0; –5);
г) 5 × (-1; 3; -2) - 2 × (5; 0; -5) + 3 × (5; -5; 0).
1.2. Выполнить указанные операции с матрицами:
а) 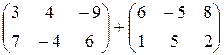 ;
;
б) 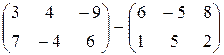 ;
;
в)  ;
;
г)  ;
;
д)  .
.
1.3. Найти матрицу 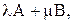 если:
если:
а) 
б) 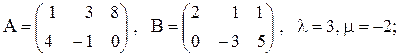
в) 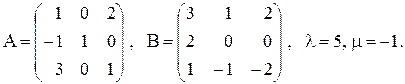
1.4. Образуют ли все геометрические прогрессии с 4 членами линейное пространство?
1.5. Проверьте, что следующие три множества с заданными на них операциями являются линейными пространствами:
а). Множество всевозможных векторов (в трехмерном пространстве или на плоскости) со стандартными операциями сложения и умножения на число.
б). Множество всех многочленов степени, не превышающей k: 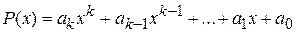 , где a
, где a 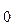 , a
, a  , …, a
, …, a  - произвольные вещественные числа,
- произвольные вещественные числа, 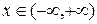 ).
).
Указание. Поскольку произведение многочлена на вещественное число и сумма двух многочленов являются многочленами, остаётся проверить выполнение аксиомам Л1) – Л8).
в). Множество непрерывных на отрезке [ a, b ] функций C [ a, b ].
Указание. Возьмём две непрерывные на [ a, b ] функции f (x), g (x). Так как как сумма непрерывных функций f (x)+ g (x) непрерывна на [ a, b ] и  также непрерывна, то остаётся проверить, что выпонение аксиомам Л1) – Л8).
также непрерывна, то остаётся проверить, что выпонение аксиомам Л1) – Л8).
1.6. Умножить строку на столбец:
1)  ; 2)
; 2)  ;3)
;3) 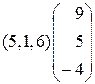 ; 4)
; 4) 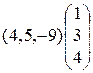 ;
;
5) 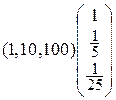 ; 6)
; 6)  ; 7)
; 7)  ;
;
8) 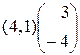 ; 9)
; 9)  ; 10)
; 10)  .
.
1.7. Умножить матрицу на столбец:
1) 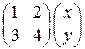 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ; 7)
; 7) 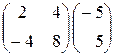 ; 8)
; 8) 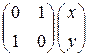 ;
;
9)  ; 10)
; 10) 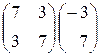 .
.
1.8. Вычислить произведения матриц.
1) 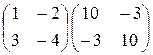 ; 2)
; 2) 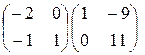 ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6) 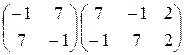 ; 7)
; 7) 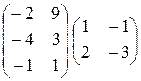 ; 8)
; 8)  ;
;
9) 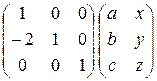 ; 10)
; 10) 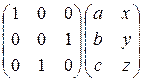 ; 11)
; 11) 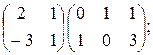
12) 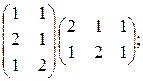 13)
13)  14)
14) 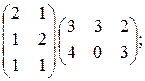
15)  ; 16)
; 16)  ; 17)
; 17)  ;
;
18)  ; 19)
; 19) 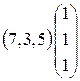 ; 20)
; 20) 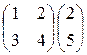 ;
;
21) 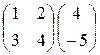 ; 22)
; 22) 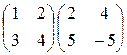 ;
;
23)  ; 24)
; 24)  ;
;
25) 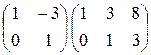 .
.
1.9.
Вычислить 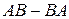 , если
, если
1) 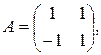
 2)
2) 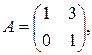
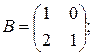
3) 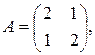
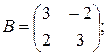 4)
4) 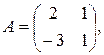

5) 
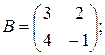 6)
6) 
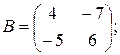
7) 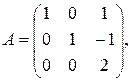

8) 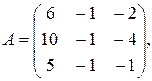

9) 

10) 

11) Случайно ли на главной диагонали в задачах 1)-6) получаются взаимно противоположные числа?
|
|
|
1.10. Выполнить операции с матрицами:
1) 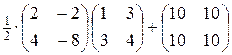 ; 2)
; 2) 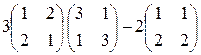 ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7) 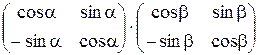 ; 8)
; 8) 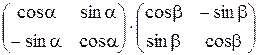 .
.
1.11. Вычислить произведения матриц:
1).  ; 2)
; 2)  ;
;
3) 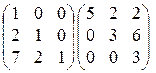 ; 4)
; 4) 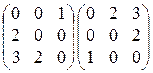 ;
;
5) 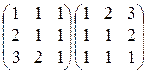 ; 6)
; 6) 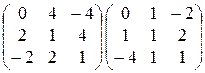 ;
;
7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10) 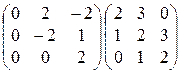 ;
;
11)  ; 12)
; 12) 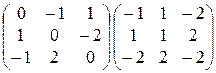 ;
;
13) 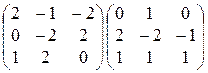 ; 14)
; 14)  ;
;
15) 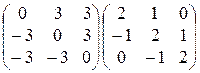 ; 16)
; 16)  ;
;
17)  ; 18)
; 18) 
19)  ; 20)
; 20) 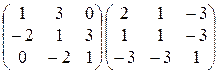 ;
;
21) 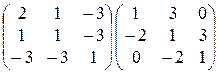 ; 22)
; 22) 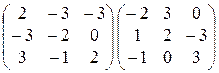 ;
;
23) 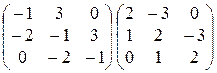 ; 24)
; 24) 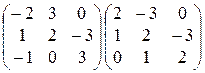 ;
;
25) 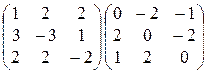 ; 26)
; 26) 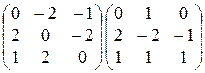 ;
;
27)  ; 28)
; 28)  ;
;
29) 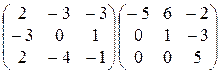 .
.
1.12. Положим 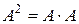 ,
, 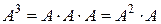 ,...,
,..., 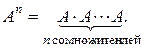 .
.
Вычислить: 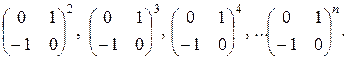
1.13. Проверить, что 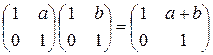 .
.
1.14. Вычислить: а)  ; б)
; б) 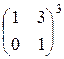 ; в)
; в) 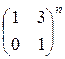 .
.
1.15. Пусть  Найти
Найти 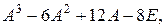 где
где 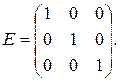
1.16. Найти значение многочлена  , если:
, если:
а) 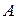 =
=  ;
; 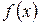 =
=  =
=  ;
;
б) 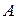 =
=  ;
; 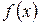 =
=  ;
;
в) 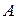 =
=  ;
; 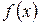 =
=  ;
;
г) 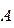 =
= 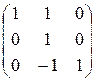 ;
; 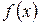 =
=  .
.
1.17. Даны матрицы 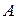 и
и  Вычислить матрицу
Вычислить матрицу 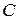 , если:
, если:
1). 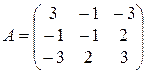 ;
; 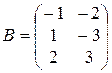 ;
; 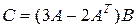 .
.
2).  ;
; 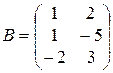 ;
; 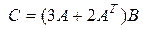 .
.
3).  ;
;  ;
;  .
.
4). 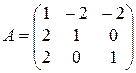 ;
; 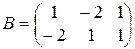 ;
; 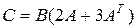 .
.
5).  ;
; 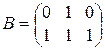 ;
;  .
.
6) 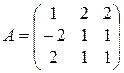 ;
; 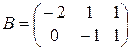 ;
; 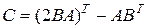 .
.
7). 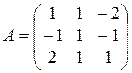 ;
;  ;
; 
8).  ;
;  ;
;  .
.
9).  ;
;  ;
; 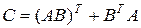 .
.
10).  ;
; 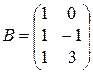 ;
; 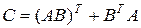 .
.
11). 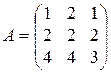 ;
;  ;
;  .
.
12).  ;
; 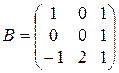 ;
;  .
.
13).  ;
; 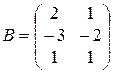 ;
;  .
.
14).  ;
; 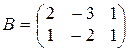 ;
; 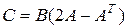 .
.
15). 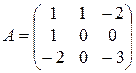 ;
;  ;
; 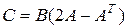 .
.
1.18. Приведите пример, показывающий, что произведение матриц некоммутативно.
1.19. Придумайте условие, при котором для двух матриц A и B справедливы формулы разности квадратов, квадрата разности и квадрата суммы: 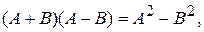
 ,
, 
 . Верны ли эти формулы для двух произвольных квадратных матриц одного порядка.
. Верны ли эти формулы для двух произвольных квадратных матриц одного порядка.
1.20. Вычислить определители:
1) 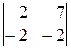 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 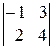 ; 5)
; 5)  ; 6)
; 6) 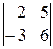 ;
;
7) 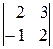 ; 8)
; 8)  ; 9)
; 9)  ; 10)
; 10)  ;
; 
11) 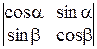 .
.
1.21. Вычислить определители по правилу треугольников или правилу Саррюса:
1). 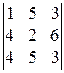 . 2).
. 2).  . 3).
. 3).  .
.
4). 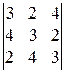 . 5).
. 5).  . 6).
. 6).  .
.
7). 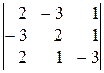 . 8).
. 8). 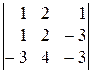 . 9).
. 9).  .
.
10. 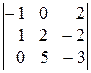 . 11).
. 11).  .
.
12). 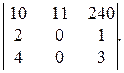
1.22. Вычислить определители разложением по строке (столбцу).
1). 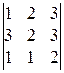 . 2).
. 2).  . 3).
. 3). 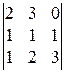 . 4).
. 4). 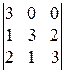 .
.
5).  . 6).
. 6). 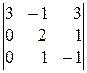 . 7).
. 7).  .
.
8).  . 9).
. 9).  . 10).
. 10).  .
.
1.23. Вычислить определители, используя их свойства.
1). 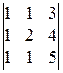 . 2).
. 2). 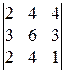 . 3).
. 3).  . 4).
. 4). 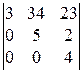 .
.
5).  . 6).
. 6).  . 7).
. 7). 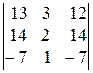 . 8).
. 8).  .
.
9).  . 10).
. 10).  . 11).
. 11).  .
.
12).  .
.
1.24. Числа 551, 377и 319 кратны числу 29. Докажите, что определитель 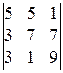 делится на 29 без остатка, не вычисляя этот определитель.
делится на 29 без остатка, не вычисляя этот определитель.
1.25. Докажите, что определитель 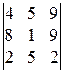 делится на 2, на 9 и на 18 без остатка, не вычисляя этот определитель.
делится на 2, на 9 и на 18 без остатка, не вычисляя этот определитель.
1.26. Числа 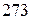 ,
,  и
и  кратны числу
кратны числу  . Не вычисляя определитель
. Не вычисляя определитель  , докажите, что
, докажите, что 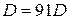 и, следовательно,
и, следовательно,  .
.
1.27. Элементами матрицы знаков алгебраических дополнений служат знаки «плюс» и «минус», причем в  –й строке на
–й строке на  –м месте стоит «плюс», если
–м месте стоит «плюс», если 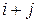 –четное число, в противном случае – знак «минус». Составьте такую матрицу порядка: 1) три; 2) четыре; 3) пять.
–четное число, в противном случае – знак «минус». Составьте такую матрицу порядка: 1) три; 2) четыре; 3) пять.
В задачах 1.28.–1.29 определители можно вычислить, применяя разложение по строке (столбцу), преобразуя определители с помощью элементарных преобразований строк и используя их свойства.
|
|
|
Элементарные преобразования строк:
1) перемена двух строк местами;
2) прибавление к одной из строк определителя другой строки, умноженной на некоторое число;
3) умножение некоторой строки определителя на число, не равное нулю.
Напомним, что при преобразовании первого типа, определитель меняет свой знак; при преобразовании второго типа не меняется; и при преобразовании третьего типа, определитель умножается на то число, на которое была умножена строка.
1.28. Вычислить определители:
1).  ; 2).
; 2). 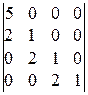 ; 3).
; 3).  ;
;
3). 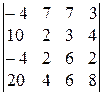 ; 5).
; 5).  ; 6).
; 6). 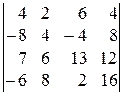 ;
;
7).  ; 8).
; 8). 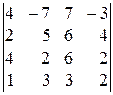 ; 9).
; 9). 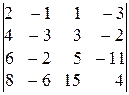 ;
;
10). 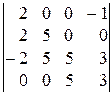 ; 11).
; 11). 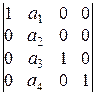 ; 12)
; 12) 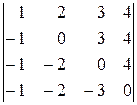
1.29. Вычислить определители:
1).  ; 2).
; 2).  ; 3).
; 3). 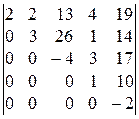 ; 4).
; 4). 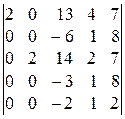 ; 5).
; 5). 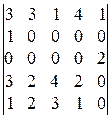 ; 6).
; 6). 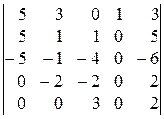 ;
;
7).  ; 8).
; 8).  ;
;
9). 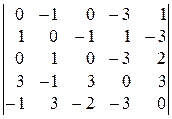 ; 10).
; 10). 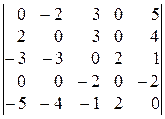 ;
;
11).  ; 12).
; 12). 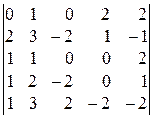 ;
;
13).  ; 14).
; 14). 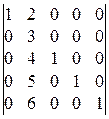 ;
;
15).  ; 16).
; 16). 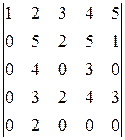 .
.
1.30. Разложите определитель
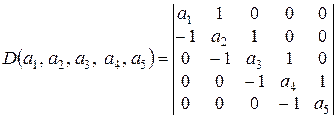
1) по первому столбцу (строке);
2) по последнему столбцу (строке).
1.31. Какие из следующих бинарных отношений являются подстановками:
1)  , 2)
, 2)  , 3)
, 3) 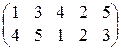 , 4)
, 4)  ?
?
1.32. Найти знак перестановки двумя способами (по числу инверсий и при помощи транспозиций):
1). 3 2 1; 2). 2 3 1 4; 3). 3 1 2 4; 4). 2 4 1 3; 5). 5 2 3 4 1; 6). 1 4 3 2 5;
7). 6 7 2 5 1 3 4; 8). 7 2 3 1 5 4 6; 9). 6 5 3 1 2 4 7; 10). 5 3 4 7 6 1 2.
1.33. а). Найдите число инверсий в подстановке, определите ее четность и знак по числу инверсий.
б). Представьте подстановку в виде произведения независимых циклов, определите ее четность и знак по декременту.
в). Определите четность подстановки и её знак при помощи транспозиций.
1). 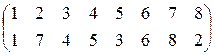 ; 2).
; 2). 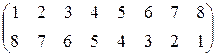 ;
;
3). 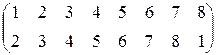 ; 4).
; 4). 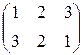 ; 5).
; 5).  ;
;
6). 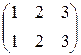 ; 7).
; 7).  ;
;
8). 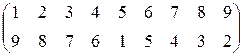 9).
9).  ;
;
10). 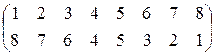 .
.
1.34. С какими знаками входят данные произведения в определители соответствующих порядков:
1). 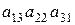 ; 2).
; 2). 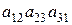 ; 3).
; 3). 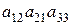 ; 4).
; 4). 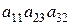 ; 5).
; 5). 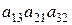 ;
;
6). 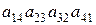 ; 7).
; 7). 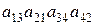 ; 8).
; 8). 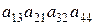 ; 9).
; 9). 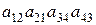 ;
;
10).  ; 11).
; 11).  ; 12).
; 12). 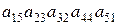 ;
;
13). 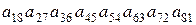 ; 14).
; 14).  ; 15).
; 15). 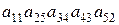 ?
?
1.35. Найти определитель, вычислив знак соответствующей подстановки
1). 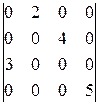 ; 2).
; 2).  ; 3).
; 3).  ; 4).
; 4).  ;
;
5).  ; 6).
; 6).  ; 7).
; 7). 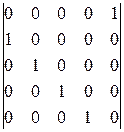 ;
;
8). 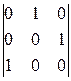 ; 9).
; 9). 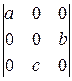 .
.
1.36. Найдите обратные подстановки:
1).  , 2).
, 2). 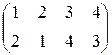 , 3).
, 3).  .
.
1.37. Пусть  – подстановка
– подстановка 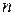 -ой степени, такая что
-ой степени, такая что  . Вычеркнем в этой подстановке столбец
. Вычеркнем в этой подстановке столбец 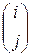 . Затем в верхней строке уменьшим все числа, большие числа
. Затем в верхней строке уменьшим все числа, большие числа 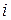 , на единицу. И, наконец, в нижней строке уменьшим все числа, большие числа
, на единицу. И, наконец, в нижней строке уменьшим все числа, большие числа  , на единицу. Получим подстановку
, на единицу. Получим подстановку 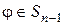 . Покажите, что
. Покажите, что 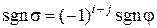 . Выполните указанную операцию с последним столбцом подстановки
. Выполните указанную операцию с последним столбцом подстановки 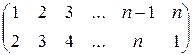 .
.
1.38. Пусть  Рассмотрим следующие подстановки
Рассмотрим следующие подстановки 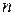 -ой степени
-ой степени
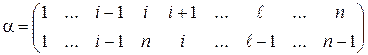 и
и
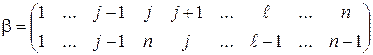 .
.
Обозначим через 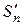 множество подстановок из
множество подстановок из 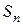 таких, что
таких, что 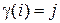 и рассмотрим взаимно однозначное отображение
и рассмотрим взаимно однозначное отображение 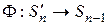 такое, что
такое, что  является результатом удаления последнего столбца
является результатом удаления последнего столбца 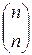 подстановки
подстановки  для любой подстановки
для любой подстановки  .
.
|
|
|
Докажите, что подстановки 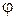 в разложении минора
в разложении минора  могут быть получены из соответствующих подстановок по правилу
могут быть получены из соответствующих подстановок по правилу 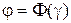 . Это правило позволяет поставить в соответствие члену определителя
. Это правило позволяет поставить в соответствие члену определителя  , содержащему
, содержащему 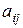 в качестве сомножителя, элемент минора
в качестве сомножителя, элемент минора  :
:
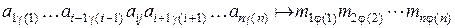 .
.
Докажите, что это соответствие является взаимно однозначным. 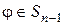 . Докажите, что
. Докажите, что 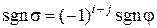 . Используя отображение
. Используя отображение 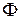 , докажите теорему о разложении определителя по строке (столбцу).
, докажите теорему о разложении определителя по строке (столбцу).
1.39. Докажите, что определитель, элементы двух строк (столбцов) которого соответственно пропорциональны, равен нулю.
1.40. Матрица называется кососимметрической, если 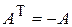 . Чему равен определитель кососимметрической матрицы нечётного порядка?
. Чему равен определитель кососимметрической матрицы нечётного порядка?
1.41. Чему равен определитель, если сумма его строк с четными номерами равна сумме его строк с нечетными номерами?
1.42. Чему равен определитель, одна строка которого равна сумме всех остальных строк?
1.43. Пусть 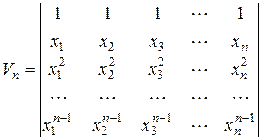 – определитель Вандермонда. Доказать, что
– определитель Вандермонда. Доказать, что 
Ответы на задачи к главе 1
1.1. a) 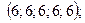 б)
б) 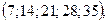 в)
в) 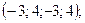 г)
г)  д)
д)  .
.
1.2. а) 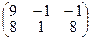 ; б)
; б)  в)
в) 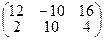 ; г)
; г) 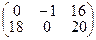 ;
;
д)  .
.
1.3. a) 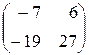 ; б)
; б)  ; в)
; в) 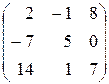 .
.
1.4. Нет.
1.6. 1) 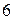 ; 2)
; 2) 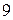 ; 3)
; 3) 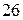 ; 4)
; 4)  ; 5)
; 5) 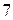 ;
;
6) 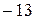 ; 7)
; 7)  ; 8)
; 8) 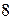 ; 9)
; 9) 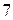 ; 10)
; 10)  .
.
1.7. 1) 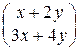 ; 2)
; 2) 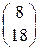 ; 3)
; 3)  ; 4)
; 4) 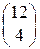 ; 5)
; 5) 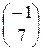 ;
;
6) 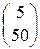 ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  ; 10)
; 10)  .
.
1.8. 1)  ; 2)
; 2) 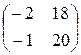 ; 3)
; 3) 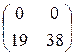 ; 4)
; 4) 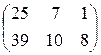 ;
;
5) 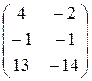 ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8) 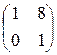 ;
;
9) 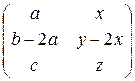 ; 10)
; 10)  ; 11)
; 11) 
12). 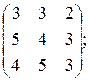 13)
13) 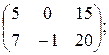 14)
14) 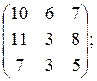
15) 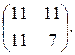 16)
16) 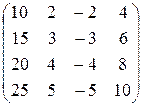 ; 17)
; 17) 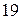 ; 18)
; 18) 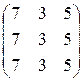 ;
;
19)  . 20)
. 20) 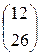 ; 21)
; 21) 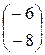 ; 22)
; 22) 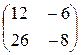 ; 23)
; 23)  ;
;
24) 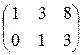 ; 25)
; 25) 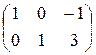 .
.
1.9.
1) 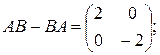 2)
2) 
3) 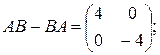 4)
4) 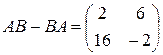 ;
;
5) 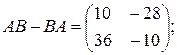 6)
6) 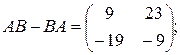
7)  8)
8) 
9) 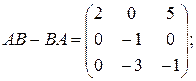 10)
10)  .
.
11). Следующая формула показывает, что не случайно.
Если 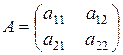 ,
, 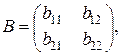 то
то 

1.10. 1) 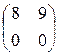 ; 2)
; 2) 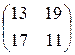 ; 3)
; 3)  ; 4)
; 4) 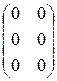 ;
;
5) 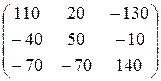 ; 6)
; 6) 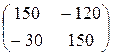 ;
;
7)  ; 8)
; 8)  .
.
1.11.
1)  2)
2)  3)
3) 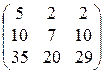 4)
4) 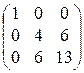 5)
5)  6)
6)  7)
7) 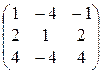 8)
8)  9)
9) 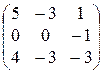 10)
10)  11)
11)  12)
12)  13)
13) 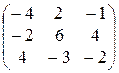 14)
14)  15)
15) 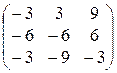 16)
16) 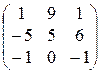 17)
17)  18)
18)  19)
19)  20)
20) 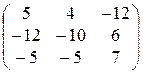 21)
21) 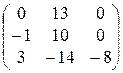 22)
22)  23)
23)  24)
24) 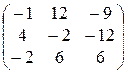 25)
25)  26)
26) 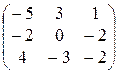 27)
27)  28)
28)  29)
29) 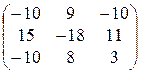 .
.
1.14. а)  б)
б) 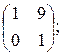 в)
в) 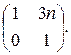
1.15. 
1.16. а)  ; б)
; б) 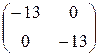 ; в)
; в) 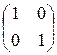 ; г)
; г) 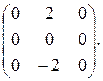
1.17. 1).  ; 2).
; 2).  ; 3).
; 3).  ; 4).
; 4). 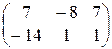 ; 5).
; 5). 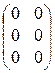 ; 6).
; 6). 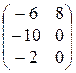 ; 7).
; 7).  ; 8).
; 8). 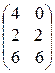 ; 9).
; 9).  ; 10).
; 10).  ; 11).
; 11). 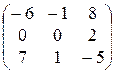 ; 12).
; 12).  ; 13).
; 13). 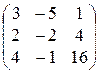 ; 14).
; 14). 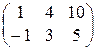 ; 15).
; 15).  .
.
1.20. 1). 10; 2). 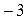 ; 3) 3; 4)
; 3) 3; 4)  ; 5). 1; 6). 27; 7). 7; 8). 17.
; 5). 1; 6). 27; 7). 7; 8). 17.
9).  ; 10).
; 10). 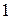 ; 11).
; 11). 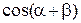 .
.
1.21. 1). 72; 2)  ; 3). 9; 4). 27; 5).
; 3). 9; 4). 27; 5). 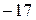 ; 6).
; 6). 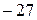 ; 7). 0; 8). 40; 9).
; 7). 0; 8). 40; 9). 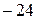 ; 10). 6;
; 10). 6;
11). 20. 12). –22.
1.22. 1).  ; 2). 3; 3).
; 2). 3; 3). 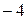 ; 4). 21; 5). 0;
; 4). 21; 5). 0;
6). 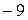 ; 7). 10; 8). 12; 9). 20; 10).
; 7). 10; 8). 12; 9). 20; 10). 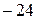 .
.
1.23. 1). 2. 2). 0. 3). 0. 4). 60. 5). 12. 6) 6. 7). 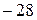 . 8). 0. 9). 0.
. 8). 0. 9). 0.
10). 198. 11).  . 12).
. 12). 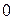 .
.
1.24. 1). 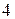 ; 2).
; 2). 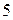 ; 3).
; 3). 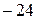 ; 4).
; 4). 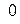 ; 5).
; 5). 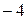 ;
;
6). 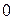 ; 7).
; 7). 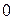 ; 8).
; 8). 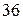 ; 9).
; 9). 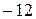 ; 10).
; 10). 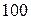 ; 11).
; 11).  .
.
12). 24.
1.29. Указание. Практическое значение теоремы о разложении определителя по строке (столбцу) заключается в следующем. Используя свойства определителей, получаем нули в какой-нибудь строке или столбце определителя n -го порядка Затем применяя о разложении определителя по строке (столбцу), переходим к определителю, порядок которого на единицу меньше. В свою очередь, определитель (п – 1)-го порядка можно свести к определителю (п – 2)-го порядка и т. д., пока задача не сведется к определителю третьего или второго порядка.
|
|
|
1) . – 56.Указание.Сведем вычисление определителя 5-го порядка 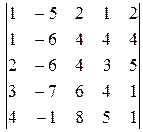 к вычислению определителя 4-го порядка. Вычтем из третьего столбца определителя его удвоенный первый столбец
к вычислению определителя 4-го порядка. Вычтем из третьего столбца определителя его удвоенный первый столбец
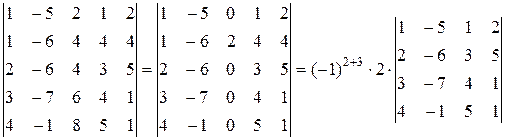 .
.
2). 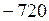 ; 3).
; 3). 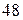 ;
;


