Вывод характеристического уравнения замкнутой системы.

АФЧХ замкнутых и разомкнутых (статических и астатических) систем.

Для того чтобы оценить количественно меру устойчивости, можно применить критерий предложенный в 1932 году американцем Найквистом. Критерий Найквиста позволяет судить об устойчивости замкнутых систем по АФЧХ разомкнутых систем. По этому критерию система устойчива, если АФЧХ разомкнутой системы не охватывает точку (-1;j) и не устойчива, если охватывает.

Рассмотрим функциональную схему в общем виде. Если какая- либо точка АФЧХ такой системы имеет координату (-1;0), то это значит, что входной сигнал появится на выходе с той же амплитудой, но будет, сдвинут на 180 градусов., то есть, станет сигналом положительной обратной связи. Так как амплитуда не уменьшилась, то возникнут незатухающие колебания, при выходе влево за точку (-1;0) имеем усиление ПОС.

 

Если разомкнутая система неустойчива, а АФЧХ несколько раз пересекает ось Re.

В этом случае вводится определение: положительный переход – переход вниз через ось слева от –1 с ростом частоты. Отрицательный переход – переход вверх через ось с ростом частоты. Система устойчива, если суммарное количество (разность) положительных и отрицательных переходов равно m/2, где m – число положительных корней разомкнутой системы.

Лучше всего это определение может быть понято по представлению в графическом виде.

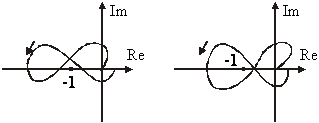
Если система астатическая, то её характеристическое уравнение имеет нулевые корни, АФЧХ разомкнутой системы при =0 уходит в бесконечность в квадранте с номером, равном порядку астатизма системы. Если окружность бесконечного радиуса охватывает точку (-1;0), то система неустойчива, если не охватывает, то устойчива.

1- первый прядок, устойчива;

2- второй порядок, неустойчива;

3- третий порядок, устойчива.

Теория устойчивости, теоремы Ляпунова, косвенные критерии определения устойчивости.

Устойчивость — свойство САУ возвращаться в заданный или близкий к нему установившийся режим после какого-либо возмущения.

Устойчивая САУ — система, в которой переходные процессы являются затухающими.

— операторная форма записи линеаризированного уравнения.

y(t) = y _уст (t)+y _п = y _вын (t)+y _св

y _уст (y _вын) — частное решение линеаризированного уравнения.

y _п (y _св) — общее решение линеаризированного уравнения как однородного дифференциального уравнения, то есть

САУ устойчива, если переходные процессы у_n(t), вызываемые любыми возмущениями, будут затухающими с течением времени, то есть при

Решая дифференциальное уравнение в общем случае, получим комплексные корни p_i, p_i+1 = ±α_i ± jβ_i

Каждой паре комплексно-сопряженных корней соответствует следующая составляющая уравнения переходного процесса:

, где ,

Из полученных результатов видно, что:

при ∀α_i<0 выполняется условие устойчивости, то есть переходный процесс с течением времени стремится к у_уст (Теорема Ляпунова 1);

при ∃α_i>0, выполняется условие неустойчивости (Теорема Ляпунова 2), то есть 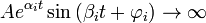, что приводит к расходящимся колебаниям;

при ∃α_i=0 и ∃α_i>0 , что приводит к незатухающим синусоидальным колебаниям системы (система на границе устойчивости) (Теорема Ляпунова 3).

Вывод характеристического уравнения замкнутой системы.

Характеристическое уравнение системы может быть получено как из дифференциального уравнения системы относительно выходной величины, так и из любой передаточной функции замкнутой системы. Все передаточные функции замкнутой системы относительно выходной величины, ошибки и возмущения имеют общий знаменатель - , который является характеристическим полиномом системы, а уравнение D(p)=0 – есть характеристическое уравнение системы.

Характеристическое уравнение полученной замкнутой системы определяется следующим образом:

D(p) = det|pI – F|

где I — единичная матрица размерности nxn.

Поскольку собственные числа матрицы однозначно определяют коэффициенты характеристического полинома, задача может быть сформулирована следующим образом: для управляемой системы (3.1) с характеристическим полиномом 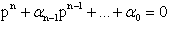найти вектор L коэффициентов обратных связей и предварительный коэффициент усиления K, чтобы замкнутая система имела желаемую стандартную форму характеристического полинома с заданными коэффициентами l _i.

Поделиться:

Воспользуйтесь поиском по сайту: