 |
Интегрирование рациональных функций.
|
|
|
|
Интегрирование неопределенного интеграла методом подстановки.
Неопределенный интеграл.
Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) + C.
Записывают: 
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Свойства:
1. 
2. 
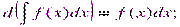
3. 
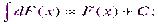
4. 
где u, v, w – некоторые функции от х.
Способ подстановки (замены переменных).
Теорема: Если требуется найти интеграл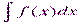 
(t)dt получается:¢j(t) и dx = j, но сложно отыскать первообразную, то с помощью замены x =
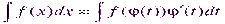
Доказательство: Продифференцируем предлагаемое равенство:
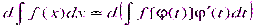
По рассмотренному выше свойству №2 неопределенного интеграла:
f(x)dx = f[j(t)]¢j(t)dt
что с учетом введенных обозначений и является исходным предположением. Теорема доказана.
Пример. Найти неопределенный интеграл 
.
Сделаем замену t = sinx, dt = cosxdt.
Пример. 
Замена
Получаем:
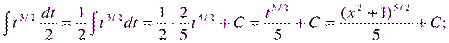
Интегрирование неопределенного интеграла по частям.
Интегрирование по частям.
Способ основан на известной формуле производной произведения:
u¢v + v¢ = u¢(uv)
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав, получаем: 
, а в соответствии с приведенными выше свойствами неопределенного интеграла:
или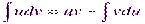 
;
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Пример. 
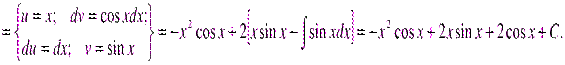
Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.
Пример.
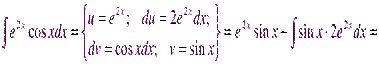
Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.
|
|
|
Таким образом, интеграл найден вообще без применения таблиц интегралов.
Интегрирование рациональных функций.
Функция 
называется рациональной, если она вычисляется с помощью четырех арифметических действий, то есть в общем случае является частным от деления двух многочленов: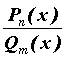 
. Если 
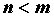, рациональная дробь называется правильной. Неопределенный интеграл от рациональной функции всегда можно вычислить. Для этого:
Если 
, выделяем целую часть рациональной дроби с помощью деления многочлена на многочлен. Правильную рациональную дробь (или правильный остаток от деления) раскладываем на простейшие дроби. Вид
Если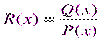 
- правильная рациональная дробь, знаменатель P(x) которой представлен в виде произведения линейных и квадратичных множителей (отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: P(x) = (x - a)a…(x - b)b(x2 + px + q)l…(x2 + rx + s)m ), то эта дробь может быть разложена на элементарные по следующей схеме:
где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины.
При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин Ai, Bi, Mi, Ni, Ri, Si применяют так называемый метод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.
Применение этого метода рассмотрим на конкретном примере.
Пример.
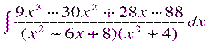
Т.к. (
, то
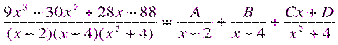
Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:
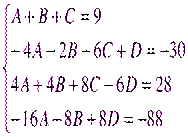
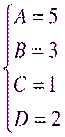
Итого:
Пример.
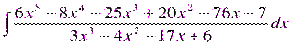
Т.к. дробь неправильная, то предварительно следует выделить у нее целую часть:
|
|
|
Разложим знаменатель полученной дроби на множители. Видно, что при х = 3 знаменатель дроби превращается в ноль.
Таким образом:
3x3 – 4x2 – 17x + 6 = (x – 3)(3x2 + 5x – 2) = (x – 3)(x + 2)(3x – 1).
Тогда:
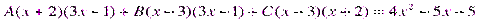
Для того, чтобы избежать при нахождении неопределенных коэффициентов раскрытия скобок, группировки и решения системы уравнений (которая в некоторых случаях может оказаться достаточно большой) применяют так называемый метод произвольных значений. Суть метода состоит в том, что в полученное выше выражение подставляются поочередно несколько (по числу неопределенных коэффициентов) произвольных значений х. Для упрощения вычислений принято в качестве произвольных значений принимать точки, при которых знаменатель дроби равен нулю, т.е. в нашем случае – 3, -2, 1/3. Получаем:
Окончательно получаем: 
= 
|
|
|
