Описание лабораторной установки

Пенза 2003

УДК 531.23

ББК 22я7

И39

Рекомендовано Редсоветом университета

 

Рецензент –

кандидат физико-математических наук, доцент И.Д.Караман

 

 

 

И39

 

 

Изучение вращательного движения с помощью маятника Обербека и его компьютерного имитатора: Методические указания к лабораторной работе № 9
/ Г.И.Грейсух, С.А.Степанов, С.В.Голобоков. – Пенза: ПГУАС, 2003. – 16 с.

 

 

Изложены основные положения кинематики и динамики твер­дого тела. Приведена методика и описан эксперимент по проверке основного закона динамики вращательного движения. Эксперимент может быть выполнен как на реальной лабораторной установке (маятнике Обербека), так и на ее компьютерном имитаторе.

Методические указания подготовлены на кафедре физики и пред­назначены для студентов тех специальностей, учебные планы которых предусматривают изучение курса физики.

 

© Пензенский государственный университет

архитектуры и строительства, 2003

© Г.И.Грейсух, С.А.Степанов,

С.В.Голобоков, 2003

Цель работы - проверка основного закона динамики вращательного движения и определение момента инерции маятника Обербека.

Приборы и принадлежности: лабораторная установка, включающая маятник Обербека, линейку, набор гирей различной массы, секундомер, штангенциркуль, а также IBM-совместимый персональный компьютер и пакет компьютерных программ, имитирующих работу лабораторной установки.

 

ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

При изучении различных видов движения протяженных тел широко используется физическая модель абсолютно твердого тела. В рамках этой модели полагают, что действие сил на тело не приводит к его деформации, а влияет лишь на особенности движения тела. В дальнейшем для краткости такую модель будем называть просто «твердым телом».

Чтобы указать положение твердого тела в пространстве, необходимо зафиксировать какие-либо три его точки, не лежащие на одной прямой. Эти три точки описываются девятью координатами, между которыми имеются три соотношения, выражающие постоянство расстояний между точками твердого тела. Следовательно, в общем случае движение твердого тела - это движение с шестью степенями свободы.

Простейшими видами движения твердого тела являются посту­пательное и вращательное движения. Поступательным называ­ется дви­жение, при котором любая прямая, жестко связанная с дви­жущимся телом, остается параллельной своему первоначаль­ному положению. Вращательное движение - это такой вид дви­жения, при котором по крайней мере две точки тела остаются непо­движ­ными. Прямая, проходящая через эти точки, называется осью вращения. Все точки твердого тела, лежащие на оси вращения, неподвижны, другие его точки движутся по окружностям в плоскос­тях, перпендикулярных оси вращения. Центры этих окружностей лежат на оси вращения.

Вращательное движение можно рассматривать как движение с одной степенью свободы, если ввести угловую координату j, т.е. угол между двумя плоскостями, проходящими через ось вращения. Одна из этих плоскостей зафиксирована в пространстве, а вторая - жестко связана с телом. При этом для определенности полагают, что в начальный момент времени эти плоскости совпадают, т.е. j₀=0.

 

 

Быстроту вращения тела характеризуют угловой скоростью

, (1)

а быстроту изменения угловой скорости – угловым ускорением

. (2)

Для того чтобы изменить угловую скорость тела, к нему необходимо приложить вращающий момент – величину, харак­теризующую вращательный эффект силы F при ее воздействии на твердое тело. Вращающий момент численно равен

, (3)

где – плечо силы – кратчайшее расстояние от оси вращения до линии действия силы.

Тело, обладая инертностью, противодействует изменению его скорости. Момент инерции – это мера инертности тела при его вращательном движении. Эта величина зависит от массы, формы и размеров тела, а также от расположения оси вращения. Кроме того, для неоднородных тел момент инерции зависит от того, как распределена плотность вещества по объему тела.

Обычно момент инерции различных тел приводят относительно оси, проходящей через центр их инерции. Например, момент инерции однородного стержня относительно оси, проходящей через его центр перпендикулярно оси стержня, определяется формулой

, (4)

где и –соответственно масса и длина стержня.

Если же необходимо рассчитать момент инерции I относительно оси, не проходящей через центр инерции тела, то используют теорему Штейнера, связывающую моменты инерции относительно двух параллельных осей, одна из которых проходит через центр инерции тела:

, (5)

где – масса тела;

– расстояние между параллельными осями.

Из формулы (5), в частности, следует, что если тело движется по окружности радиусом 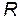и размерами тела можно пренебречь (), то его момент инерции

. (6)

Иногда говорят, что формула (6) определяет момент инерции частицы (материальной точки), движущейся по окружности.

Ниже приведены моменты инерции некоторых однородных тел правильной геометрической формы:

- сплошного цилиндра относительно продольной оси

; (7)

- полого цилиндра относительно продольной оси

; (8)

- шара относительно оси, проходящей через его центр

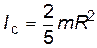. (9)

Часто при расчете момента инерции оказывается полезным ис­пользовать его свойство аддитивности: момент инерции составного тела равен сумме моментов инерции его отдельных частей:

. (10)

В соответствии с законом динамики вращательного движения угло­вое ускорение тела пропорционально результирующему вращаю­щему моменту всех сил, приложенных к телу, и обратно пропорционально моменту инерции тела, т.е.

. (11)

Результирующий вращающий момент находится как алгеб­раи­ческая сумма всех вращающих моментов, приложенных к телу. Вращающие моменты, стремящиеся повернуть тело против часовой стрел­ки, считаются положительными, по часовой стрелке – отриц­ательными. В зависимости от их соотношения угловое ускорение также может быть положительным или отрицательным.

Закон, выражаемый формулой (11), при изучении вращения тел играет ту же роль, что и второй закон Ньютона в динамике частиц.

ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ

Внешний вид лабораторной установки представлен на рис. 1. Маятник Обербека состоит из двух стержней 1 длиной и массой , закрепленных на валу 2 так, что ось вращения проходит через центр тяжести системы. На концах стержней укреплены четыре одинаковых груза 3 массой 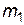на расстоянии 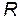от оси вращения. На валу 2 имеются два барабана 4 радиусами и , на которые наматывается шнур 5. Шнур перекинут через ролик 7. К сво­бодному концу шнура прикрепляется гиря 6 массой . Вал 2 свободно вращается благодаря подшипникам, закрепленным в раме установки.

 

 

Рис. 1

Вращая маятник Обербека, наматывают шнур 5 на барабан 4. При этом гиря 6 поднимается на некоторую высоту . Если осво­бодить систему, то гиря под действием силы тяжести будет опус­кать­ся вниз. Сила натяжения нити передается барабану и создает вра­щающий момент, под действием которого маятник начинает вращаться. Время падения гири определяется по секун­домеру, вы­со­та падения – линейкой, размеры деталей маятника – штанген­цир­ку­лем.

МЕТОДИКА ЭКСПЕРИМЕНТА

В ходе эксперимента проверяется основной закон динамики вра­щательного движения путем сравнения расчетного и экспери­мен­тально полученного значений момента инерции маятника Обербека.

Расчетное значение момента инерции маятника получают как сумму моментов инерции всех его деталей:

, (12)

где – момент инерции груза;

– момент инерции стержня.

Пренебрегая размерами груза по сравнению с радиусом вращения и используя формулу (6), найдем момент инерции груза относительно оси вращения:

, (13)

где 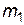– масса груза;

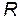– расстояние от центра груза до оси вращения.

Из рис. 1 видно, что расстояние от центра груза до оси вра­щения

, (14)

где – длина стержня;

– длина груза.

Момент инерции стержня относительно оси, проходящей через центр тяжести, определяется формулой (4):

, (15)

где – масса стержня.

Подставляя выражения (13) и (15) в уравнение (12), получим, что расчетное значение момента инерции маятника Обербека можно вычислить по формуле

. (16)

Для получения экспериментального значения момента инерции маятника Обербека рассмотрим действие сил, вызывающих его вращение. На маятник действуют сила тяжести, сила реакции опор подшипников и сила натяжения нити. Кроме того, со стороны подшипников на вращающуюся ось действуют силы трения. Сила тяжести и сила реакции опор, проходя через ось вращения, вращающих моментов не создают. Сила натяжения нити F пере­дается ободу барабана и создает вращающий момент М. Силы трения создают тормозящий момент , препятствующий вра­ще­нию маятника (рис. 2а).

Под действием постоянных вращающего и тормозящего момен­тов маятник Обербека будет вращаться равноускоренно с угловым ускорением a. Основной закон динамики его вращательного движения, согласно уравнению (11), запишется в виде

. (17)

Вращающий момент связан с силой натяжения нити и радиусом барабана соотношением

. (18)

Для нахождения силы натяжения нити решим задачу динамики поступательно движущейся гири. На нее действуют две силы: сила тяжести m g, направленная вертикально вниз, и сила натяжения нити F, направленная вертикально вверх (рис. 2б). В соответствии со вторым законом Ньютона имеем

m g + F = m a. (19)

 

а б

 

 

Рис. 2

 

Проецируя уравнение (19) на ось Y, получим:

, (20)

где – ускорение свободного падения.

Ускорение гири можно определить из формулы пути рав­но­ускоренного падения без начальной скорости: , откуда

. (21)

Из уравнений (20) и (21) получим, что сила натяжения нити

, (22)

а вращающий момент

. (23)

Как известно, угловое ускорение a связано с линейным ускорение простым соотношением

(24)

и, используя уравнение (21), для него получим:

. (25)

Таким образом, измерив высоту и время падения гири, можно по формулам (23) и (25) вычислить вращающий момент и угловое ускорение для каждой серии опытов.

Используя разные гири и барабаны, можно изменять вращаю­щий момент. Момент инерции маятника – величина постоянная. Тормозящий момент от условий эксперимента зависит слабо, и его, в первом приближении, также можно считать постоянным. Это обстоятельство позволяет установить функциональную зависимость вращающего момента от углового ускорения маятника Обербека. Представим ее в виде линейной функции

. (26)

 

Константы, входящие в формулу (26), определим, воспользо­вавшись методом наименьших квадратов и экспериментальными данными:

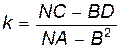, (27)

, (28)

где

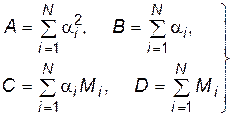, (29)

здесь a _i и – экспериментальные значения углового ускорения и вращающего момента, полученные в i -й серии опытов;

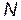– число серий опытов (в табл. 2а 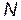=4).

Сравнивая уравнения (17) и (26), видим, что константа имеет смысл момента инерции, а константа – смысл тормозящего мо­мен­та. Поэтому можно положить, что

, (30)

. (31)

Близость величины к расчетному значению момента инерции подтверждает справедливость основного закона динамики вра­ща­тельного движения. Что же касается величины тормозящего мо­мен­та, то для обеспечения высокой точности результатов эксперимента должно выполняться неравенство 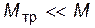. Соотношение этих двух величин позволяет, с одной стороны, ограничить снизу диапазон масс гирей, а, с другой стороны, оценить техническое состояние экспериментальной установки.

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: