 |
Постановка задачи обратного факторного анализа. Методы решения задачи.
|
|
|
|
Cпособ относительных разниц. Область применения
Для измерения влияния факторов на прирост результативного показателя используется способ относительных разностей. Этот метод применяется в мультипликативных моделях. Он значительно проще метода цепных подстановок, однако для его использования необходимо предварительно рассчитать относительные изменения всех показателей.
Методику расчета влияния факторов этим способом рассмотрим для мультипликативной модели типа у = ахbхc. При условии, что заданы конечные и начальные значения показателей, их относительные изменения определятся по формулам:
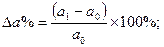
 и т.д.
и т.д.
Для расчета влияния первого фактора необходимо базисную (плановую) величину результативного показателя умножить на относительный прирост первого фактора, выраженного в процентах, и результат разделить на 100:

При определении влияния второго фактора необходимо к базисной величине результативного показателя прибавить его изменение за счет первого фактора, полученную сумму умножить на относительный прирост второго фактора в процентах и результат разделить на 100:

Влияние третьего фактора определяется следующим образом: к базисной величине результативного показателя необходимо прибавить его прирост за счет первого и второго факторов и полученную сумму умножить на относительный прирост третьего фактора и результат разделить на 100 и т. д.

Рассмотрим методику расчета способом относительных разниц на примере данных табл.4.3.
Таблица 4.3
Данные для факторного анализа
| Показатель | Начальный период | Конеч ный период | Отклоне- ние (+,-) | Темп роста, % |
| 1.Товарная продукция, тыс. грн. 2. Среднегодовая численность рабочих, чел. 3.Отработано всеми рабочими за период: -дней -часов 4.Средняя выработка одного рабочего за весь период, тыс грн. 5. Количество дней отработанных одним рабочим за период 6.Среднедневная выработка продукции одним рабочим, грн. 7.Средняя продолжительность рабочего дня 8.Среднечасовая выработка продукции одним рабочим, грн. | 166,67 651,04 7,6 85,663 | +60000 +200 +57200 +334720 +26,67 +6 +91,04 -0,4 +15,66 | 142,86 122,88 116,736 119,05 102,4 116,26 95,0 123,37 |
|
|
|
Изменение объема товарной продукции за счет:
· изменения численности рабочих —
∆ТП ЧР = ТП0 * ∆ЧР% /100 = 140000 *20% /100 = 28000 тыс.грн.;
· изменения количества дней, отработанных одним рабочим в анализируемом периоде, —
∆ТП КД = (ТП0 + ∆ТП чр)* ∆КД % /100 =(140000 +28000) * 2.4% /100 = 4032 тыс.грн.;
· изменения продолжительности рабочего дня —
∆ТП ПР = (ТП0 + ∆ТП ЧР + ∆ТП КД)* ∆ПР % /100 =(140000 +28000 + 4032)*(-0.5%)/ 100 = - 8600 тыс.грн.;
· изменения среднечасовой выработки одного рабочего —
∆ТП СЧВ = (ТП0 + ∆ТП ЧР + ∆ТП КД + ∆ТП ПР)* ∆СЧВ % /100 = =(140000 +28000 + 4032 –8600)* 23.37% /100 = 36568 тыс.грн.
Баланс отклонений: ∆ТП = ∆ТП ЧР + ∆ТП КД + ∆ТП ПР +∆ТП СЧВ
60000 =28000+4032-8600+36568.
Способ относительных разниц удобно применять в тех случаях, если требуется рассчитывать влияние большого комплекса факторов. В отличие от предыдущих способов здесь значительно сокращается число вычислительных процедур.
Область применения этого метода идентична области применения метода абсолютных разниц. Однако, когда исходные данные уже содержат рассчитанные ранее относительные изменения факторов в процентах или коэффициентах, метод относительных разниц проще метода цепной подстановки.
Логарифмический метод
Логарифмический метод состоит в том, что с его помощью достигается логарифмически пропорциональное распределение неразложимого остатка по факторам. При его использовании не требуется установления очерёдности действия факторов (как в методе цепных подстановок). Однако данный метод имеет и недостатки, главным среди них является то, что он не универсален, так как не может быть применен при анализе любого вида моделей факторных систем. Логарифмический метод применяется при решении задачи прямого детерминированного факторного анализа только с мультипликативными факторными системами.
|
|
|
Математически данный метод описывается следующим образом. Факторную систему z = ab можно представить в виде lgz = lga + lgb,
тогда Δz = lgz1 – lgz0 = (lga1 – lga0) + (lgb1 – lgb0) или
lg(z1 : z0) = lg(a1 :a0) + lg(b1 : b0).
Разделив обе части формулы на lg(z1 : z0) и умножив на Δz, получим:

| (4.18) |
или
Δz = Δza + Δzb = k lg(a1 : a0) + k lg(b1 : b0),
где

|
Выражение (4.18) представляет собой для Δz не что иное, как его логарифмическое пропорциональное распределение по двум искомым факторам. Особенность логарифмического метода разложения состоит в том, что он позволяет определить безостаточное влияние не только двух, но и многих изолированных факторов на изменение результативного показателя, не требуя установления очерёдности действия.
Рассмотрим применение логарифмического метода, использовав данные табл. 4.8. Требуется определить влияние факторов первого порядка на изменение фондоотдачи основных средств предприятия. Факторная модель результативного показателя имеет вид:
ФО = У х ФОМ.
Таблица 4.8
Исходные данные для факторного анализа
| Показатель | Базисный период | Отчетный период | Индекс |
| Фондоотдача основных фондов, коэф. (ФО) | 7,55 | 7,2 | 0.9536423 |
| Удельный вес стоимости машин и оборудования в общей стоимости основных средств, коэф. (У) | 0,604 | 0,6 | 0.9933774 |
| Фондоотдача машин и оборудования,коэф. (ФОМ) | 12,55 | 12,0 | 0,96 |
Фондоотдача основных средств предприятия уменьшилась на 0,046 пункта (0.9536423 – 1.0), в том числе за счет изменения:
· удельного веса машин и оборудования в составе основных средств предприятия
∆ФОУ = ∆ФО(lgIУ : lgIФО) = - 035 (lg 0.9933774: lg 0.9536423) = -005;
· фондоотдачи активной части основных средств:
|
|
|
∆ФОФОМ = ∆ФО(lgIФОМ : lgIФО) = - 035 (lg 0,96: lg 0.9536423) = –0,3;
· баланс отклонений: –0,35.
Таким образом, уменьшение фондоотдачи основных средств происходило за счет уменьшения значения двух факторов.
Индексный метод
Индекс представляет собой относительную величину, полученную в результате сопоставления уровней сложных социально-экономических показателей во времени.
С помощью индексного метода решаются следующие основные задачи:
- характеризуется общее изменение сложных экономических показателей (например, затрат на производство продукции, стоимости произведенной продукции, и т. д.) или формирующих их показателей-факторов;
- определяется влияние одного из факторов на изменение сложного экономического показателя путем элиминирования влияния других факторов (например, влияние изменения цен на продукцию на изменение выручки от реализации продукции);
- обосновывается влияние изменения структуры показателя на индексируемую величину (например, при изучении динамики среднеотраслевой себестоимости продукции исследуется влияние изменения в распределении объёма выпуска продукции по предприятиям отрасли).
В развитии индексной теории сложились два направления:
- обобщающее, или синтетическое, которое трактует индекс как показатель среднего изменения уровня анализируемой величины;
- аналитическое, в котором индексы – это показатели изменения уровня результативного показателя под влиянием изменения индексируемой величины.
В зависимости от содержания и характера индексируемой величины различают индексы количественных (объёмных) показателей (например, индекс физического объёма продукции) и индексы качественных показателей (например, индекс себестоимости и др.).
Как было отмечено выше, индексы могут также применяться в аналитических целях для оценки влияния на результативный показатель изменения факторов, его формирующих. Предпосылкой для проведения анализа в индексной форме является возможность представления результативного экономического показателя в виде суммы произведений его факторов. Например, стоимостной объём экспорта может быть представлен произведением уровня внешнеторговых цен pi на объём экспортных поставок в натуральном выражении qi. Таким образом, стоимость экспорта (результативный показатель) будет зависеть от изменения внешнеторговых цен и объёма поставок продукции в натуральном выражении.
|
|
|
Оценить роль факторов в изменении результативного показателя можно путем построения системы взаимосвязанных индексов. Задача состоит в том, чтобы рассчитать изменение сложного показателя при изменении величины только одного фактора так, чтобы величина других факторов была бы сохранена на определённом постоянном уровне. Таким образом, в основе приёма построения аналитических индексов лежит принцип элиминирования (изменение величины всех факторов, кроме изучаемого).
Сформулируем правила построения аналитических(факторных) индексов:
при расчете аналитических (факторных) индексов количественных показателей соизмерители принимаются на уровне базисного периода;
при расчете аналитических (факторных) индексов качественных показателей соизмерители принимаются на уровне текущего периода.
Например, для того чтобы определить изменение стоимости продукции предприятия в связи с изменением физического объема продукции и цен на нее, достаточно представить взаимосвязь индексов вышеперечисленных показателей и рассчитать значения индексов:
Iqp = Iq x Ip.
Для того чтобы динамика цен не повлияла на исследуемый показатель, при расчете индекса физического объёма, цены принимаются за базисный период, тогда индекс физического объёма можно записать в виде:
 . .
| (4.7) |
Однако при этом для того, чтобы изменение уровней объёма производства в отчётном и базисном периодах не повлияло на уровень цен, принято в качестве соизмерителя вводить объём продукции отчётного периода ( ), тогда общий индекс цен можно выразить:
), тогда общий индекс цен можно выразить:

| (4.7) |
Корректность определения размера каждого фактора зависит от:
1) количества знаков после запятой (не менее четырех);
2) количества самих факторов (связь обратно пропорциональна).
Принципы построения индексов: изменение одного фактора при неизменном значении всех остальных, при этом если обобщающий экономический показатель представляет собой произведение количественного (объемного) и качественного показателей-факторов, то при определении влияния количественного фактора качественный показатель фиксируется на базисном уровне, а при определении влияния качественного фактора количественный показатель фиксируется на уровне отчетного периода.
|
|
|
Пусть Y = а⋅Ь⋅с⋅d. Тогда:

При этом: lY =la⋅lb⋅lc⋅ld.
Индексный метод позволяет провести разложение по факторам не только относительных, но и абсолютных отклонений обобщающего показателя. В этом случае влияние отдельных факторов определяется с помощью разности между числителем и знаменателем соответствующих индексов, т. е. также при расчете влияния одного фактора элиминируется влияние другого:
Пусть Y = а⋅Ь, где а – количественный фактор, ab – качественный. Тогда:
a1⋅b0 —a0⋅b0 – абсолютный прирост результирующего показателя за счет фактора а;
a1⋅b1 —a1⋅b0 – абсолютный прирост результирующего показателя за счет фактора b;
a1⋅b1 —a0⋅b0 – абсолютный прирост результирующего показателя за счет влияния всех факторов.
Данный принцип разложения абсолютного прироста (отклонения) обобщающего показателя по факторам пригоден для случая, когда число факторов равно двум (один из них количественный, другой – качественный), а анализируемый показатель представлен как их произведение.
Постановка задачи обратного факторного анализа. Методы решения задачи.
Обратный факторный анализ осуществляет исследование причинно-следственных связей способом логической индукции — от частных, отдельных факторов к обобщающим, от причин к следствиям с целью установления чувствительности изменения многих результативных показателей к изменению изучаемого фактора.
Пусть имеется набор показателей х,, х,.... х„, характеризующих некоторый экономический процесс (L). Каждый из показателей односторонне характеризует процесс L. Требуется построить функцию f(xJ изменения процесса L, содержащую в себе основные характеристики всех показателей, х, х„ или некоторых из них в комплексе. В зависимости от цели исследования функция) должна характеризовать процесс в статике или в динамике. Данная постановка задачи называется задачей обратного факторного анализа.
Задачи обратного, факторного анализа могут быть детерминированными и стохастическими. Примерами задачи обратного детерминированного факторного анализа являются задачи комплексной оценки производственнохозяйственной деятельности, а также задачи математического программирования, в том числе и линейного. Примером задачи обратного стохастического факторного анализа могут служить производственные функции, которыми устанавливаются зависимости между величиной выпуска продукции и затратами производственных факторов (первичных ресурсов).
К методам сравнительной комплексной оценки относятся следующие: суммирование значений всех показателей, суммы мест, суммы баллов, расстояний, таксонометрический.
Исходной информацией при использовании всех перечисленных выше методов служит матрица, элементами которой являются значения показателей.
Метод расстояний
Основой метода расстояний является учет близости объектов по сравнению с показателями объекта = эталона.
В данном методе помимо информации о показателях (X), коэффициентах сравнительной значимости показателей (k j) и характеристик направленности действия показателей (Sj) требуется определить подразделение=эталон. Это реально не существующее подразделение характеризуется лучшими значениями по каждому оценочному показателю. Показатели подразделения эталона x0 j строятся следующим образом:
xoj = max xij при Sj =+1;
xoj = min xij при Sj = -1.
В некоторых случаях за объект-эталон принимается объект, значения показателей которого равны средним арифметическим уровням показателей в изучаемой совокупности. Однако в совокупности экономических объектов, где преобладают асимметричные распределения, среднее арифметическое в качестве характеристики типичного, эталонного объекта утрачивает своё значение.
Ряд экономистов предлагает использовать в качестве эталона 100%-ное выполнение плана по всем оценочным показателям, указывается при этом на нежелательность как недовыполнения, так и перевыполнения плана.
В тех случаях, когда элементами расстояний являются несоизмеримые величины показателей, проводится нормирование путём деления значений показателей xij на значение показателя эталонного объекта xoj. Оценка Ri каждого i -го подразделения определяется как квадрат расстояния между двумя точками в m -мерном пространстве. Координаты первой – это значения показателей подразделения эталона, а координаты второй – показатели подразделений i. Коэффициент комплексной сравнительной оценки определяется по формуле:
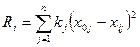 
| (6.8) |
Для вычисления «действительного» расстояния между точками m – мерного пространства необходимо извлечь квадратный корень из всех величин Ri. Коэффициенты сравнительной значимости kj необходимы для придания веса различным показателям в соответствии с их важностью. Чем больше kj, тем более значимпоказатель j, тем вбольшей степени отклонение от эталона будет влиять на общую суммарную оценку.
Критерий оценки лучшего подразделения: min Ri (1 < i < m).
Метод расстояний наиболее формализован по сравнению с другими методами. Вместе с этим и он имеет ряд недостатков. Во-первых, сама по себе процедура оценки нуждается в совершенствовании: вариации различных показателей могут отличаться друг от друга, а это значит, что показатели с большей вариацией будут иметь больший удельный вес в суммарной оценке, и, следовательно, они получают преимущество по сравнению с другими показателями; во-вторых, процедура вычислений достаточно сложна, а результаты не столь наглядны.
|
|
|


