 |
Энтропия источника дискретных сообщений (ИДС) и её свойства
|
|
|
|
Балтийский федеральный университет имени И. Канта
Физико-технический факультет
| Утверждаю |
| Заведующий кафедры |
| к.т.н., доцент |
| А. Шпилевой |
| «___»_________ 201__ г. |
Л Е К Ц И Я № 29
Тема: «Основные понятия теории информации»
Текст лекции по дисциплине: «Теория электрической связи»
| Обсуждена и одобрена на заседании кафедры |
| протокол №___ от «___»___________201__г. |
Г. Калининград 2012 г.
Текст лекции № 30
по дисциплине: «Теория электрической связи»
«Основные понятия теории информации»
Введение
В каналах связи передаётся информация, преобразованная в сигналы.
Для согласования объёма информации с каналом необходимо научиться определять количество информации, подлежащее передаче. Без решения этого вопроса невозможно строить современные системы передачи информации.
Под термином “информация” понимают различные сведения, которые поступают к получателю. В более строгой форме определение информации следующее:
Информация – это сведения, являющиеся объектом передачи, распределения, преобразования, хранения или непосредственного использования.
В дальнейшем нас будут интересовать лишь вопросы, связанные с информацией как объектом передачи.
Сообщение является формой представления информации.
Одно и то же сведение может быть представлено в различной форме. Например, передача голосового сообщения по телефону или изображения по телевизионному каналу. В этом случае мы имеем дело с информацией, представленной в непрерывном виде (непрерывное сообщение). Будем считать, что это сообщение вырабатывается источником непрерывных сообщений. Либо мы передаем сообщение по телеграфному каналу, в этом случае речь идет об информации, представленной в дискретном виде (дискретное сообщение). Это сообщение вырабатывается источником дискретных сообщений.
|
|
|
В технических устройствах и системах прием, обработка и передача информации осуществляется с помощью сигналов.
Сигнал (от латинского signum – знак) представляет собой любой процесс, несущий информацию.
Сигналы отражают физические характеристики изучаемых объектов и процессов. Посредством сигналов информация может передаваться на короткие и большие расстояния. Информация в виде сигнала может различным образом перерабатываться, сохраняться, уничтожаться и т. п.
Различают несколько видов сигналов: звуковые, которые можно услышать при работе милицейской сирены; световые, передающие информацию от пульта дистанционного управления к телевизору, а также электрические.
Основное отличие дискретного и непрерывного источников состоит в следующем. Множество всех различных сообщений, вырабатываемых дискретным источником всегда конечно. Поэтому на конечном отрезке времени количество символов дискретного источника так же является конечным. В то же время число возможных различных значений звукового давления (или напряжения в телефонной линии), измеренное при разговоре, даже на конечном отрезке времени, будет бесконечным.
В нашем курсе мы будем рассматривать вопросы передачи именно дискретных сообщений.
Информация, содержащаяся в сообщении, передается от источника сообщений к получателю по каналу передачи дискретных сообщений (ПДС).

|
| Рис.1. Тракт передачи дискретных сообщений |
Вид передаваемого сигнала определяет тип канала связи.
Понятие информации, постановка задачи её определения.
Какое количество информации содержится, к примеру, в тексте романа «Война и мир», во фресках Рафаэля или в генетическом коде человека? Возможно ли, объективно измерить количество информации?
|
|
|
Определить понятие «количество информации» довольно сложно. В решении этой проблемы существуют два основных подхода. Исторически они возникли почти одновременно. В конце 40-х годов XX века один из основоположников кибернетики американский математик Клод Шеннон развил вероятностный подход к измерению количества информации, а работы по созданию ЭВМ привели к «объемному» подходу.
Вероятностный подход
Этот подход заключается в том, что понятие «количество информации», основывается на том, что информацию, содержащуюся в сообщении, можно нестрого трактовать в смысле ее новизны или, иначе, уменьшения неопределенности наших знаний об объекте.
При этом понятие «информация» связывается с вероятностью осуществления того или иного события.
Американский инженер Р. Хартли (1928 г.) процесс получения информации рассматривал как выбор одного сообщения из конечного заранее заданного множества из  равновероятных сообщений, а количество информации
равновероятных сообщений, а количество информации 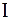 , содержащееся в выбранном сообщении, определял как двоичный логарифм
, содержащееся в выбранном сообщении, определял как двоичный логарифм  .
.
Формула Хартли:
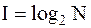 ; ;
| (1.1) | |||
| где | 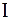
| – | количество информации | |

| – | число возможных состояний | ||
Ту же формулу можно представить иначе:
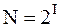 ; ;
| (1.2) |
Допустим, нужно угадать одно число из набора натуральных целых чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: 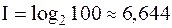 . То есть сообщение о верно угаданном числе содержит количество информации, приблизительно равное
. То есть сообщение о верно угаданном числе содержит количество информации, приблизительно равное 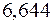 .
.
Приведем примеры равновероятных сообщений: при бросании монеты: «выпала решка», «выпал орел»; на странице книги: «количество букв четное», «количество букв нечетное».
Определим теперь, являются ли равновероятными сообщения «первой выйдет из дверей здания женщина» и «первым выйдет из дверей здания мужчина». Однозначно ответить на этот вопрос нельзя. Все зависит от того, о каком именно здании идет речь. Если это, например, станция метро, то вероятность выйти из дверей первым одинакова для мужчины и женщины, а если это военная казарма, то для мужчины эта вероятность значительно выше, чем для женщины.
|
|
|
Для задач такого рода американский ученый Клод Шеннон предложил в 1948г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе.
Формула Шеннона:
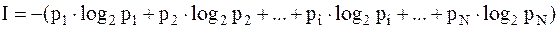 ; ;
| (1.3) | |||
| где | 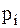
| – | вероятность того, что именно  -e сообщение выделено в наборе из -e сообщение выделено в наборе из  сообщений сообщений
| |
Если вероятности  равны, то каждая из них равна
равны, то каждая из них равна 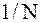 , и формула Шеннона превращается в формулу Хартли.
, и формула Шеннона превращается в формулу Хартли.
Анализ формулы показывает, что чем выше вероятность события, тем меньшее количество информации возникает после его осуществления, и наоборот.
Если вероятность равна 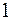 (т.е. событие достоверно), количество информации равно
(т.е. событие достоверно), количество информации равно  . Если вероятность свершения или не свершения, какого либо события одинакова, т.е. равна
. Если вероятность свершения или не свершения, какого либо события одинакова, т.е. равна 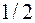 , то количество информации, которое несет с собой это событие, равно
, то количество информации, которое несет с собой это событие, равно 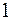 .
.
Это – единица измерения информации. Она получила наименование бит.
Если событие имеет 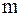 равновероятных исходов, как при подбрасывании монеты или при игре в кости, то вероятность конкретного исхода равна
равновероятных исходов, как при подбрасывании монеты или при игре в кости, то вероятность конкретного исхода равна 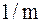 , и формула Шеннона приобретает вид:
, и формула Шеннона приобретает вид: 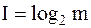 .
.
В качестве примера определим количество информации, связанное с появлением каждого символа в сообщениях, записанных на русском языке. Будем считать, что русский алфавит состоит из 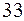 букв и знака «пробел» для разделения слов. По формуле Хартли:
букв и знака «пробел» для разделения слов. По формуле Хартли:
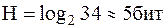 ; ;
| (1.4) |
Однако, в словах русского языка (равно как и в словах других языков) различные буквы встречаются неодинаково часто. Ниже приведена таблица 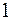 вероятностей частоты употребления различных знаков русского алфавита, полученная на основе анализа очень больших по объему текстов.
вероятностей частоты употребления различных знаков русского алфавита, полученная на основе анализа очень больших по объему текстов.
Воспользуемся для подсчета 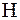 формулой Шеннона;
формулой Шеннона; 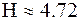 бит. Полученное значение
бит. Полученное значение 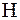 , как и можно было предположить, меньше вычисленного ранее. Величина
, как и можно было предположить, меньше вычисленного ранее. Величина 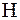 ,вычисляемая по формуле Хартли, является максимальным количеством информации, которое могло бы приходиться на один знак.
,вычисляемая по формуле Хартли, является максимальным количеством информации, которое могло бы приходиться на один знак.
Таблица  . Частотность букв русского языка
. Частотность букв русского языка
| i | Символ | P(i) | i | Символ | P(i) | i | Символ | P(i) |
| Пробел | 0,175 | К | 0,028 | Г | 0.012 | |||
| 0,090 | М | 0,026 | Ч | 0,012 | ||||
| Е | 0,072 | Д | 0,025 | И | 0,010 | |||
| Ё | 0,072 | П | 0,023 | X | 0,009 | |||
| А | 0,062 | У | 0,021 | Ж | 0,007 | |||
| И | 0,062 | Я | 0,018 | Ю | 0,006 | |||
| Т | 0,053 | Ы | 0,016 | Ш | 0.006 | |||
| Н | 0,053 | З | 0.016 | Ц | 0,004 | |||
| С | 0,045 | Ь | 0,014 | Щ | 0,003 | |||
| Р | 0,040 | Ъ | 0,014 | Э | 0,003 | |||
| В | 0,038 | Б | 0,014 | Ф | 0,002 | |||
| Л | 0,035 |
|
|
|
Запомните комбинацию из 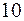 наиболее повторяющихся букв русского алфавита СЕНОВАЛИТР. Эти знания использовали дешифровальщики при вскрытии тайных переписок в различные исторические периоды.
наиболее повторяющихся букв русского алфавита СЕНОВАЛИТР. Эти знания использовали дешифровальщики при вскрытии тайных переписок в различные исторические периоды.
Аналогичные подсчеты 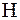 можно провести и для других языков, например, использующих латинский алфавит – английского, немецкого, французского и др. (
можно провести и для других языков, например, использующих латинский алфавит – английского, немецкого, французского и др. ( различных букв и «пробел»).
различных букв и «пробел»).
Рассмотрим алфавит, состоящий из двух знаков  и
и 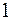 . Если считать, что со знаками
. Если считать, что со знаками  и
и 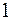 в двоичном алфавите связаны одинаковые вероятности их появления
в двоичном алфавите связаны одинаковые вероятности их появления  , то количество информации на один знак при двоичном кодировании будет равно:
, то количество информации на один знак при двоичном кодировании будет равно:
 ; ;
| (1.5) |
Таким образом бит можно также определить как количество информации, которое содержит один разряд двоичного числа (отсюда название «бит»: b inary dig it — двоичный разряд). Другими словами количество информации (в битах), заключенное в двоичном слове, равно числу двоичных знаков в нем.
Один бит -это количество информации, которое переносит один символ источника дискретных сообщений в том случае, когда алфавит источника состоит из двух равновероятных символов.
Количество информации, равное 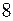 битам, называется байтом.
битам, называется байтом.
В восьми разрядах можно записать 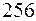 различных целых двоичных чисел от
различных целых двоичных чисел от 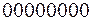 до
до  . Этого вполне достаточно для представления в двоичной форме информации об алфавитах Русском и Латинском, всех знаках препинания, цифрах от
. Этого вполне достаточно для представления в двоичной форме информации об алфавитах Русском и Латинском, всех знаках препинания, цифрах от  до
до 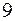 , арифметических и алгебраических действиях, а так же специальных символов (например § @ $).
, арифметических и алгебраических действиях, а так же специальных символов (например § @ $).
Отметим, что создатели компьютеров отдают предпочтение именно двоичной системе счисления потому, что в техническом устройстве наиболее просто реализовать два противоположных физических состояния: некоторый физический элемент, имеющий два различных состояния: намагниченность в двух противоположных направлениях; прибор, пропускающий или нет электрический ток; конденсатор, заряженный или незаряженный и т.п.
Выводы
1. Единицей количества информации является 1 бит.
2. Для определения частного количества информации используется логарифмическая величина.
Энтропия источника дискретных сообщений (ИДС) и её свойства
Энтропия 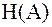 – среднее количество информации, которое приходится на одно сообщение (один символ последовательности), поступающее от источника без памяти. Получим, применяя операцию усреднения по всему объему алфавита
– среднее количество информации, которое приходится на одно сообщение (один символ последовательности), поступающее от источника без памяти. Получим, применяя операцию усреднения по всему объему алфавита
|
|
|
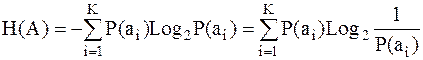 ;[бит/символ] ;[бит/символ]
| (2.1) |
Выражение (2.1) известно как формула Шеннона для энтропии источника дискретных сообщений. Энтропия – мера неопределенности в поведении источника дискретных сообщений.
Энтропия равна нулю, если с вероятностью единица источником выдается всегда одно и то же сообщение (в этом случае неопределенность в поведении источника сообщений отсутствует). Энтропия максимальна, если символы источника появляются независимо и с одинаковой вероятностью.
Свойства энтропии:
1. Энтропия любого источника сообщений всегда положительна, 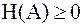 . Энтропия равна нулю,
. Энтропия равна нулю, 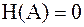 , если источник выдаёт одно и тоже сообщение с вероятностью, равной
, если источник выдаёт одно и тоже сообщение с вероятностью, равной  .
.
2. Если источник без памяти содержит сообщения с фиксированным объёмом алфавита K, то энтропия такого источника имеет максимальное значение при условии равновероятной выдачи сообщений.
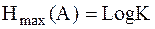 , при
, при 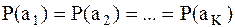 .
.
В частном случае, когда источник выдаёт всего два сообщения 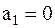 и
и 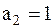 , энтропия максимальна и равна
, энтропия максимальна и равна 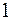 биту при
биту при  . Покажем это.
. Покажем это.
Введём обозначения: 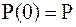 ,
,  , тогда
, тогда
 ; ;
| (2.2) |
Отсюда видно, что 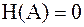 при
при  и
и  или
или 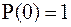 и
и  . Максимум энтропии достигается, если
. Максимум энтропии достигается, если  , т. е.
, т. е.
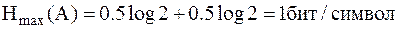 ; ;
| (2.3) |
 Зависимость энтропии этого источника от
Зависимость энтропии этого источника от 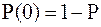 (1) показана на рисунке 2.
(1) показана на рисунке 2.

|
| Рис. 2. Энтропия двоичного источника без памяти |
3. Энтропия аддитивна. Это вытекает из свойств логарифмической функции.
Аддитивность (лат. additivus — прибавляемый) — свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям, в некотором классе возможных разбиений объекта на части. Например, аддитивность объёма означает, что объём целого тела равен сумме объёмов составляющих его частей.
Выводы
1. Среднее количество информации, содержащееся в одном символе источника, оценивается энтропией.
|
|
|


