Динамика механических колебаний

Механические колебания и волны

1. Кинематика гармонических колебаний.

2. Динамика механических колебаний.

3. Маятники.

4. Волны в упругих средах.

5. Звук.

Кинематика гармонических колебаний

Колебаниями называются процессы, в той или иной степени, повторяющиеся во времени.

Так движение точки по окружности является периодическим процессом, значит условно, может рассматриваться моделью колебательных движений. Действительно, пусть материальная точка C движется с постоянной угловой скоростью ω по окружности радиуса A (рис.1). При этом угловая координата точки будет изменяться по закону

, (1)

где φ ₀ - начальная координата точки.

Не смотря на то, что угол поворота монотонно возрастает, через равные промежутки времени, равные периоду вращения

точка возвращается в исходное положение, в котором ее кинематические характеристики (скорость, ускорение) принимают исходные значения.

Поэтому движение проекции точки на любую из осей координат является колебательным движением вдоль прямой.

Угол поворота при колебании изменяется в соответствии с формулой (1), из него можно получить закон изменения координаты точки от времени

X(t) = A cos(w t+ ). (2)

Движение, при котором координата точки изменяется по закону косинуса (или синуса) называется гармоническим колебанием.

Таким образом, при равномерном движении точки по окружности ее проекция совершает гармонические колебания.

Как следует из вида функции (2), гармоническое колебание точки определяется тремя параметрами.

Параметр A называется амплитудой колебаний, он равен максимальному отклонению точки от центрального (равновестного) положения. Эта величина имеет ту же размерность, что и координата x, то есть размерность длины.

Изменяющаяся величина называется фазой колебания, а величина φ ₀ - начальной фазой.

Параметр ω называется круговой частотой колебаний.

Круговая частота связана с периодом колебания соотношением (3)

Обычная частота ν - число колебаний в единицу времени.

Если период – это время одного колебания, то величина обратная периоду равна числу колебаний в единицу времени, то есть частоте колебаний . (4)

С помощью соотношений (3) и (4) легко связать круговую и обычную частоты колебаний 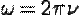. (5)

Так скорость это первая производная от координаты, то для колебаний имеем

(6)

Величина V₀= wA равна максимальной скорости движения точки при гармонических колебаниях.

Аналогичным образом можно найти ускорение точки, совершающей гармонические колебания.

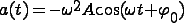. (7)

Между ускорением точки и ее координатой как видно из уравнений (7) и (2) существует взаимосвязь

. (8)

При гармонических колебаниях ускорение точки пропорционально его координате, с отрицательным коэффициентом пропорциональности.

Динамика механических колебаний

По второму закону Ньютона сила, действующая на материальную точку массой m с учетом (8):

F = ma = – m w₀²x. (9)

Отсюда:

1) модуль силы пропорционален смещению материальной точки из положения равновесия;

2) направление силы и смещения противоположны.

Следовательно, сила всегда направлена к положению равновесия. Такие силы называются возвращающими. Зависимость (9) характерна для упругой силы.

Найдем энергию свободных колебаний под действием упругих сил. Она представлена двумя видами энергии: кинетической и потенциальной.

Подставляя в эту формулу значения х и v согласно соотношениям (2) и (6), получим:

Таким образом, энергия свободных колебаний пропорциональна квадрату амплитуды колебаний.

Вследствие сопротивления свободные колебания всегда рано или поздно затухают.

Обычно затухание колебаний характеризуется декрементом затухания, он показывает, во сколько раз уменьшается амплитуда колебаний за время, равное периоду колебаний.

Маятники

Маятник - тело, совершающее под действием переменной силы колебания.

1. Пружинный маятник — это груз массой m, который подвешен на пружине и совершает гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины.

Пружинный маятник совершает гармонические колебания по закону

х = А соs (ω₀t+φ)

с циклической частотой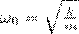

и периодом 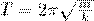(15)

Формула (15) верна для упругих колебаний в границах, в которых выполняется закон Гука.

2. Физический маятник — это твердое тело, которое совершает колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, которая проходит через точку О, не совпадающую с центром масс С тела.

3. Математический маятник — это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести.

Хорошее приближение математического маятника есть небольшой тяжелый шарик, который подвешен на длинной тонкой нити.

Периода малых колебаний математического маятника

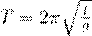
Волны в упругих средах

Если в каком-либо месте упругой (твердой, жидкой или газообразной) среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание будет распространяться в среде от частицы к частице с некоторой скоростью v. Процесс распространения колебаний в пространстве называется волной.

В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны.

В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны.

В жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных волн.

Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью.

Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы

Расстояние λ, на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны

= vТ,

где v– скорость волны, Т – период колебаний.

Звук

Поделиться:

Воспользуйтесь поиском по сайту: