 |
Потери напора при турбулентном равномерном движении жидкости.
|
|
|
|
Распределение скоростей по живому сечению в цилиндрической трубе при ламинарном режиме.

Если боковая поверхность трубы есть поверхность цилиндра, то естественно допустить существование ламинарного течения с линиями тока в виде прямых, параллельных образующим цилиндра.
Для отыскания скорости имеем уравнение Пуассона с постоянной правой частью
 (1.67)
(1.67)
граничным условием которого является равенство нулю скорости не стенке трубы.
В общем случае рассматриваемое течение может быть обусловлено как перепадом давления  , так и осевым движением одного из цилиндров (речь идёт о рассмотрении цилиндрической трубы, состоящей из двух цилиндров (рис. 1.20)).
, так и осевым движением одного из цилиндров (речь идёт о рассмотрении цилиндрической трубы, состоящей из двух цилиндров (рис. 1.20)).
Допустим, что внутренний цилиндр перемещается в направлении оси z со скоростью  . Такому движению соответствуют граничные условия
. Такому движению соответствуют граничные условия 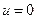 при
при 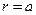 ,
, 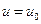 при
при 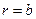 . Использовав их для определения постоянных
. Использовав их для определения постоянных 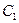 и
и  , найдём
, найдём
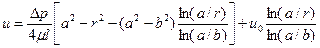 (1.68)
(1.68)
В частном случае, если перепада давления нет, то получим осесиммитричное течение Куэтта с распределением скоростей

и касательными напряжениями в слое жидкости
 ,
,
где  .
.
Из этой формулы следует, что если зазор между цилиндрами 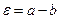 мал, то касательные напряжения в слое жидкости могут быть весьма значительными.
мал, то касательные напряжения в слое жидкости могут быть весьма значительными.
При неподвижных цилиндрах ( ) имеем течение в кольцевой трубе с распределением скоростей
) имеем течение в кольцевой трубе с распределением скоростей
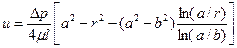 (1.69)
(1.69)
Эта зависимость позволяет вычислить все другие характеристики течения. В частности, расход
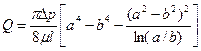 (1.70)
(1.70)
Разделив расход на площадь  кольца, найдём выражение для средней скорости
кольца, найдём выражение для средней скорости
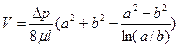 , (1.71)
, (1.71)
которое позволяет вычислять падение давления в кольцевой трубе.
Коэффициент Дарси при ламинарном движении.
Во многих случаях приближённо можно считать, что потери энергии при протекании жидкости[3] через элемент гидравлической системы пропорциональны квадрату скорости жидкости. По этой причине удобно бывает характеризовать сопротивление безразмерной величиной ζ, которая называется коэффициент потерь или коэффициент местного сопротивления и такова, что
|
|
|
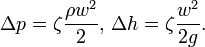
То есть в предположении, что скорость w по всему сечению потока одинакова, ζ=Δ p / e торм, где e торм = ρ w ²/2 — энергия торможения единицы объёма потока относительно канала. Реально в потоке скорость жидкости не равномерна, в справочной литературе в данных формулах принимается среднерасходная скорость w = Q / F, где Q — объёмный расход, F — площадь сечения, для которого рассчитывается скорость. Таким образом, средняя энергия торможения потока обычно несколько больше ρ w ²/2, см. Среднее квадратическое.
Для линейных потерь обычно пользуются коэффициентом потерь на трение по длине (также коэффициент Дарси) λ, фигурирующего в формуле Дарси — Вейсбаха[2]
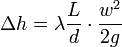 ,
,
где L - длина элемента, d - характерный размер сечения (для круглых труб это диаметр). Иначе в единицах давления
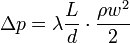 ;
;
таким образом, для линейного элемента относительной длины L / d коэффициент сопротивления трения ζтр=λ L / d.
Потери напора при турбулентном равномерном движении жидкости.
| Потери напора на трение | |||||||||
При равномерном движении жидкости в трубах потери давления на трение как при ламинарном, так и при турбулентном режимах движения рассчитывают по формуле Дарси–Вейсбаха:
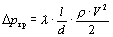 ,
где l – коэффициент гидравлического трения; l – длина трубопровода; d – его диаметр; r – плотность жидкости; V – средняя скорость ее течения.
Коэффициент гидравлического трения зависит от режима движения жидкости, значения критерия Рейнольдса: ,
где l – коэффициент гидравлического трения; l – длина трубопровода; d – его диаметр; r – плотность жидкости; V – средняя скорость ее течения.
Коэффициент гидравлического трения зависит от режима движения жидкости, значения критерия Рейнольдса:
 и состояния стенок трубы, которое характеризуется относительной шероховатостью:
и состояния стенок трубы, которое характеризуется относительной шероховатостью:
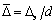 ,
где Dэ – эквивалентная равномерно-зернистая шероховатость (см. табл. П 1.7) (т.е. такая высота неровностей, образованных песчинками одинакового размера, которая при расчете дает одинаковое с действительной шероховатостью значение коэффициента гидравлического трения).
При ламинарном режиме течения коэффициент гидравлического трения рассчитывают по формуле ,
где Dэ – эквивалентная равномерно-зернистая шероховатость (см. табл. П 1.7) (т.е. такая высота неровностей, образованных песчинками одинакового размера, которая при расчете дает одинаковое с действительной шероховатостью значение коэффициента гидравлического трения).
При ламинарном режиме течения коэффициент гидравлического трения рассчитывают по формуле
 .
При турбулентном режиме течения весь диапазон значений чисел Рейнольдса, в зависимости от относительной шероховатости, разбивают на области, каждой из которых соответствует своя формула для расчета коэффициента гидравлического трения:
область гидравлически гладких труб .
При турбулентном режиме течения весь диапазон значений чисел Рейнольдса, в зависимости от относительной шероховатости, разбивают на области, каждой из которых соответствует своя формула для расчета коэффициента гидравлического трения:
область гидравлически гладких труб 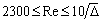 : :
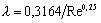 – формула Блазиуса;
переходная область – формула Блазиуса;
переходная область  : :
 – формула А.Д. Альтшуля;
квадратичная область – формула А.Д. Альтшуля;
квадратичная область  : :
 – формула Б.Л. Шифринсона.
В случае течения жидкости по трубам, форма поперечного сечения которых отличается от круга, в приведенных выше формулах используют вместо d эквивалентный диаметр: – формула Б.Л. Шифринсона.
В случае течения жидкости по трубам, форма поперечного сечения которых отличается от круга, в приведенных выше формулах используют вместо d эквивалентный диаметр:
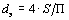 ,
где S – площадь поперечного сечения трубы; П – полный смоченный периметр трубы.
Коэффициент гидравлического трения при ламинарном течении в трубах различной формы рассчитывают по формуле ,
где S – площадь поперечного сечения трубы; П – полный смоченный периметр трубы.
Коэффициент гидравлического трения при ламинарном течении в трубах различной формы рассчитывают по формуле
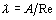 ,
где А – коэффициент, численное значение которого зависит от формы поперечного сечения трубы (см. табл. П 1.8).
Пропускная способность трубопроводов в период эксплуатации снижается. Вследствие коррозии и образования отложений в трубах шероховатость их увеличивается, что в первом приближении можно оценить по формуле ,
где А – коэффициент, численное значение которого зависит от формы поперечного сечения трубы (см. табл. П 1.8).
Пропускная способность трубопроводов в период эксплуатации снижается. Вследствие коррозии и образования отложений в трубах шероховатость их увеличивается, что в первом приближении можно оценить по формуле
 ,
где Dо – абсолютная шероховатость новых труб, мм; D t – абсолютная шероховатость через t лет эксплуатации, мм; a – коэффициент, характеризующий быстроту возрастания шероховатости, мм/год.
Сифоном называют соединяющий два резервуара трубопровод, часть которого расположена выше уровня жидкости в напорном резервуаре. Допускаемое возвышение верхней точки сифона определяют по формуле ,
где Dо – абсолютная шероховатость новых труб, мм; D t – абсолютная шероховатость через t лет эксплуатации, мм; a – коэффициент, характеризующий быстроту возрастания шероховатости, мм/год.
Сифоном называют соединяющий два резервуара трубопровод, часть которого расположена выше уровня жидкости в напорном резервуаре. Допускаемое возвышение верхней точки сифона определяют по формуле
 ,
где ,
где  – потеря давления на участке от напорного резервуара до верхней точки сифона. Минимально допускаемое давление в верхней точке сифона должно быть выше давления насыщения при данной температуре. – потеря давления на участке от напорного резервуара до верхней точки сифона. Минимально допускаемое давление в верхней точке сифона должно быть выше давления насыщения при данной температуре.
| |||||||||
| Местные потери давления в трубах | |||||||||
Местные сопротивления, к которым относят арматуру, фасонные части трубопроводов и прочее оборудование, вызывают изменения величины и (или) направления скорости движения жидкости на отдельных участках трубопроводов, что приводит к потерям давления в них. Потери давления определяют по формуле Вейсбаха:
 .
Значения коэффициентов местных сопротивлений V зависят от конфигурации местного сопротивления и режима течения жидкости перед ним.
При внезапном сужении трубопровода (резком изменении площади проходного сечения от S 1 до S 2) коэффициент местного сопротивления .
Значения коэффициентов местных сопротивлений V зависят от конфигурации местного сопротивления и режима течения жидкости перед ним.
При внезапном сужении трубопровода (резком изменении площади проходного сечения от S 1 до S 2) коэффициент местного сопротивления
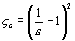 ,
где e – коэффициент сжатия струи, который можно определить по формуле А.Д. Альтшуля: ,
где e – коэффициент сжатия струи, который можно определить по формуле А.Д. Альтшуля:
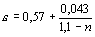 ,
где ,
где 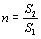 .
Коэффициент местного сопротивления диафрагмы, расположенной внутри трубы постоянного сечения (отнесенный к сечению трубопровода): .
Коэффициент местного сопротивления диафрагмы, расположенной внутри трубы постоянного сечения (отнесенный к сечению трубопровода):
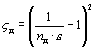 ,
где n д = S o / S – отношение площади отверстия диафрагмы S o к площади сечения трубы S.
При движении жидкости с малыми числами Рейнольдса коэффициенты местных сопротивлений ориентировочно определяют по формуле А.Д. Альтшуля: ,
где n д = S o / S – отношение площади отверстия диафрагмы S o к площади сечения трубы S.
При движении жидкости с малыми числами Рейнольдса коэффициенты местных сопротивлений ориентировочно определяют по формуле А.Д. Альтшуля:
 ,
где ,
где 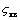 – значение коэффициента местного сопротивления в квадратичной области; Re – число Рейнольдса, отнесенное к нестесненному сечению трубопровода.
Значения параметра А и – значение коэффициента местного сопротивления в квадратичной области; Re – число Рейнольдса, отнесенное к нестесненному сечению трубопровода.
Значения параметра А и 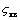 для некоторых местных сопротивлений приведены в приложении (см. табл. П 1.10).
Если расстояние между отдельными местными сопротивлениями достаточно велико для того, чтобы искажение эпюры скоростей, вызванное одним из них, не сказывалось на следующем, потери давления во всех местных сопротивлениях суммируют. Для этого необходимо, чтобы местные сопротивления отстояли друг от друга на расстояние, превышающее l вл, определяемое по формулам:
для турбулентного движения для некоторых местных сопротивлений приведены в приложении (см. табл. П 1.10).
Если расстояние между отдельными местными сопротивлениями достаточно велико для того, чтобы искажение эпюры скоростей, вызванное одним из них, не сказывалось на следующем, потери давления во всех местных сопротивлениях суммируют. Для этого необходимо, чтобы местные сопротивления отстояли друг от друга на расстояние, превышающее l вл, определяемое по формулам:
для турбулентного движения
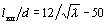 ,
где l – коэффициент трения трубы, на которой расположено местное сопротивление;
при малых числах Рейнольдса ,
где l – коэффициент трения трубы, на которой расположено местное сопротивление;
при малых числах Рейнольдса
 .
55. Механизм турбулизации потока: процесс перемешивания.
Движение отдельных частиц оказывается подобным хаотическому, беспорядочному движению молекул газа. При турбулентном течении векторы скоростей имеют не только осевые, но и нормальные к оси русла составляющие, поэтому наряду с основным продольным перемещением жидкости вдоль русла происходят поперечные перемещения (перемешивание) и вращательное движение отдельных объёмов жидкости. Так возникает перемешивание.
Как показывают опыты ряда исследователей, при турбулентном течении жидкости непосредственно на стенке трубы обычно имеется ламинарный слой .
55. Механизм турбулизации потока: процесс перемешивания.
Движение отдельных частиц оказывается подобным хаотическому, беспорядочному движению молекул газа. При турбулентном течении векторы скоростей имеют не только осевые, но и нормальные к оси русла составляющие, поэтому наряду с основным продольным перемещением жидкости вдоль русла происходят поперечные перемещения (перемешивание) и вращательное движение отдельных объёмов жидкости. Так возникает перемешивание.
Как показывают опыты ряда исследователей, при турбулентном течении жидкости непосредственно на стенке трубы обычно имеется ламинарный слой
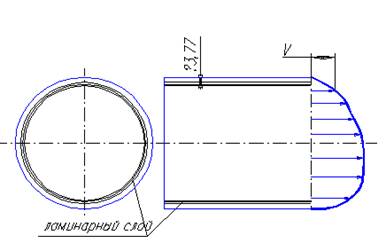 Это очень тонкий слой жидкости, движение в котором является слоистым и происходит без перемешивания. В его пределах скорость круто нарастает от нуля на стенке до некоторой конечной величины
Это очень тонкий слой жидкости, движение в котором является слоистым и происходит без перемешивания. В его пределах скорость круто нарастает от нуля на стенке до некоторой конечной величины 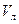 на границе слоя. Толщина на границе слоя. Толщина 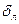 ламинарного слоя крайне невелика, причём оказывается, что число Re, подсчитанное по толщине ламинарного слоя крайне невелика, причём оказывается, что число Re, подсчитанное по толщине 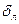 , скорости , скорости 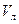 и кинематической вязкости и кинематической вязкости 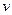 , есть величина постоянная, т.е. , есть величина постоянная, т.е.
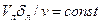 . (1.76)
Эта величина в соответствии с теорией гидродинамического подобия имеет универсальное постоянное значение подобно тому, как постоянно Reкр для течения в трубах. Поэтому при увеличении скорости потока и, следовательно, Re растёт также скорость . (1.76)
Эта величина в соответствии с теорией гидродинамического подобия имеет универсальное постоянное значение подобно тому, как постоянно Reкр для течения в трубах. Поэтому при увеличении скорости потока и, следовательно, Re растёт также скорость 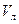 , а толщина , а толщина 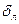 ламинарного слоя уменьшается.
56. Ядро течения и пристенный слой. Кавитация
В некоторых случаях при движении жидкости в закрытых руслах происходит явление, связанное с изменением агрегатного состояния жидкости, т.е. превращение ее в пар с выделением из жидкости растворенных в ней газов.
Наглядно это явление можно продемонстрировать на простом устройстве, состоящим из трубы, на отдельном участке которой установлена прозрачная трубка Вентури (рис.4.2). Вода под давлением движется от сечения 1-1 через сечение 2-2 к сечению 3-3. Как видно из рисунка, сечение 2-2 имеет меньший диаметр. Скорость течения жидкости в трубе можно изменять, например, установленным после сечения 3-3 краном. ламинарного слоя уменьшается.
56. Ядро течения и пристенный слой. Кавитация
В некоторых случаях при движении жидкости в закрытых руслах происходит явление, связанное с изменением агрегатного состояния жидкости, т.е. превращение ее в пар с выделением из жидкости растворенных в ней газов.
Наглядно это явление можно продемонстрировать на простом устройстве, состоящим из трубы, на отдельном участке которой установлена прозрачная трубка Вентури (рис.4.2). Вода под давлением движется от сечения 1-1 через сечение 2-2 к сечению 3-3. Как видно из рисунка, сечение 2-2 имеет меньший диаметр. Скорость течения жидкости в трубе можно изменять, например, установленным после сечения 3-3 краном.
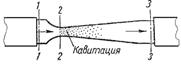 Рис. 4.2. Схема трубки для демонстрации кавитации
При небольшой скорости никаких видимых изменений в движении жидкости не происходит. При увеличении скорости движения жидкости в узком сечении трубки Вентури 2-2 появляется отчетливая зона с образованием пузырьков газа. Образуется область местного кипения, т.е. образование пара с выделением растворенного в воде газа. Далее при подходе жидкости к сечению 3-3 это явление исчезает.
Таким образом, кавитация - это местное нарушение сплошности течения с образованием паровых и газовых пузырей (каверн), обусловленное местным падением давления в потоке.
Кавитация в обычных случаях является нежелательным явлением, и ее не следует допускать в трубопроводах и других элементах гидросистем. Кавитация возникает в кранах, вентилях, задвижках, жиклерах и т.д.
Кавитация может иметь место в гидромашинах (насосах и гидротурбинах), снижая при этом их коэффициент полезного действия, а при длительном воздействии кавитации происходит разрушение деталей, подверженных вибрации. Кроме этого разрушаются стенки трубопроводов, уменьшается их пропускная способность вследствие уменьшения живого сечения трубы.
57. Полуэмпирические теории турбулентности.
Рис. 4.2. Схема трубки для демонстрации кавитации
При небольшой скорости никаких видимых изменений в движении жидкости не происходит. При увеличении скорости движения жидкости в узком сечении трубки Вентури 2-2 появляется отчетливая зона с образованием пузырьков газа. Образуется область местного кипения, т.е. образование пара с выделением растворенного в воде газа. Далее при подходе жидкости к сечению 3-3 это явление исчезает.
Таким образом, кавитация - это местное нарушение сплошности течения с образованием паровых и газовых пузырей (каверн), обусловленное местным падением давления в потоке.
Кавитация в обычных случаях является нежелательным явлением, и ее не следует допускать в трубопроводах и других элементах гидросистем. Кавитация возникает в кранах, вентилях, задвижках, жиклерах и т.д.
Кавитация может иметь место в гидромашинах (насосах и гидротурбинах), снижая при этом их коэффициент полезного действия, а при длительном воздействии кавитации происходит разрушение деталей, подверженных вибрации. Кроме этого разрушаются стенки трубопроводов, уменьшается их пропускная способность вследствие уменьшения живого сечения трубы.
57. Полуэмпирические теории турбулентности.


 58. Коэффициент Дарси при турбулентном движении жидкости, экспериментальные методы его определения.
Для определения значений коэффициентов сопротивлений опытным путём может быть использована, например, установка, изображённая на рис. 1.22 установка состоит из центробежного насоса А, нагнетательной линии В, напорного резервуара С, снабжённого сливной линией D, опытного участка трубопровода Е, приёмного резервуара F и всасывающей линии G.
Во время производства опытов жидкость насосом подаётся в напорный резервуар (в котором благодаря наличию сливной линии поддерживается постоянный уровень) и оттуда поступает в трубопровод.
58. Коэффициент Дарси при турбулентном движении жидкости, экспериментальные методы его определения.
Для определения значений коэффициентов сопротивлений опытным путём может быть использована, например, установка, изображённая на рис. 1.22 установка состоит из центробежного насоса А, нагнетательной линии В, напорного резервуара С, снабжённого сливной линией D, опытного участка трубопровода Е, приёмного резервуара F и всасывающей линии G.
Во время производства опытов жидкость насосом подаётся в напорный резервуар (в котором благодаря наличию сливной линии поддерживается постоянный уровень) и оттуда поступает в трубопровод.
Из трубопровода Е жидкость вытекает в приёмный резервуар и из него по всасывающей линии забирается насосом. Таким образом, во всё время опыта имеет место непрерывная циркуляция жидкости в системе. Измерение расхода жидкости Q осуществляется при помощи водометра Вентури H (в других случаях расход может быть замерен объёмным или весовым способом, для чего между трубопроводом и приёмным резервуаром вводится мерный бак). Линейные потери напора определяются по показанию дифференциального ртутного манометра K. Для большей надёжности измерений целесообразно установить два манометра, взаимно контролирующих друг друга. При этом следует иметь ввиду, что длина опытного участка трубопровода должна быть взята достаточно большой, так как при малой длине разность уровней в коленах ртутного манометра может оказаться незначительной и практически неощутимой; в подобных случаях вместо ртутного манометра необходимо применять дифференциальный пьезометр. При горизонтальном трубопроводе постоянного диаметра линейные потери напора по длине L между сечениями трубопровода a и b, к которым присоединён дифференциальный манометр, определяются выражением
вспоминая, что (где
Из формулы Дарси-Вейсбаха имеем, далее,
где потеря напора
Измерения расхода и напора производятся несколько раз при различных скоростях движения жидкости по трубопроводу. После этого вычисляются соответствующие значения коэффициента Для определения коэффициентов местного сопротивления в трубопроводе устанавливается на фланцах исследуемое сопротивление (расширяющийся или сужающийся патрубок, диафрагма и т.п.) и аналогично предыдущему находится полная потеря напора между сечениями a и b. Предварительно следует найти потерю напора в этом же трубопроводе, при той же самой скорости движения жидкости, но без местного сопротивления. Местная потеря напора
вычисляется значение коэффициента местного сопротивления.
|
|
|
|



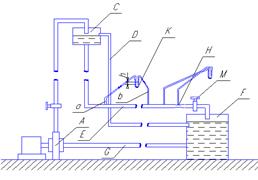 рис. 1.22 Установка для определения коэффициентов сопротивления
рис. 1.22 Установка для определения коэффициентов сопротивления
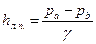 (1.77)
(1.77) (1.78)
(1.78)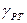 - удельный вес ртути,
- удельный вес ртути, 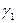 - удельный вес движущейся по трубопроводу жидкости,
- удельный вес движущейся по трубопроводу жидкости,  - разность уровней ртути в манометре), получаем:
- разность уровней ртути в манометре), получаем: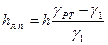 (1.79)
(1.79)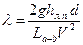 , (1.80)
, (1.80)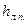 известна, а средняя скорость V может быть вычислена по измеренному расходу жидкости Q:
известна, а средняя скорость V может быть вычислена по измеренному расходу жидкости Q: (1.81)
(1.81)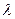 и числа Рейнольдса и строится кривая изменения коэффициента
и числа Рейнольдса и строится кривая изменения коэффициента 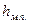 определяется как разность потерь напора в обоих случаях, после чего по формуле
определяется как разность потерь напора в обоих случаях, после чего по формуле (1.82)
(1.82)