Этих границ в нормативно-технической документации.

Пределы допускаемой основной и дополнительных погрешностей определяются разработчиками для каждого типа средств измерений на стадии подготовки производства. В зависимости от назначения средства измерений и характера изменения погрешности в пределах диапазона измерений нормируется для средств измерений различного типа либо предельно-допустимое значение основной абсолютной погрешности, либо предельно-допустимое значение основной приведенной погрешности, либо предельно-допустимое значение основной относительной погрешности.

Для каждого типа средств измерений характер изменения погрешности в пределах диапазона измерений зависит от принципа действия этого средства измерений и может быть самым разнообразным. Однако, как показала практика, среди этого многообразия часто удается выделить три типовых случая, предопределяющих выбор формы представления пределов допускаемой погрешности. Типовые варианты отклонения реальных передаточных характеристик средств измерений от номинальной характеристики и соответствующие им графики изменения предельных значений абсолютной и относительной погрешностей в зависимости от измеряемой величины приведены на рис 2.

 

 

 

Если реальная передаточная характеристика средства измерений смещена по отношению к номинальной (1-й график на рис.2а), абсолютная погрешность, возникающая при этом, (1-й график на рис.2б), не зависит от измеряемой величины.

 

Составляющую погрешности средства измерений, не зависящую от измеряемой величины, называют аддитивной погрешностью.

Если угол наклона реальной передаточной характеристики средства измерений отличается от номинального (2-й график на рис. 2а), то абсолютная погрешность будет линейно зависеть от измеряемой величины (2-й график на рис. 2б).

 

Составляющую погрешности средства измерений, линейно зависящую от измеряемой величины, называют мультипликативной погрешностью.

Если реальная передаточная характеристика средства измерений смещена по отношению к номинальной и угол ее наклона отличается от номинального (3-й график на рис. 2а), то в этом случае имеет место как аддитивная, так и мультипликативная погрешность.

Аддитивная погрешность возникает из-за неточной установки нулевого значения перед началом измерений, ухода нуля в процессе измерений, из-за наличия трений в опорах измерительного механизма, из-за наличия термо-эдс в контактных соединениях и т.д.

Мультипликативная погрешность возникает при изменении коэффициентов усиления или ослабления входных сигналов (например, при изменении температуры окружающей среды, или вследствие старения элементов), из-за изменения значений, воспроизводимых мерами, встроенными в измерительные приборы, из-за изменений жесткости пружин, создающих противодействующий момент в электромеханических приборах и т.д.

Ширина полосы неопределенности значений абсолютной (рис.2б) и относительной (рис.2в) погрешностей характеризует разброс и изменение в процессе эксплуатации индивидуальных характеристик множества находящихся в обращении средств измерений определенного типа.

 

А) Нормирование пределов допускаемой основной погрешности для

средств измерений с преобладающей аддитивной погрешностью.

Для средств измерений с преобладающей аддитивной погрешностью (1-й график на рис.2) удобно нормировать одним числом предельно-допустимое значение абсолютной погрешности (∆_max= ±а). В этом случае фактическая абсолютная погрешность ∆ каждого экземпляра средства измерений данного типа на различных участках шкалы может иметь различные значения, но не должна превышать предельно-допустимой величины (∆ ≤ ±а). В многопредельных измерительных приборах с преобладающей аддитивной погрешностью для каждого предела измерений пришлось бы указывать свое значение предельно допустимой абсолютной погрешности. К сожалению, как видно из 1-го графика на рис.2в, нормировать одним числом предел допускаемой относительной погрешности в различных точках шкалы не представляется возможным. По этой причине для средств измерений с преобладающей аддитивной погрешностью часто нормируют одним числом значение так называемой основной приведеннойотносительной погрешности

,

где X_N – нормирующее значение.

Таким способом, например, нормируются погрешности большинства электромеханических и электронных приборов со стрелочными индикаторами. В качестве нормирующего значения X_N обычно используется предел измерений (X_N = X_max), удвоенное значение предела измерений (если нулевая отметка находится в середине шкалы), или длина шкалы (для приборов с неравномерной шкалой). Если X_N = X_max, то значение приведенной погрешности γ равно пределу допускаемой относительной погрешности средства измерений в точке, соответствующей пределу измерений. По заданному значению предела допускаемой основной приведенной погрешности легко определить предел допускаемой основной абсолютной погрешности для каждого предела измерений многопредельного прибора: .

После этого для любой отметки шкалы X может быть произведена оценка предельно-допустимой основной относительной погрешности:

.

 

Б) Нормирование пределов допускаемой основной погрешности для

средств измерений с преобладающей мультипликативной

погрешностью.

Как видно из рис.2 (2-й график), для средств измерений с преобладающей мультипликативной погрешностью, одним числом удобно нормировать предел допускаемой основной относительной погрешности (рис.2в) δ_max= ± b∙100%. В этом случае, фактическая относительная погрешность каждого экземпляра средства измерений данного типа на различных участках шкалы может иметь различные значения, но не должна превышать предельно допустимой величины (δ ≤ ± b∙100%). По заданному значению предельно допустимой относительной погрешности δ_max для любой точки шкалы может быть произведена оценка предельно-допустимой абсолютной погрешности:

.

К числу средств измерений с преобладающей мультипликативной погрешностью относится большинство многозначных мер, счетчики электрической энергии, счетчики воды, расходомеры и др. Следует отметить, что для реальных средств измерений с преобладающей мультипликативной погрешностью не удается полностью устранить аддитивную погрешность. По этой причине в технической документации всегда указывается наименьшее значение измеряемой величины, для которого предел допускаемой основной относительной погрешности ещё не превышает заданного значения δ_max. Ниже этого наименьшего значения измеряемой величины погрешность измерений не нормируется и является неопределенной.

 

В) Нормирование пределов допускаемой основной погрешности для

средств измерений с соизмеримой аддитивной и мультипликативной

погрешностью.

 

Если аддитивная и мультипликативная составляющая погрешности средства измерений соизмеримы (3-й график на рис.2), то задание предельно-допустимой погрешности одним числом не представляется возможным. В этом случае либо нормируется предел допускаемой абсолютной основной погрешности (указываются предельно-допустимые значения a и b), либо (чаще всего) нормируется предел допускаемой относительной основной погрешности. В последнем случае численные значения предельно-допустимых относительных погрешностей в различных точках шкалы оцениваются по формуле:

,

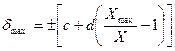где X_max – предел измерений;

X - измеренное значение;

d = - значение приведенной к пределу измерений

аддитивной составляющей основной погрешности;

с = - значение результирующей относительной

основной погрешности в точке, соответствующей пределу

измерений.

 

Рассмотренным выше способом (указанием численных значений c и d) нормируются, в частности, предельно-допустимые значения относительной основной погрешности цифровых измерительных приборов. В этом случае относительные погрешности каждого экземпляра средств измерений определенного типа не должны превышать установленных для этого типа средств измерений значений предельно-допустимой погрешности:

.

При этом абсолютная основная погрешность определяется по формуле

.

 

Г) Нормирование дополнительных погрешностей.

Наиболее часто пределы допускаемых дополнительных погрешностей указывают в технической документации либо одним значением для всей рабочей области величины, влияющей на точность средства измерений (иногда несколькими значениями для поддиапазонов рабочей области влияющей величины), либо отношением предела допускаемой дополнительной погрешности к интервалу значений влияющей величины. Пределы допускаемых дополнительных погрешностей указываются на каждой, влияющей на точность средства измерений величине. При этом, как правило, значения дополнительных погрешностей устанавливают в виде дольного или кратного значения предела допускаемой основной погрешности. Например, в документации может быть указано, что при температуре окружающей среды за пределами нормальной области температур, предел допускаемой дополнительной погрешности, возникающей по этой причине, не должен превышать 0,2% на 10^о С.

 

Классы точности средств измерений.

 

Исторически по точности средства измерений подразделяют на классы. Иногда их называют классами точности, иногда классами допуска, иногда просто классами.

 

Класс точности средства измерений – это его характеристика, отражающая точностные возможности средств измерений данного типа.

Допускается буквенное или числовое обозначение классов точности. Средствам измерений, предназначенным для измерения двух и более физических величин, допускается присваивать различные классы точности для каждой измеряемой величины. Средствам измерений с двумя или более переключаемыми диапазонами измерений также допускается присваивать два или более класса точности.

Если нормируется предел допускаемой абсолютной основной погрешности, или в различных поддиапазонах измерений установлены разные значения пределов допускаемой относительной основной погрешности, то, как правило, применяется буквенное обозначение классов. Так, например платиновые термометры сопротивления изготовляют с классом допуска А или классом допуска В. При этом для класса А установлен предел допускаемой абсолютной основной погрешности , а для класса В - , где 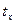– температура измеряемой среды.

Если для средств измерений того или иного типа нормируется одно значение предельно-допустимой приведенной основной погрешности, или одно значение предельно-допустимой относительной основной погрешности, или указываются значения c и d, то для обозначения классов точности используются десятичные числа. В соответствии с ГОСТом 8.401-80 для обозначения классов точности допускается применение следующих чисел:

1∙10ⁿ; 1,5∙10ⁿ; 2∙10ⁿ; 2,5∙10ⁿ; 4∙10ⁿ; 5∙10ⁿ; 6∙10ⁿ, где n = 0, -1, -2, и т.д.

Для средств измерений с преобладающей аддитивной погрешностью численное значение класса точности выбирается из указанного ряда равным предельно-допустимому значению приведенной основной погрешности, выраженной в процентах. Для средств измерений с преобладающей мультипликативной погрешностью численное значение класса точности соответствует пределу допускаемой относительной основной погрешности также выраженной в процентах. Для средств измерений с соизмеримыми аддитивными и мультипликативными погрешностями числа с и d также выбираются из указанного выше ряда. При этом класс точности средства измерений обозначается двумя числами, разделенными косой чертой, например, 0,05/0,02. В этомслучае с = 0,05%; d = 0,02%. Примеры обозначений классов точности в документации и на средствах измерений, а также расчетные формулы для оценки пределов допускаемой основной погрешности приведены в Таблице 1.

 

Правила округления и записи результата измерений.

Нормирование пределов допускаемых погрешностей средств измерений производится указанием значения погрешностей с одной или двумя значащими цифрами. По этой причине при расчете значений погрешностей измерений также должны быть оставлены только первые одна или две значащие цифры. Для округления используются следующие правила:

1. Погрешность результата измерения указывается двумя значащими цифрами, если первая из них не более 2, и одной цифрой, если первая из них 3 и более.

2. Показание прибора округляется до того же десятичного разряда, которым заканчивается округленное значение абсолютной погрешности.

3. Округление производится в окончательном ответе, промежуточные вычисления выполняют с одной – двумя избыточными цифрами.

 

Пример 1:

- показание прибора - 5,361 В;

- вычисленное значение абсолютной погрешности - ± 0,264 В;

- округленное значение абсолютной погрешности - ± 0,26 В;

- результат измерения - (5,36 ± 0,26) В.

 

Таблица 1

Примеры обозначения классов точности средств измерений и расчетные

формулы для оценки пределов допускаемой основной погрешности.

 

Форма представления нормируемой основной погрешности	Примеры обозначения класса точности	Расчетные формулы для оценки пределов допускаемой основной погрешности	Примечания
В документации	На средствах измерений
Нормируется предел допускаемой абсолютной основной погрешности	Варианты: - класс B; - класс допуска В; -класс точности В.	В	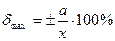или   или	Значения aи b приводятся в документации на средство измерений.
Нормируется предел допускаемой приведенной основной погрешности	Варианты: - класс точности 1,5   2,5 - не обозначается.	1,5	где предел измерений.	Для приборов с равномерной шкалой и нулевой отметкой в начале шкалы
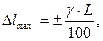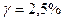
Варианты: - класс точности 2,5; - не обозначается		- предел допускаемой абсолютной погрешности в мм. - длина всей шкалы.	Для приборов с неравномерной шкалой. Длина шкалы указывается в документации.
Нормируется предел допускаемой относительной основной погрешности	Класс точности 0,5.	0,5		Для средств измерений с преобладающей мультипликативной погрешностью.
Варианты: - класс точности 0,02/0,01; -не обозначается.	0,02/0,01		Для средств измерений с соизмеримыми аддитивной и мультипликативной погрешностью

Пример 2:

- показание прибора – 35,67 мА;

- вычисленное значение абсолютной погрешности - ± 0,541 мА;

- округленное значение абсолютной погрешности - ± 0,5 мА;

- результат измерений – (35,7 ± 0,5) мА.

Пример 3:

- вычисленное значение относительной погрешности – ± 1,268 %;

- округленное значение относительной погрешности – ± 1,3 %.

Пример 4:

- вычисленное значение относительной погрешности - ± 0,367 %;

- округленное значение относительной погрешности - ± 0,4 %.

 

 

II.2. Вопросы для самопроверки

1. Чем вызываются погрешности измерений?

2. Перечислите разновидности погрешностей, возникающих в процессе измерений?

3. Какая разница между абсолютной, относительной и приведенной погрешностями измерения и в чем смысл их введения?

4. Чем отличается основная погрешность измерения от дополнительной?

5. Чем отличается методическая погрешность измерения от инструментальной?

6. Чем отличается систематическая погрешность измерения от случайной?

7. Что понимается под аддитивной и мультипликативной оставляющими погрешности?

8. В каких случаях целесообразно использовать статистическую обработку результатов измерений?

9. Какие статистические характеристики обработки наиболее часто используются на практике?

10. Как оценивается неисключенная систематическая погрешность при статистической обработке результатов измерений?

11. Что характеризует величина среднеквадратического отклонения?

12. В чем заключается суть понятий «доверительной вероятности» и «доверительного интервала», используемых при статистической обработке результатов измерений?

13. В чем заключается разность понятий «погрешность измерения» и

«погрешность средства измерения»?

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: