 |
Система уравнений Максвелла.
|
|
|
|
Самоиндукция. Коэффициенты индуктивности.
Всякий ток в проводнике создает магнитное поле. Но это поле, начав изменяться, в свою очередь влияет на вызвавший его ток. Это явление называется самоиндукцией.
Если в пространстве нет ферромагнетиков, то магнитный поток через виток с током пропорционален протекающему в нем току L и носит название коэффициента самоиндукции провода. Он зависит только от размеров и конфигурации проводника. Тогда закон электромагнитной индукции будет следующим (Ф = LI):
.
Для длинного соленоида L вычисляется и равно
, где n — плотность витков на единицу длины, а V=Sl — объем пространства внутри соленоида.
В системе СИ единицей измерения коэффициента самоиндукции является Гн (1Гн = 1В*с/А).
Если рядом расположенных проводников с токами много, то кроме коэффициентов самоиндукции вводятся коэффициенты взаимной индукции, которые описывают часть ЭДС индукции, возникающей под воздействием другого тока
.
Коэффициенты взаимной индукции также измеряются в Гн.
Энергия магнитного поля.
Проводник, по которому протекает электрический ток, создает в окружающем пространстве магнитное поле, которое появляется и исчезает вместе с появлением и исчезновением тока.
Магнитное поле является носителем энергии. Естественно предположить, что энергия магнитного поля равна работе, которая затрачивается током на создание этого поля.
Рассмотрим контур индуктивностью L, по которому течет ток I. С данным контуром сцеплен магнитный поток Ф = LI, причем при изменении тока на dI магнитный поток изменяется на dФ = LdI. Однако для изменения магнитного потока на величину dФ необходимо совершить работу. Тогда
|
|
|
работа по созданию магнитного потока будет
Следовательно, энергия магнитного поля, связанного с контуром,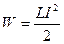 
Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия 
(где V = SI — объем соленоида) заключена в объеме соленоида и распределена в нем
с постоянной объемной плотностью 
Ток смещения.
Согласно Максвеллу, если всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, то должно существовать и обратное явление: всякое
изменение электрического поля должно вызывать появление в окружающем пространстве вихревого магнитного поля. Для установления количественных отношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел ток смещения.
Рассмотрим цепь переменного тока, содержащую конденсатор.
Между обкладками заряжающегося и разряжающегося конденсатора имеется переменное электрическое поле, поэтому через конденсатор «протекают» токи смещения, причем в тех участках, где отсутствуют проводники. Найдем количественную связь между изменяющимся электрическим и вызываемым им магнитным полями.
По Максвеллу, переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, как если бы между обкладками конденсатора существовал ток смещения, равный току в подводящих проводах. Тогда можно утверждать, что токи проводимости I и смещения Iсм равны:
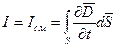
Выражение 
было названо Максвеллом плотностью тока смещения.
Из всех физических свойств, присущих току проводимости, Максвелл приписал току смещения лишь одно — способность создавать в окружающем пространстве магнитное поле.
Система уравнений Максвелла.
В основе теории Максвелла лежат четыре уравнения:
1. Электрическое поле может быть как потенциальным (EQ), так и вихревым (Ев), поэтому напряженность суммарного поля Е = EQ + Ев. Так как циркуляция вектора EQ равна нулю, а циркуляция вектора Ев определяется выражением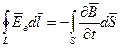 
, то циркуляция вектора напряженности суммарного поля 
.
|
|
|
Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.
2. Обобщенная теорема о циркуляции вектора Н:
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
3. Теорема Гаусса для поля D:
Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью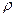 
, то:
4. Теорема Гаусса для поля В:
Итак, полная система уравнений Максвелла в интегральной форме:
Величины, входящие в уравнения Максвелла, не являются независимыми.
Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут
возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но отсутствуют магнитные.
Для стационарных полей (Е — const и В — const) уравнения Максвелла примут вид:
т.е. источниками электрического поля в данном случае являются только электрические заряды, а источниками магнитного — только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля
|
|
|
