Электрические измерительные преобразователи

3.2.1. Основные определения и формулы

 

Для преобразования электрических сигналов из одной формы в другую, более удобную при дальнейшем их применении с другими средствами измерений используются электрические измерительные преобразователи.

Типичными представителями этих средств измерения являются делители напряжения резисторного, емкостного, индуктивного типа, шунты, добавочные сопротивления, измерительные трансформаторы тока (ТТ) и напряжения (ТН), выпрямительные измерительные преобразователи, термочувствительные элементы.

 

Для расширения предела измерения по току измерительных приборов магнитоэлектрической системы применяются шунты, которые включаются параллельно прибору и имеют два токовых (ТТ) и два потенциальных зажима (ПП).

Основными параметрами измерительных приборов являются: 1) номинальный ток - Iн; 2) номинальное напряжение - Uн; 3) выходное (собственное) сопротивление измерительного механизма. Эти три параметра связаны между собой законом Ома:

R_им = U_н / I_н (3.8)

При использовании наружного шунта, его присоединяют к прибору укороченными проводами с предварительно рассчитанным сечением, чтобы сопротивление провода было значительно меньше сопротивления Rш.

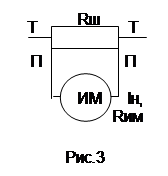Измеряемый ток Iх подводится к шунту (зажимы ТТ), а измерительный механизм подключается к зажимам ПП (рис. 3). Нужно помнить, что если провода цепи с измеряемым током Ix > Iн, присоединить непосредственно к прибору, то при случайном отключении шунта измеряемый ток Ix будет протекать через измерительный механизм, что вызовет выход его из строя.

Для расчета сопротивления шунта обычно применяются формулы:

Rш = Rим/(n-1), (3.9)

Rш = Uн / Iш = Uн / (Ix - Iн), (3.10)

где Rим - входное сопротивление прибора, n = Ix / Iн - коэффициент преобразования измеряемого тока (коэффициент шунтирования).

Основные трудности при расчете сопротивлений шунтов возникают при расширении пределов измерений многопредельных приборов. Эти приборы переносного исполнения обеспечиваются многопредельными шунтами, которые включают несколько резисторов, переключаемых в зависимости от пределов измерения (рис. 4, 5). Схема, представленная на рис. 4 (расчет сопротивлений шунтов ведется по формулам (3.9) или (3.10)) из-за влияния контактных переходных сопротивлений и возможности перегрузки измерительного механизма широко не применяется. В схеме прибора на рис. 5 используется универсальный шунт, причем при измерении тока I1 в качестве шунта применен резистор Rш1, а резисторы Rш2 и Rш3 включены последовательно с измерительным механизмом (Rим) и здесь удобнее при расчете пользоваться формулой (3.10).

 

 

 

 

Рис. 4 Рис. 5

Добавочные сопротивления Rд применяют для расширения пределов измерения в ольтметра и исключения влияния температуры на изменение сопротивления его измерительного механизма Rим (рис. 6). В качестве Rд применяются точные малогабаритные проволочные и микропроволочные резисторы и непроволочные резисторы повышенной

 

стабильности, и высокоточные, изготовляемые с допуском ± 0,1% (минимальный ТКС в заданном диапазоне температур). Как и при расчете Rш можно применять для определения значения Rд формулы:

R_д = R_им (m-1), (3.11)

R_д = U_д / I_н = (U_x -U_н) / I_н 3.12)

где m = Ux / Uн, Ux - предельное измеряемое напряжение при данном Rд.

На практике обычно используют многопредельные вольтметры постоянного тока. В качестве ИМ таких вольтметров находят широкое применение высокочувствительные микроамперметры с номинальным током Iн=50–100мкА, известным сопротивлением Rим, по которым можно определить номинальное напряжение Uн=Iн*Rим. Для таких вольтметров сопротивление добавочного резистора

R_д=U_х/I_н-R_им. (3.13)

Многопредельный вольтметр, как и многопредельный амперметр, можно выполнить с отдельными добавочными резисторами (рис. 7) для каждого предела, когда Rд рассчитывают по формулам (3.11-3.13), а можно так, как показано на рис. 8.

Результаты расчета показывают, что входное сопротивление вольтметра изменяется при изменении предела измерения. Поэтому многопредельные вольтметры характеризуют относительным входным сопротивлением Rвх.о, численно равным сопротивлению, приходящемуся на 1В предельного значения.

Основным достоинством магнитоэлектрических ИМ является их высокая чувствительность и точность при измерении на постоянном токе. Для использования этих приборов при измерении переменных токов и напряжений необходимо применять выпрямительные измерительные преобразователи, основанные на базе полупроводниковых диодов. В таких приборах измеряемое переменное напряжение или ток преобразуется в пульсирующее одной полярности, средневыпрямленное значение которого, (постоянная составляющая) измеряется магнитоэлектрическим ИМ.

 

Рис. 7 Рис. 8

Выпрямительные измерительные преобразователи выполняются по одно- (рис.9) или двухполупериодной схемам (рис.10). В первой схеме ток через ИМ протекает один раз в течение периода, когда на аноде VD1 появляется положительный полупериод напряжения, а при отрицательном полупериоде ток протекает через диод VD2 и резистор R, величина которого равна Rим, что обеспечивает равенство сопротивления прибора току обоих направлений, то есть одинаково для обоих полупериодов. Для схемы на рис.10 выпрямленный ток протекает через ИМ дважды за период. При этом чувствительность прибора повышается в два раза по сравнению с однополупериодным выпрямлением, но увеличивается погрешность при изменении температуры окружающей среды. Поэтому часто применяют выпрямители с несимметричной мостовой схемой, в которой два диода VD3, VD4, (VD1, VD3) заменяют резисторами.

Основными параметрами переменных токов и напряжений являются их амплитудные (Im, Um), среднеквадратичные (I,U) и средневыпрямленные (Iсв, Uсв) значения, которые связаны между собой через коэффициенты формы и амплитуды

К_ф = I / I_св (U/U_св); K_a = I_м / I (U_м/U) (3.14)

 

 

 

 

Рис. 9 Рис. 10

 

Значения коэффициентов Кф и Ка для распространенных на практике форм кривых токов и напряжений приведены в таблице 2.

В приборе с однополупериодной схемой выпрямления через его измерительный механизм ИМ протекает ток

амплитуды:

I_им = I_св = I_m / p = Ö2 *I / p. (3.15)

Для двухполупериодной схемы:

I_им = I_св =2* I_m / p = 0,9 *I 3.16)

Выпрямительные приборы обычно градуируются в среднеквадратичных (действующих) значениях синусоидального напряжения или тока. При градуировке выпрямительный прибор включают в цепь переменного синусоидального тока. Полученный при этом результат измерения по шкале измерителя магнитоэлектрической системы (ИМ) умножается на 2,22 - при однополупериод­ной и на 1,11 - при двухполупериодной схеме выпрямления и наносится на шкалу выпрямительного прибора. Значения коэффициентов определяют соотношения параметров переменного синусоидального тока (напряжения) с учетом схемы выпрямления.

Для однополупериодной схемы I = Iсв * 2Кф =Iсв *2*1,11=2,22*Iсв.

Для двухполупериодной схемы I = Iсв *Кф = 1,11*Iсв,

где Кф =I/Iсв - коэффициент формы для синусоидального тока или напряжения, равный 1,11 - для двухполупериодной схемы выпрямления.

Таблица 2

№	Форма тока, напряжения	График тока, напряжения	Коэффициенты
формы Кф	ампли­туды Ка
1	Синусоидальная		1,11	1,41
	Пульсирующая на выходе двух­ полупериодного выпрямителя		1,11	1,41
	Пульсирующая на выходе одно­ полупериодного выпрямителя		1,57	2,0
	Пилообразная треугольная		1,16	1,73
	Прямоугольная симметричная		1,0	1,0
	Прямоугольная однополярная

 

При измерении несинусоидальных токов или напряжений необходимо в результат измерения отсчета по шкале прибора ввести поправку путем соответствующего пересчета показаний прибора с учетом коэффициента формы измеряемого тока (См. пример 3.,14). Предельное среднеквадратичное значение I_пред синусоидального переменного тока для приборов с однополупериодной схемой выпрямления определяется из соотношения

I_пред = I_ном * 2К_ф = 2,22*I_ном; (3.17)

с двухполупериодной I_пред = I_ном * К_ф = 1,11*I_ном (3.18)

 

2.2. Примеры решения задач

 

Пример 3.7. Имеется микроамперметр М260М с номинальным током Iн=100 мкА и Rим=2000 Ом и шкалой имеющей 20 делений. Необходимо этим прибором измерить ток Iх < 10 мА.

Решение:

Rш=Rим / (n-1)=2000/((10*10^-3/100*10^-6)-1) = 20,2 Ом;

Второй метод: так как Iш= Iх-Iн = 10*10^-3 - 0,1*10^-3 = 9,9*10^-3А, а номинальное напряжение Uн = Iн*Rим = 100*10 ^-6*2*10³= 200*10^-3 В, то Rш =Uн/Iш = 200*10 ^-3/9,9*10 ^-3= 20,2 Ом.

При фиксировании результата измерения необходимо учитывать, что с применением Rш изменяется предел измерения по току, а следовательно и цена деления шкалы прибора. Так для М260М цена деления (постоянная прибора) C_I=5мкА/дел, а при подключении Rш=20,2 Ом C_II=0,5мА/дел.

 

Пример 3.8. Рассчитать сопротивления резисторов Rш1, Rш2, Rш3 многопредельного универсального шунта (рис.5) для измерения токов с пределами: I1 = 30 мА, I2 = 3,0 мА, I3 = 0,3 мА с помощью измерительного механизма с Iн = 150 мкА и Rим = 1500 Ом.

Решение:

1) Rш1+Rш2+Rш3=IнRим/(I3-Iн)=150*10^–6*1500/(0,3*10^–3– 0,15*10^–3)=1500Ом

2) Rш1=Iн(Rим+Rш1+Rш2+Rш3)/I1=Iн*SR/I1=150*10^–6 (1500+1500)/(30*10^–3)=15Ом

3) Rш1 + Rш2 = IнSR/I2 = 150*10^–6 *3000/(3*10^–3)= 150 Ом

4)Rш2 = (Rш1+Rш2)-Rш2 = 150 - 15 = 135 Ом

5)Rш3 = (Rш1+Rш2+Rш3)-(Rш1+Rш2) = 1500-150 = 1350 Ом.

Использование формулы(3.9) требует решения системы уравнений

Iн = I1Rш1/ SR = I2(Rш1+Rш2)/ SR = I3(Rш1+Rш2+Rш3)/ SR...;

Rш1= I3*Iн*Rим/I1(I3 - Iн)...;

Rш2 = (I1-I2)I3*Iн*Rим/(I2 - Iн)I2*I1...;

Rш3 = (I2-I3)Iн*Rим/(I3 - Iн)I2....

 

Пример 3.9. Пределы измерения милливольтметра типа М24-155: Iн=6 мА, Uн=100 мВ. Шкала прибора 100 дел. Необходимо измерить напряжение Uх=I В. Требуется рассчитать величину добавочного сопротивления Rд (рис. 6) и определить изменение цены деления шкалы прибора.

Решение:

1) Rим=Uн/Iн=16,66 Ом; m=Uх/Uн=1/(100*10^–3)=10;

по формуле (3.11) Rд=16,667*9=150 Ом

(по формуле (3.12) Rд = (1– 0,1) / (6*10^–3)=150 Ом).

2) За счет Rд цена деления изменяется с 1 до 10 мВ/дел;

3) Входное сопротивление прибора становится равным

Rвх=Rим+Rд=16,667+150 = 166,97 Ом

 

Пример 3.10. Рассчитать значения сопротивлений добавочных резисторов по схеме на рис.8 для трех пределов измерений: 1B, 5В, 10В, если ИМ - микроамперметр с Iн = 100 мкА и Rим = 1000 Ом.

Решение:

Для предела 1B Rд1=Un1 / Iн – Rим=I/(100*10^–6)–1000=9000 Ом;

Для предела 5В Rд1+Rд2=Un2 /Iн – Rим=5/(100*10^–6)–1000=49 кОм;

Rд2=49 – 9=40 кОм.

Для предела 10В Rд1+Rд2+Rд3=Un /Iн – Rим=10/100*10 5-6 0-1000 кОм;

Rд3=99-49=50 кОм.

 

Пример 3.11. При измерении несинусоидального тока с коэффициентом Кфх получены показания по шкале выпрямительного амперметра: Iα1– для однополупериодной, Iα2 – для двухполупериодной схем выпрямления. Определить действующие значения.

Решение.

Среднеквадратичное значение измеряемого тока Iх:

Iх1=Iα1*Кфх/2Кф=Iα*Кфх/2,22; Iх2 =Iα2*Кфх/Кф=Iф2*Кфх/1,11.

 

Пример 3.12. В цепь переменного синусоидального тока с амплитудой Im = 15,5 мА включен выпрямительный миллиамперметр с однополупериодной схемой выпрямления (рис.9). Определить: 1) Значение постоянного тока, протекающего через измеритель ИМ; 2) Показание миллиамперметра, шкала которого градуирована в среднеквадратичных значениях синусоидального тока.

Решение.

1) Средневыпрямленное значение тока, протекающего через ИМ:

Iсв = Im/ p = 15,5/3,14 = 4,96 мА.

2) Показание прибора с учетом градуировки шкалы:

Iα =Iсв*2Кф=4,96*2,22=11 мА. (Действительно, I=ImÖ2 =15,5Ö2 = 11мА.)

 

Пример 3.13. Решить пример 3.12, если миллиамперметр имеет двухполупериодную схему выпрямления (рис.10).

Решение.

1) Средневыпрямленное значение тока через ИМ:

Iсв = 2Im / p = 2*15,5/3,14 = 9,92 мА.

2) Показание прибора с учетом градуировки шкалы Iα =Iсв*Kф=9,92*1,11=11 мА, что соответствует среднеквадратичному значению измеряемого тока.

Пример 3.14. В цепь переменного тока треугольной формы (рис.11) с параметрами Im = 50 мА, f = 100 гц включен выпрямительный миллиамперметр с двухполупериодной схемой выпрямления. Шкала градуирована в среднеквадратичных значениях синусоидального тока. Определить: 1)показание прибора; 2)действительное значение измеряемого тока.

Решение.

Для подобной формы тока Кфх = 1,16, Ках = 1,73.

Значит I = Im / Kax = 0,578*Im, Icв = I/Kфх = 0,578Im/1,16 = 0,5Im.

1) Показание прибора Iα = Iсв*Kф = 0,5*50*1,11 = 27,8 мА.

2) Действительное значение измеряемого тока

I = Iα *Кфх /Кф=27,8*1,16/1,11=29 мА.

 

Пример 3.15. Выпрямительный миллиамперметр с однополупериодной схемой выпрямления включен в цепь однополярных прямоугольных импульсов тока (рис.12) с параметрами Im = 25мА, t 4и 0 = 100мкс, T 4и 0 = 1 мс. Шкала градуирована в среднеквадратичных значениях синусоидального тока. Определить: 1)показания прибора; 2)действительное значение измеряемого тока, определяемое его формой, для которой:

Решение.

Iсв = I / Kфх; I = Im/Kах; Kах = Kфх =ÖTи / tи = ÖQ

1)Показания прибора

Iα =Iсв*2Kф=Im(tи / Ти)*2Кф=25*[100*10^-6/(1*10 ^–3)]*2*1,11=5,55 мА

2)Действительное значение измеряемого тока

Iх =(Iф / Кф)*Kфx =5,55*3,16/(2*1,11) = 7,9 мА

 

 

Рис. 11 Рис. 12

 

 

3.3. Измерительные мосты

3.3.1. Основные определения и формулы

 

Важным видом измерительных цепей являются мостовые цепи. В них можно выделить три ветви (рис.13): диагональ питания П, диагональ указателя равновесия Г (нулевая ветвь) и ветвь измеряемого сопротивления (датчика) Д. Основными характеристиками моста являются его входные сопротивления со стороны диагоналей питания Zп_Вх0 и указателя равновесия Zг_Вх0, взаимное сопротивление ветви указателя равновесия и ветви измеряемого сопротивления Z1г'.

Для уравновешенного моста

Zп_Вх = [(Z1 ₀ +Z2)(Z3 +Z4)]/(Z1 ₀ +Z2 +Z3+Z4)=

=Z1 ₀ (1+m)*n/(1+n); (3.19)

Zг_Вх0 = [(Z1 ₀ +Z3)(Z2 +Z4)]/(Z1 ₀ +Z2+Z3+Z4)=

=Z1 ₀ (1+n)*m/(1+m); (3.20)

Z1г' = Z1 ₀ (1+n) (3.21)

где Z1₀ - значение Z1 при равновесии моста; m = Z2/Z1₀; n = Z3 /Z1₀.

Еще одной важной характеристикой мостовой схемы является чувствительность. Определяют ее значение по току, напряжению и мощности вблизи состояния равновесия моста.

Эквивалентная схема катушки индуктивности содержит последовательно включаемое сопротивление (сопротивление провода, которым наматывается катушка), а эквивалентная схема конденсатора - последовательно или параллельно включаемые сопротивления потерь и утечки соответственно. Для их оценки используются понятия добротности Q и тангенса угла потерь tg d:

для схемы рис.14 Q= w *L1 / R1 = 1/ (w *C4 *R4) (3.29)

tg d = w * C4 * R4 (3.30)

для схемы рис.15 Q= = w *L1 / R1 = w *C4 *R4 (3.31)

tg d =1/ (w * C4 * R4) (3.32)

 

 

 

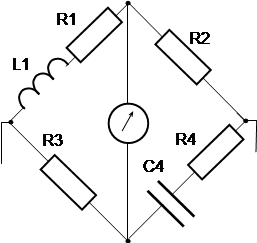Рис. 14 Рис. 15

 

Равновесие моста имеет место при подборе плеч таким образом, чтобы ток в диагонали указателя равновесия отсутствовал, т.е. при

Z1Z4 =Z2Z3, (3.22)

где Z1,Z2,Z3,Z4 - полное сопротивление соответствующих плеч моста.

Полное комплексное сопротивление i-го плеча может быть выражено в алгебраической или показательной форме, т.е.

Zi =Ri +jXi или Zi =zi *e ^jji , (3.23)

где Ri,Xi - активное и реактивное сопротивление i-го плеча; zi - модуль полного сопротивления i-го плеча; ji - угол сдвига тока относительно напряжения i-го плеча.

Соответственно в алгебраической и показательной форме могут быть представлены и условия равновесия моста:

R1R4 – X1X4 = R2R3 – X2X3 (3.24)

R1X4 + X1R4 = R2X3 + X2R3 (3.25)

z1 * z4 = z2 * z3 (3.26)

j1+ j4 = j 2 + j 3 (3.27)

Наличие двух уравнений означает необходимость регулирования не менее двух параметров моста переменного тока для достижения его равновесия. Существуют различные схемы уравновешивания моста (рис. 14-19).

Мост постоянного тока (рис. 20) можно рассматривать как частный случай моста переменного тока. Условие равновесия моста постоянного тока:

R1*R4 =R2 * R3 (3.28)

 

 

Рис. 16 Рис. 17

 

 

Рис. 18 Рис. 19

 

 

3.3.2. Примеры решения задач

Пример 3.16. На рис.20 представлена уравновешенная мостовая цепь постоянного тока. Определить R1, если известно, что R2 = 100 Ом, R3 = 25 Ом, R4 = 50 Ом.

Решение.

Условие равновесия моста постоянного тока имеет вид:

R1*R4 = R2*R3,

откуда R1 = R2*R3/R4 = 100*25/50 = 50 Ом.

 

Пример 3.17. Известны значения плеч моста (рис.20): R2 = 10 Ом; R3 = 1500 Ом; R4 = 1000 Ом; Rг = 100 Ом; Rп = 10 Ом. Определить: 1)сопротивление R1 при котором мост уравновешен; 2) входное сопротивление моста со стороны диагонали питания Rп.п.; 3)входное сопротивление моста со стороны диагонали указателя равновесия Rг.г.; 4)взаимное сопротивление между ветвью измеряемого сопротивления и ветвью указателя равновесия R1Г. Пункты 2, 3, 4 определить для уравновешенной мостовой цепи.

Решение.

Сопротивления R1, Rп.п., Rг.г. определяются по формулам:

R1= R2*R3/R4 = 10*1500/1000 = 15 Ом;

Rп.п.=Rп + R 4п.вхо = Rп + R1*n(1+m)/(1+n) = 34,75 Oм;

Rг.г.=Rг +Rг.вхо = Rг + R1*m(1+n)/(1+m) = 706 Ом,

где m = R2/R1 = 10/15; n = R3/R10 = 1500/15 = 100.

Сопротивление R_Г можно определить, если в ветвь R1 ввести некоторую э.д.с. Е и определить ток Iг, который она вызывает в ветви Г указателя равновесия. Тогда R_1Г = E/Iг. Однако в данном случае R_1Г определить легче, если э.д.с. Е включить в ветвь указателя равновесия и найти ток I1, который она вызывает в ветви R1. В этом случае

R_1Г = E/I1; I1 =[E/(R_Г+Rг.вхо)]*[(R2+R4)/(R1+R2+R3+R4)].

Подставив в формулу для R_1Г соответствующие числовые значения, получим R_1Г.=(R_Г+Rг.вхо)(R1+R2+R3+R4)/(R2+R4)=Rг.г.(R1+R2+R3+R4)/(R2+R4) = 1765 Oм,

или R_1Г. = R_1Г.'(1+K_Г) = R1(1+n)(1+K_Г), где К_Г=R_Г/Rг.вхо=R_Г/(Rгг–R_Г);

К_Г=100/(706-100)= 0,165; R_1Г. = 15(1+100)(1+0,165) = 1765 Ом.

 

Пример 3.18. Каким должно быть критическое сопротивление Rкрит. гальванометра в схеме моста (рис.20), если Rп = 0, R1= 1 кОм, R2 =2 кОм, R3 = 1,5кОм, R4 = 3 кОм.

Решение.

Rкрит =Rг.вхо; Rг.вхо= (R1+R3)*(R2+R4)/(R1+R2+R3+R4) = 1667 Ом.

 

Пример 3.19. Мостовая цепь, показанная на рис.18 уравновешена. Определить Rх и Lх, если известно, что R2=5 Ом, L2=0,1 Г, R3=10 Ом, R4=20 Ом.

Решение.

Полагая Rх=R1; Lх=L1, а также учитывая, что Х3=Х4=0 из первого уравнения равновесия моста (3.24) находим:

R1*20–w*L1*0 = 5*10–w*0,1*0; Rх=R1=50/20=2,5 Ом.

Из второго уравнения (3.25) определяем L_Х

2,5*0+20*wL1 = 5*0+10* w *0,1; Lх=L₁=10*0,1*w / 20w= 0,05 Гн.

 

Пример 3.20. Мост, показанный на рис.19 уравновешен при следующих значениях параметров электрической цепи:R₂=2000 Ом; C₀=100 пФ; R4=10 кОм; C4=0,005 мкФ; d₃»tg d₃=0; d₄»tg d₄=0; f=50 Гц. Определить Rх, Cх и tg dх.

Решение.

Rx =(C4/C0)*R2 =0,005*10^-6*2000/(100*10^-12) = 100 кОм;

Cx = (R4/R2)*C0 = 10000*100*10^-12/2000 = 500 пФ;

tg dх = wCхRх = 2*3,14*50*500*10^-6*10⁵ = 0,005 рад.

 

Пример 3.21. Мост постоянного тока (рис.20) имеет параметры:R2=10 Ом; R3=1500 Ом; R4=1000 Ом; R_Г=100 Ом; Определить чувствительность моста по току Sоi, напряжению Sou и мощности Sow к изменению Ri, если Uп=4 В.

Решение.

Чувствительность по напряжению вблизи состояния равновесия определяется по формуле Sou = In*m*n/[(1+m)(1+n)]

In, m, n находятся по формулам:

In=Un/Rn.вхо=Un(R1+R2+R3+R4)/[(R1+R2)(R3+R4)]=Un(1+n)/R1(1+m)n;

m = R2/R1 = 10/16; n = R3/R1 = 1500/15 = 100.

Подставляя эти значения в формулу чувствительности, получим:

Sou=Un*m /[R1(1+m)²] = 4*10*15² /[15*15(15+10) ²] = 64*10^-3 В/Ом.

Чувствительность моста по напряжению к относительному изменению R_I равна:

S’ou = Sou*R₁₀ = 64*10^-3*15 = 0,96 B

Чувствительность по току

S_0I =Sou/(R_Г+Rг.вхо)= 64*10^-3/[100+(15+1500)(10+1000)/2525]=90*10^-6 A/Ом

Чувствительность по току к относительному изменению R_I

S’_0I = Sou/R_Г+Rг.вхо = 0,96/(100+606) = 13,6*10^-4 A.

Чувствительность моста по мощности к относительному изменению сопротивления вблизи состояния равновесия

S’ow = S’oi²*R_Г = 13,6²*10^-8 * 100 = 185*10^-6 Вт.

 

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: