 |
Пример использования метода Гаусса
|
|
|
|
Системы линейных уравнений
Основные понятия
К решению систем линейных уравнений сводятся многочисленные практические задачи [8, 17, 18]. Можно утверждать, что решение линейных уравнений является одной из самых распространенных и важных задач вычислительной математики (численных методов).
Запишем систему из n линейных алгебраических уравнений с n неизвестными:
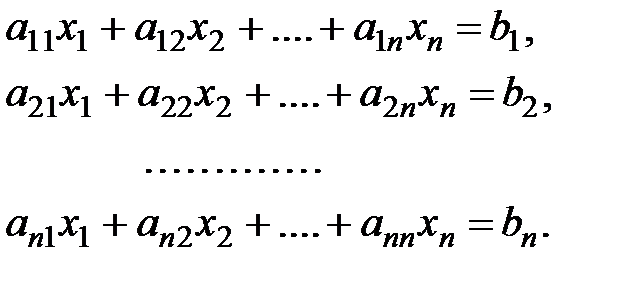(3.1)
Коэффициенты этой системы образуют квадратную матрицу
. (3.2)
Введем обозначения: Х - вектор-столбец неизвестных х i; В - вектор-столбец свободных членов системы (3.1) b i (i = 1, 2, …, n). Тогда
(3.3)
Система уравнений (3.1) в матричном виде:
А*Х=В. (3.4)
Определителем матрицы А называется число D, равное:
(3.5)
Необходимым и достаточным условием существования единственного
решения системы линейных уравнений является условие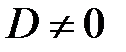 
.
Методы решения систем линейных уравнений делятся на прямые и итерационные [7, 13, 14]. Прямые методы используют конечные формулы для вычисления неизвестных. Причем формулы применяют однократно без повторов с целью уточнения неизвестных. Точность решения зависит от количества знаков, сохраняемых в дробной части чисел на каждом этапе вычислений. Прямые методы дают решение после выполнения заранее известного количества операций. Эти методы сравнительно просты и универсальны. Одним из прямых методов является метод Крамера (метод определителей). Приведем метод для решения системы из трех уравнений:
|
|
|
(3.6)
Корни системы уравнений
, 
, 
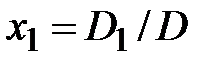, (3.6)
где определители 
, 
, 
, 
вычисляют по формулам:
= (3.7)
= 
,
, 
, 
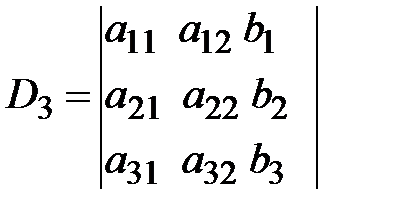. (3.8)
При решении системы уравнений на рабочем листе Excel для вычисления определителей следует использовать стандартную математическую функцию МОПРЕД. Например, если матрица размерностью 3х3 записана в ячейках B 2: D 4, то формула для вычисления определителя в Excel имеет вид:
= МОПРЕД (B 2: D 4)
Следует отметить, что прямые методы имеют ряд недостатков. Наиболее
существенным является накапливание погрешностей в процессе решения, так как вычисления на любом этапе используют результаты всех предыдущих операций. Погрешности накапливаются из-за отбрасывания в ЭВМ младших разрядов чисел. Это особо опасно для больших систем (n > 200), а так же для плохо обусловленных систем (определитель D близок к нулю). Прямые методы не используют так же для систем с плохо заполненной матрицей (содержащей много нулей).
Итерационные методы – это методы последовательных приближений. В них необходимо задать некоторое приближенное решение – начальное приближение. После этого по определенному алгоритму проводится один цикл вычислений, называемый итерацией. В результате итерации находят новое приближение. Итерации проводятся до получения решения с заданной точностью. Алгоритмы решения систем линейных уравнений с использованием итерационных методов обычно более сложные по сравнению с прямыми методами. Объем вычислений заранее определить трудно.
Однако итерационные методы в ряде случаев предпочтительнее. Например, погрешности окончательных результатов при их использовании не накапливаются, так как точность вычислений в каждой итерации определяется лишь результатами предыдущей итерации и практически не зависит от ранее выполненных вычислений. Для реализации итерационных методов часто требуется меньше памяти компьютера по сравнению с использованием прямых методов.
|
|
|
Эти достоинства итерационных методов делают их полезными в случае большого числа уравнений, а также плохо обусловленных систем.
Метод Гаусса
Наиболее распространенным среди прямых методов решения систем линейных уравнений является метод исключения Гаусса и его модификации [18, 19]. Он основан на приведении матрицы системы к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений системы. Сначала с помощью первого уравнения исключается x 1 из второго и всех последующих уравнений системы. Затем с помощью второго уравнения исключается x 2 из третьего и всех последующих уравнений. Этот процесс называется прямым ходом метода Гаусса. Он продолжается до тех пор, пока в левой части последнего n -го уравнения не останется лишь один член с неизвестным x n. Таким образом, матрица системы будет приведена к треугольному виду.
Обратный ход метода Гаусса состоит в последовательном вычислении искомых неизвестных: решая последнее уравнение, находим единственное неизвестное x n. Далее, используя это значение из предыдущего уравнения, вычисляем x n-1 и т.д. Последним находим x 1 из первого уравнения.
Рассмотрим применение метода Гаусса для системы из трех уравнений:
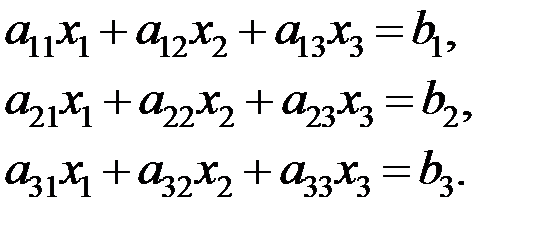(3.9)
Для исключения x 1 из второго уравнения прибавим к нему первое, умноженное на 
. Затем умножим первое уравнение на 
и прибавим результат к третьему. Из третьего так же исключится x 1. Получим равносильную систему вида:
(3.10)
где 
, (i, j = 2, 3), 
, (i = 2, 3).
Например: 
, 
.
Теперь из третьего уравнения системы (3.10) надо исключить x 2. Для этого второе уравнение умножим на 
и прибавим результат к третьему.
Получим:
(3.11)
где 
, 
.
Матрица системы (3.11) имеет треугольный вид. На этом заканчивается прямой ход метода Гаусса.
|
|
|
Заметим, что в процессе исключения неизвестных приходится выполнять операции деления на коэффициенты a 11, a 22 и т.д. Поэтому они должны быть отличными от нуля. В противном случае необходимо соответствующим образом переставить уравнения системы.
Обратный ход начинается с решения третьего уравнения системы (3.11):
.
Используя это значение можно найти x 2из второго уравнения, а затем x 1 из первого:
,
.
Аналогично строится вычислительный алгоритм для линейной системы с произвольным числом уравнений.
Программы для решения систем линейных уравнений методом Гаусса будут представлены далее в разделах 4.6.2 и 5.7.
Пример использования метода Гаусса
Решим систему уравнений:
(3.12)
Исключим x 1 из второго и третьего уравнений. Для этого сначала умножим первое уравнение на 0,3 и результат прибавим ко второму. Затем умножим первое же уравнение на -0,5 и результат прибавим к третьему. Получим:
(3.13)
В системе (3.13) умножим второе уравнение на 25 и результат сложим с третьим уравнением. Получим систему в треугольном виде:
(3.14)
На этом заканчивается прямой ход метода Гаусса. Обратный ход состоит в последовательности вычислении x 3, x 2, x 1 соответственно из третьего, второго и первого уравнений:
.
Метод Зейделя
Метод является одним из самых распространенных итерационных методов решения систем линейных уравнений [8, 13]. Метод рассмотрим на примере решения системы из трех уравнений:
(3.15)
Предположим, что диагональные элементы a 11, a 22, a 33отличны от нуля. В противном случае нужно переставить уравнения. Выразим неизвестные x 1, x 2, x 3 соответственно из первого, второго и третьего уравнений системы (3.15):
|
|
|
, (3.16)
, (3.17)
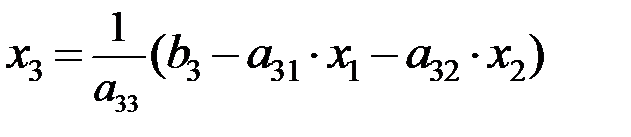. (3.18)
Зададим некоторые начальные (нулевые) приближения значений неизвестных:
.
Подставляя эти значения в правую часть выражения (3.16), получим новое (первое) приближение для x 1:
.
Используя значение x 1 = 
и приближение x 3(0), находим из (3.17) первое приближение для x 2:
.
И, наконец, используя вычисленные значения x 1 = x 1(1) и x 2 = x 2(1), находим с помощью выражения (3.18) первое приближение для x 3:
.
На этом заканчивается первая итерация решения системы (3.16), (3.17), (3.18). Используя теперь значения x 1(1 ) , x 2(1), x 3(1), можно таким же способом провести вторую итерацию. В результате нее будут найдены вторые приближения к решению: x 1 = x 1(2 ) , x 2 = x 2(2), x 3 = x 3(2). Затем выполняется третья и последующие итерации. Приближение с номером k можно представить в виде:
(3.19)
Итерационный процесс продолжается до тех пор, пока значения x 1(k), x 2(k), x 3(k) не станут близкими с заданной погрешностью к значениям x 1(k-1), x 2(k-1), x 3(k-1). Т.е. вычисляется параметр
.
Если
δ < ε, (3.20)
то процесс прекращается. Величина погрешности вычислений ε > 0. Это малое, заданное в исходных данных число. Обычно ε = 10-2…10-6.
Во избежание непроизводительных затрат компьютерного времени в алгоритм можно ввести счетчик числа итераций. Если процесс сходится, то вычисления прекращаются при выполнении условия (3.20). Если не сходится, то вычисления прекращаются при достижении числа итераций k некоторого заданного значения M. Число M достаточно большое: M ≥ 100.
Отметим, что для того, чтобы процесс итерационных вычислений сошелся (если он не сходится), можно поменять начальные приближения x i(0).
Блок – схема алгоритма метода Зейделя аналогична другим итерационным методам (рис. 3.1). После выбора начальных приближений x i(0) организуется циклический вычислительный процесс, каждый цикл которого представляет собой одну итерацию. В результате каждой итерации получаются новые значения неизвестных. При малом изменении этих значений на двух последовательных итерациях вычисления прекращаются. Происходит вывод значений неизвестных, полученных на последней итерации.
|
|
|
