 |
Случайных процессов и математической статистики
|
|
|
|
Контрольная работа № 2
| Вариант 0 | |||||||||||||||
| Среди 25 студентов, где 10 девушек, разыгрываются 5 билетов в кино. Определить вероятность того, что среди обладателей билетов окажутся 1) две девушки, 2) хотя бы одна девушка. | |||||||||||||||
| Вероятности успешной сдачи экзамена по первому, второму и третьему предметам у данного студента соответственно равны 0,6; 0,7 и 0,75. Найти вероятность того, что он успешно сдаст все экзамены. | |||||||||||||||
| Вероятность попадания в десятку у данного стрелка при одном выстреле равна 0,2. Определить вероятность попадания в десятку не менее трёх раз при 5 выстрелах. | |||||||||||||||
СВ Найти: 1) числовые характеристики 2) функцию распределения 3) вероятность 4) закон распределения величины СВ 5) | |||||||||||||||
На пути движения автомобиля 4 светофоров, каждый из них разрешает дальнейшее движение с вероятностью 0,6.
Составьте закон распределения СВ  , равной числу светофоров, пройденных автомобилем до первой остановки, и постройте многоугольник распределения.
Найдите математическое ожидание , равной числу светофоров, пройденных автомобилем до первой остановки, и постройте многоугольник распределения.
Найдите математическое ожидание 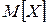 и дисперсию и дисперсию  этой СВ.
Найдите вероятности событий: а) А – автомобиль проедет хотя бы два светофора; б) В – автомобиль проедет не менее трех светофоров. этой СВ.
Найдите вероятности событий: а) А – автомобиль проедет хотя бы два светофора; б) В – автомобиль проедет не менее трех светофоров.
| |||||||||||||||
Дана плотность вероятности  непрерывной СВ X: непрерывной СВ X:
 Найти:
1) параметр С и построить график
Найти:
1) параметр С и построить график  ;
2) интегральную функцию F (x)и построить ее график;
3) математическое ожидание mX, дисперсию DX и среднее квадратическое отклонение s (x);
4) вероятность Р(0,5< X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. ;
2) интегральную функцию F (x)и построить ее график;
3) математическое ожидание mX, дисперсию DX и среднее квадратическое отклонение s (x);
4) вероятность Р(0,5< X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
| |||||||||||||||
Заданы математическое ожидание  и среднее квадратичное отклонение и среднее квадратичное отклонение  нормально распределенной непрерывной СВ. Известны: нормально распределенной непрерывной СВ. Известны: 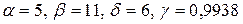 .
Найти:
1) вероятность .
Найти:
1) вероятность  ;
2) вероятность ;
2) вероятность  ;
3) симметричный, относительно ;
3) симметричный, относительно  , интервал, в который попадает величина , интервал, в который попадает величина  с вероятностью с вероятностью  ;
4) интервал, в котором практически окажутся все значения величины ;
4) интервал, в котором практически окажутся все значения величины  .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту. .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту.
| |||||||||||||||
Дано распределение выборочной совокупности:
1. Построить полигон, гистограмму и кумуляту относительных частот.
2. Найти числовые характеристики выборочной совокупности: | |||||||||||||||
| Вариант 1 | |||||||||||||||
| В 25 экзаменационных билетах содержатся по три вопроса, которые не повторяются. Студент знает ответы на 45 вопросов. Какова вероятность того, что 1) доставшийся билет состоит из подготовленных им вопросов, 2) хотя бы один вопрос подготовлен? | |||||||||||||||
| Студент пришел на зачёт, зная из 30 вопросов программы только 24. Чему равна вероятность сдать зачёт, если для этого надо ответить на случайно доставшийся ему вопрос, а в случае неудачи ответить на дополнительный вопрос, предложенный ему преподавателем случайным образом? | |||||||||||||||
| Игрок набрасывает кольца на колышек, вероятность удачи при этом равна 0,1. Найти вероятность того, что из шести колец на колышек попадут хотя бы два. | |||||||||||||||
СВ Найти: 1) числовые характеристики 2) функцию распределения 3) вероятность 4) закон распределения величины СВ 5) | |||||||||||||||
Из 25 контрольных работ, среди которых 5 оценены на отлично, наугад извлекаются 3 работы.
Составьте закон распределения дискретной СВ  , равной числу оцененных на "отлично" работ среди извлеченных, и постройте многоугольник распределения.
Найдите математическое ожидание , равной числу оцененных на "отлично" работ среди извлеченных, и постройте многоугольник распределения.
Найдите математическое ожидание 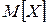 и дисперсию и дисперсию  этой СВ.
Найдите вероятности событий: а) А – извлекут хотя бы две отличных работы; б) В – будет не более одной отличной работы. этой СВ.
Найдите вероятности событий: а) А – извлекут хотя бы две отличных работы; б) В – будет не более одной отличной работы.
| |||||||||||||||
Дана плотность вероятности  непрерывной СВ X: непрерывной СВ X:
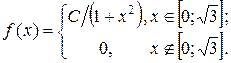 Найти:
1) параметр С и построить график
Найти:
1) параметр С и построить график  ;
2) интегральную функцию F (x)и построить ее график;
3) математическое ожидание mX, дисперсию DX и среднее квадратическое отклонение s (x);
4) вероятность Р(X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. ;
2) интегральную функцию F (x)и построить ее график;
3) математическое ожидание mX, дисперсию DX и среднее квадратическое отклонение s (x);
4) вероятность Р(X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
| |||||||||||||||
Заданы математическое ожидание  и среднее квадратичное отклонение и среднее квадратичное отклонение  нормально распределенной непрерывной СВ. Известны: нормально распределенной непрерывной СВ. Известны:  .
Найти:
1) вероятность .
Найти:
1) вероятность  ;
2) вероятность ;
2) вероятность  ;
3) симметричный, относительно ;
3) симметричный, относительно  , интервал, в который попадает величина , интервал, в который попадает величина  с вероятностью с вероятностью  ;
4) интервал, в котором практически окажутся все значения величины ;
4) интервал, в котором практически окажутся все значения величины  .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту. .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту.
| |||||||||||||||
Дано распределение выборочной совокупности:
1. Построить полигон, гистограмму и кумуляту относительных частот.
2. Найти числовые характеристики выборочной совокупности: | |||||||||||||||
| Вариант 2 | |||||||||||||||
| Из партии, состоящей из 20 радиоприемников, для проверки произвольно отбирают три приемника. Партия содержит пять неисправных приемников. Какова вероятность того, что в число отобранных войдут 1) один неисправный и два исправных радиоприемника; 2) хотя бы один исправный радиоприемник? | |||||||||||||||
| Для сигнализации о возгорании установлены два независимо работающих датчика. Вероятности того, что при возгорании датчик сработает, для первого и второго датчиков соответственно равны 0,9 и 0,95. Найти вероятность того, что при пожаре сработает хотя бы один датчик. | |||||||||||||||
| В магазин вошли восемь покупателей. Найти вероятность того, что трое из них совершат покупки, если вероятность совершить покупку для каждого равна 0,3. | |||||||||||||||
СВ Найти: 1) числовые характеристики
2) функцию распределения 3) вероятность 4) закон распределения величины СВ 5) | |||||||||||||||
По каналу связи передаются два сообщения, каждое из которых может быть искажено. Вероятности искажения 1-го и 2-го сообщения соответственно равны 0,2 и 0,1. СВ  – число правильно переданных сообщений.
Составьте закон распределения и постройте многоугольник полученного распределения.
Найдите математическое ожидание – число правильно переданных сообщений.
Составьте закон распределения и постройте многоугольник полученного распределения.
Найдите математическое ожидание 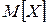 и дисперсию и дисперсию  .
Найдите вероятности событий: а) А – передано не более одного правильного сообщения; б) В – хотя бы одно сообщение передано правильно. .
Найдите вероятности событий: а) А – передано не более одного правильного сообщения; б) В – хотя бы одно сообщение передано правильно.
| |||||||||||||||
Дана плотность вероятности  непрерывной СВ X: непрерывной СВ X:
 Найти:
1) параметр С и построить график
Найти:
1) параметр С и построить график  ;
2) интегральную функцию F (x)и построить ее график;
3) математическое ожидание mX, дисперсию DX и среднее квадратическое отклонение s (x);
4) вероятность Р(X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. ;
2) интегральную функцию F (x)и построить ее график;
3) математическое ожидание mX, дисперсию DX и среднее квадратическое отклонение s (x);
4) вероятность Р(X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
| |||||||||||||||
Заданы математическое ожидание  и среднее квадратичное отклонение и среднее квадратичное отклонение  нормально распределенной непрерывной СВ. Известны: нормально распределенной непрерывной СВ. Известны:  .
Найти:
1) вероятность .
Найти:
1) вероятность  ;
2) вероятность ;
2) вероятность  ;
3) симметричный, относительно ;
3) симметричный, относительно  , интервал, в который попадает величина , интервал, в который попадает величина  с вероятностью с вероятностью  ;
4) интервал, в котором практически окажутся все значения величины ;
4) интервал, в котором практически окажутся все значения величины  .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту. .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту.
| |||||||||||||||
Дано распределение выборочной совокупности:
1. Построить полигон, гистограмму и кумуляту относительных частот. 2. Найти числовые характеристики выборочной совокупности: | |||||||||||||||
| Вариант 3 | |||||||||||||||
| В партии из 15 деталей имеются 4 бракованных. Какова вероятность того, что среди наудачу отобранных 5 деталей окажутся 1) две бракованными; 2) хотя бы одна бракованная? | |||||||||||||||
| Вероятность попадания в мишень при одном выстреле равна 0,6. По мишени стреляют одиночными выстрелами до первого попадания, после чего стрельбу прекращают. Найти вероятность того, что будет сделано не более трех выстрелов. | |||||||||||||||
| При передаче сообщения вероятность искажения одного знака равна 0,01. Определить вероятность того, что сообщение из 10 знаков содержит ровно три искажения. | |||||||||||||||
СВ
Найти: 1) числовые характеристики 2) функцию распределения 3) вероятность 4) закон распределения величины СВ 5) | |||||||||||||||
Радиостанция через определенные промежутки времени посылает позывные сигналы (не более четырех) до установления двусторонней связи. Вероятность получения ответа на позывной сигнал равна 0,3.
Составьте закон распределения СВ  – числа посланных позывных и постройте многоугольник распределения.
Найдите математическое ожидание – числа посланных позывных и постройте многоугольник распределения.
Найдите математическое ожидание 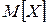 и дисперсию и дисперсию  этой СВ.
Найдите вероятности событий: а) А – связь установится с третьего сигнала; б) В – будет не более двух позывных. этой СВ.
Найдите вероятности событий: а) А – связь установится с третьего сигнала; б) В – будет не более двух позывных.
| |||||||||||||||
Дана плотность вероятности  непрерывной СВ X: непрерывной СВ X:
 Найти:
1) параметр С и построить график
Найти:
1) параметр С и построить график  ;
2) интегральную функцию F (x)и построить ее график;
3) математическое ожидание mX, дисперсию DX и среднее квадратическое отклонение s (x);
4) вероятность Р(X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. ;
2) интегральную функцию F (x)и построить ее график;
3) математическое ожидание mX, дисперсию DX и среднее квадратическое отклонение s (x);
4) вероятность Р(X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
| |||||||||||||||
Заданы математическое ожидание  и среднее квадратичное отклонение и среднее квадратичное отклонение  нормально распределенной непрерывной СВ. Известны: нормально распределенной непрерывной СВ. Известны: 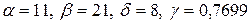 .
Найти:
1) вероятность .
Найти:
1) вероятность  ;
2) вероятность ;
2) вероятность  ;
3) симметричный, относительно ;
3) симметричный, относительно  , интервал, в который попадает величина , интервал, в который попадает величина  с вероятностью с вероятностью  ;
4) интервал, в котором практически окажутся все значения величины ;
4) интервал, в котором практически окажутся все значения величины  .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту. .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту.
| |||||||||||||||
Дано распределение выборочной совокупности:
1. Построить полигон, гистограмму и кумуляту относительных частот. 2. Найти числовые характеристики выборочной совокупности: | |||||||||||||||
| Вариант 4 | |||||||||||||||
| Из партии, в которой 30 микросхем без дефекта и 5 с дефектами, берут наудачу 3 микросхемы. Найти вероятность того, что 1) две микросхемы без дефекта; 2) по крайней мере одна микросхема без дефекта. | |||||||||||||||
| В магазин от разных поставщиков поступают 4 партии различных видов мебели, из которых комплектуются гарнитуры. Вероятности того, что партии товара будут доставлены в срок, равны соответственно 0,9; 0,8; 0,7 и 0,95. Найти вероятность того, что хотя бы одна партия не будет доставлена в срок. | |||||||||||||||
| Для данного баскетболиста вероятность забросить мяч в корзину равна 0,7. Проведено 10 бросков. Что вероятнее: он забросит мяч в корзину 6 или 8 раз? | |||||||||||||||
СВ
Найти: 1) числовые характеристики 2) функцию распределения 3) вероятность 4) закон распределения величины СВ 5) | |||||||||||||||
В коробке имеются 7 карандашей, из которых – 4 красные. Из этой коробки наудачу извлекаются 3 карандаша.
Составьте закон распределения СВ  , равной числу красных карандашей в выборке, и постройте многоугольник распределения.
Найдите математическое ожидание , равной числу красных карандашей в выборке, и постройте многоугольник распределения.
Найдите математическое ожидание 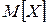 и дисперсию и дисперсию  этой СВ.
Найдите вероятность события: а) А – выбрали не менее двух красных карандашей; б) В – выбрали хотя бы один красный карандаш. этой СВ.
Найдите вероятность события: а) А – выбрали не менее двух красных карандашей; б) В – выбрали хотя бы один красный карандаш.
| |||||||||||||||
Дана плотность вероятности  непрерывной СВ X: непрерывной СВ X:
 Найти:
1) параметр С и построить график
Найти:
1) параметр С и построить график  ;
2) интегральную функцию F (x)и построить ее график;
3) математическое ожидание mX, дисперсию DX и среднее квадратическое отклонение s (x);
4) вероятность Р(X > 1) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. ;
2) интегральную функцию F (x)и построить ее график;
3) математическое ожидание mX, дисперсию DX и среднее квадратическое отклонение s (x);
4) вероятность Р(X > 1) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
| |||||||||||||||
Заданы математическое ожидание 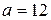 и среднее квадратичное отклонение и среднее квадратичное отклонение 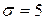 нормально распределенной непрерывной СВ. Известны: нормально распределенной непрерывной СВ. Известны:  .
Найти:
1) вероятность .
Найти:
1) вероятность  ;
2) вероятность ;
2) вероятность  ;
3) симметричный, относительно ;
3) симметричный, относительно  , интервал, в который попадает величина , интервал, в который попадает величина  с вероятностью с вероятностью  ;
4) интервал, в котором практически окажутся все значения величины ;
4) интервал, в котором практически окажутся все значения величины  .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту. .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту.
| |||||||||||||||
Дано распределение выборочной совокупности:
1. Построить полигон, гистограмму и кумуляту относительных частот. 2. Найти числовые характеристики выборочной совокупности: | |||||||||||||||
| Вариант 5 | |||||||||||||||
| В новогодней лотерее 25 билетов, 10 из которых выигрывают. Гражданин купил 4 билетов. Какова вероятность того, что 1) три будут выигрышными; 2) по крайне мере один из купленных билетов выигрышный? | |||||||||||||||
| Для разрушения моста достаточно одного попадания из орудия. Найти вероятность разрушения моста, если из орудия сделано 4 выстрела и вероятность попадания при первом выстреле равна 0,3, при втором - 0,4, третьем - 0,5 и четвёртом - 0,7. | |||||||||||||||
| Два равносильных игрока играют в шахматы (ничьи не учитываются). Что вероятнее: первый игрок выиграет 3 партии из 6, или 4 партии из 8? | |||||||||||||||
СВ Найти: 1) числовые характеристики 2) функцию распределения 3) вероятность 4) закон распределения величины СВ 5) | |||||||||||||||
Дважды брошена игральная кость. СВ  равна сумме очков при двух бросках.
Составьте закон распределения равна сумме очков при двух бросках.
Составьте закон распределения  и постройте многоугольник распределения.
Найдите математическое ожидание и постройте многоугольник распределения.
Найдите математическое ожидание 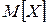 и дисперсию и дисперсию  СВ.
Найдите вероятности событий: а) А – сумма очков будет менее двух; б) В – сумма очков будет более пяти. СВ.
Найдите вероятности событий: а) А – сумма очков будет менее двух; б) В – сумма очков будет более пяти.
| |||||||||||||||
Дана плотность вероятности  непрерывной СВ X: непрерывной СВ X:
 Найти:
1) параметр С и построить график
Найти:
1) параметр С и построить график  ;
2) интегральную функцию F (x)и построить ее график;
3) математическое ожидание mX, дисперсию DX и среднее квадратическое отклонение s (x);
4) вероятность Р(X >1,5) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. ;
2) интегральную функцию F (x)и построить ее график;
3) математическое ожидание mX, дисперсию DX и среднее квадратическое отклонение s (x);
4) вероятность Р(X >1,5) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
| |||||||||||||||
Заданы математическое ожидание  и среднее квадратичное отклонение и среднее квадратичное отклонение  нормально распределенной непрерывной СВ. Известны: нормально распределенной непрерывной СВ. Известны:  .
Найти:
1) вероятность .
Найти:
1) вероятность  ;
2) вероятность ;
2) вероятность  ;
3) симметричный, относительно ;
3) симметричный, относительно  , интервал, в который попадает величина , интервал, в который попадает величина  с вероятностью с вероятностью  ;
4) интервал, в котором практически окажутся все значения величины ;
4) интервал, в котором практически окажутся все значения величины  .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту. .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту.
| |||||||||||||||
Дано распределение выборочной совокупности:
1. Построить полигон, гистограмму и кумуляту относительных частот. 2. Найти числовые характеристики выборочной совокупности: | |||||||||||||||
| Вариант 6 | |||||||||||||||
| В оперотряде 10 человек, среди них 7 мужчин. На исследование места аварии направляется группа из 6 человек. Найти вероятность того, что в группе будет: 1) 4 мужчины; 2) хотя бы одна женщина? | |||||||||||||||
| Три орудия ведут огонь по цели, вероятность попадания в которую при одном выстреле из первого орудия – 0,5, из второго – 0,6, из третьего – 0,7. Зная, что каждое орудие стреляет один раз, найти вероятность поражения цели, если для этого достаточно двух попаданий. | |||||||||||||||
| В квартире 4 электролампочки. Для каждой лампочки вероятность того, что она остается исправной в течении года, равна 5/6.Какова вероятность того, что в течении года придется заменить не меньше половины лампочек? | |||||||||||||||
СВ Найти: 1) числовые характеристики 2) функцию распределения 3) вероятность 4) закон распределения величины СВ 5) | |||||||||||||||
Два стрелка делают по одному выстрелу по мишени. Вероятность попадания для 1-го стрелка – 0,4, для 2-го – 0,7. СВ  – сумма числа попаданий двумя стрелками.
Составьте закон распределения – сумма числа попаданий двумя стрелками.
Составьте закон распределения  и постройте многоугольник распределения, найдите математическое ожидание и постройте многоугольник распределения, найдите математическое ожидание 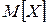 и дисперсию и дисперсию  этой СВ.
Найдите вероятности событий: а) А – сумма очков не менее 2; б) В – сумма очков более одного. этой СВ.
Найдите вероятности событий: а) А – сумма очков не менее 2; б) В – сумма очков более одного.
| |||||||||||||||
Дана плотность вероятности  непрерывной СВ X: непрерывной СВ X:
 Найти:
1) параметр С и построить график
Найти:
1) параметр С и построить график  ;
2) интегральную функцию F (x)и построить ее график;
3) математическое ожидание mX, дисперсию DX и среднее квадратическое отклонение s (x);
4) вероятность Р(0,5< X <2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. ;
2) интегральную функцию F (x)и построить ее график;
3) математическое ожидание mX, дисперсию DX и среднее квадратическое отклонение s (x);
4) вероятность Р(0,5< X <2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
| |||||||||||||||
Заданы математическое ожидание  и среднее квадратичное отклонение и среднее квадратичное отклонение  нормально распределенной непрерывной СВ. Известны: нормально распределенной непрерывной СВ. Известны:  .
Найти:
1) вероятность .
Найти:
1) вероятность  ;
2) вероятность ;
2) вероятность  ;
3) симметричный, относительно ;
3) симметричный, относительно  , интервал, в который попадает величина , интервал, в который попадает величина  с вероятностью с вероятностью  ;
4) интервал, в котором практически окажутся все значения величины ;
4) интервал, в котором практически окажутся все значения величины  .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту. .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту.
| |||||||||||||||
Дано распределение выборочной совокупности:
1. Построить полигон, гистограмму и кумуляту относительных частот. 2. Найти числовые характеристики выборочной совокупности: | |||||||||||||||
| Вариант 7 | |||||||||||||||
| В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов для проверки остаточных знаний. Найти вероятность того, что среди отобранных студентов: 1) 5 отличников; 2) хотя бы один не отличник. | |||||||||||||||
| Из колоды в 32 карты наугад одна за другой вынимаются две карты. Найти вероятность того, что вынут валет и дама. | |||||||||||||||
| Всхожесть семян данного сорта растений оценивается с вероятностью, равной 0,8. Какова вероятность того, что из пяти посеянных семян взойдут не менее трех? | |||||||||||||||
СВ Найти: 1) числовые характеристики 2) функцию распределения 3) вероятность 4) закон распределения величины СВ 5) | |||||||||||||||
С вероятностью попадания при одном выстреле 0,7 охотник стреляет по дичи до первого попадания, но успевает сделать не более 4 выстрелов. Дискретная СВ  – число выстрелов.
Составьте закон распределения – число выстрелов.
Составьте закон распределения 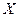 и постройте многоугольник распределения.
Найдите математическое ожидание и постройте многоугольник распределения.
Найдите математическое ожидание 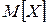 и дисперсию и дисперсию  этой СВ.
Найдите вероятности событий: а) А – сделано не менее двух выстрелов; б) В – хотя бы три выстрела. этой СВ.
Найдите вероятности событий: а) А – сделано не менее двух выстрелов; б) В – хотя бы три выстрела.
| |||||||||||||||
Дана плотность вероятности  непрерывной СВ X: непрерывной СВ X:
 Найти:
1) параметр С и построить график
Найти:
1) параметр С и построить график  ;
2) интегральную функцию F (x)и построить ее график;
3) математическое ожидание mX, дисперсию DX и среднее квадратическое отклонение s (x);
4) вероятность Р(X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. ;
2) интегральную функцию F (x)и построить ее график;
3) математическое ожидание mX, дисперсию DX и среднее квадратическое отклонение s (x);
4) вероятность Р(X < 2) дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
| |||||||||||||||
Заданы математическое ожидание  и среднее квадратичное отклонение и среднее квадратичное отклонение  нормально распределенной непрерывной СВ. Известны: нормально распределенной непрерывной СВ. Известны:  .
Найти:
1) вероятность .
Найти:
1) вероятность  ;
2) вероятность ;
2) вероятность  ;
3) симметричный, относительно ;
3) симметричный, относительно  , интервал, в который попадает величина , интервал, в который попадает величина  с вероятностью с вероятностью  ;
4) интервал, в котором практически окажутся все значения величины ;
4) интервал, в котором практически окажутся все значения величины  .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту. .
Дайте графические пояснения ответов на кривой нормального распределения к каждому пункту.
| |||||||||||||||
Дано распределение выборочной совокупности:
1. Построить полигон, гистограмму и кумуляту относительных частот. 2. Найти числовые характеристики выборочной совокупности: | |||||||||||||||
| Вариант 8 | |||||||||||||||
| В ящике 5 новых и 7 старых инструментов. Рабочему выдали 3 инструмента. Найти вероятность того, что: 1) два из трех выданных инструментов старые; 2) хотя бы один из трех инструментов новый. | |||||||||||||||
| Из пяти карточек с буквами А, Б, В, Г, Д наугад одна за другой выбираются три и располагаются в ряд в порядке появления. Какова вероятность того, что получится слово “два”? | |||||||||||||||
| Какова вероятность того, что при 8 бросаниях монеты герб выпадет 5 раз? | |||||||||||||||
СВ Найти: 1) числовые характеристики 2) функцию распределения 3) вероятность 4) закон распределения величины СВ 5) | |||||||||||||||
Два стрелка стреляют по одной мишени, делая по 2 выстрела. Вероятность попадания для первого стрелка равна 0,5, для второго – 0,6.
Составьте закон распределения СВ  , равной произведению числа попаданий, и постройте многоугольник распределения.
Найдите математическое ожидание , равной произведению числа попаданий, и постройте многоугольник распределения.
Найдите математическое ожидание 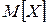 и дисперсию и дисперсию  этой СВ.
Найдите вероятности событий: а) А – произведение очков не более одного; б) В – произведение очков более трёх. этой СВ.
Найдите вероятности событий: а) А – произведение очков не более одного; б) В – произведение очков более трёх.
| |||||||||||||||
Дана плотность вероятности  непрерывной СВ X: непрерывной СВ X:
 Найти:
1) параметр С и построить график
Найти:
1) параметр С и построить график  ;
2) интегральную функцию F (x)и построить ее график;
3) математ ;
2) интегральную функцию F (x)и построить ее график;
3) математ
Воспользуйтесь поиском по сайту:  ©2015 - 2026 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...
|




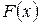 и построить ее график;
и построить ее график; ;
; .
. ,
,  дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.

 ,
,  , s.
, s. .
. .
. .
. .
. .
. .
. .
. .
.