 |
Построение изображения в фотокамере.
|
|
|
|
Для фотограмметрической съемки местности или исследуемых объектов применяются оптические системы – фотокамеры. Их очень часто называют метрическими камерами, так как по полученным с их помощью снимкам можно определять фотокоординаты изобразившихся на них точек (предусмотрена возможность введения системы прямоугольных координат в плоскости снимка). При этом искажение изображения на снимке сведено к минимуму. Обычные любительские фотоаппараты такими свойствами не обладают, так как для них главное - художественное качество полученных при фотографировании изображений.
Фотокамеры, используемые для фотографирования местности с летательного аппарата, называются аэрофотоаппаратами (или АФА) а, для фотографирования ее с точек земной поверхности - фототеодолитами.
Изображение в фотокамере строится на плоскости (пленке или пластинке со светочувствительным слоем, или ПЗС матрице) с помощью объектива, представляющего собой сложную оптическую систему собирательных и рассеивающих линз, центры кривизны сферических поверхностей которых расположены на одной прямой линии, называемой главной оптической осью.
Рассмотрим особенности построения изображения объекта идеальным объективом. Они основаны на следующих законах геометрической оптики:
- прямолинейности распространения световых лучей в однородной среде;
- независимости распространения отдельных световых лучей и пучков;
- обратимости лучей света;
- отражении и преломлении световых лучей на границе двух сред.
Законы геометрической оптики позволяют сложную оптическую систему идеального объектива заменить упрощенной моделью (линзой), сечение которой плоскостью, проходящей через главную оптическую ось, показано на рис. 1.
|
|
|
На нем: R 1 и R 2 – передняя и задняя поверхности объектива; S 1 и S 2 – его передняя и задняя узловые точки; F 1 и F 2 – передний и задний главные фокусы; H 1 и H 2 – главные плоскости объектива (они проходят через точки S 1 и S 2 перпендикулярно главной оптической оси).
Передняя узловая точка S 1 относится к пространству предметов местности и является точкой фотографирования. Задняя узловая точка S 2 относится к пространству изображения и является центром проекции. Узловые точки обладают тем свойством, что любой луч, вошедший в переднюю узловую точку, выйдя из задней узловой точки, не меняет направления. Такие лучи называются центральными.
Главным фокусом объектива (линзы) называется точка схода лучей идущих от бесконечно удаленного предмета, параллельно главной оптической оси. Их два. Плоскости, проходящие через главные фокусы перпендикулярно к главной оптической оси, называются фокальными плоскостями.
 |
Изображение любой точки, например, А, фотографируемого объекта местности строится следующим образом. Луч идущий параллельно главной оптической оси, преломляется на главной задней плоскости H 2 и проходит через задний фокус F 2. Луч, проходящий через передний фокус F 1, после преломления на передней главной плоскости H 1 пойдет параллельно оптической оси. В соответствии с законами геометрической оптики центральный луч AS входит в переднюю узловую точку S 1 под углом b к оптической оси и выходит из задней узловой точки S 2 под тем же углом к ней. В результате таких построений все три луча пересекутся в точке a на плоскости P 1. При этом для точек A и a будет выполняться условие оптического сопряжения
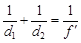
| (1) |
где d 1 – расстояние от плоскости H 2 до плоскости изображения P 1; d 2 – расстояние от плоскости H 1 до точки фотографируемого объекта; f¢ – фокусное расстояние объектива (рис. 1).
|
|
|
Говорят, что объектив, изображенный на рисунке строит действительное, уменьшенное и перевернутое (обратное) изображение рассматриваемого объекта.
Для точки расположенной ближе или дальше (т.е. d2 другое), условие (1) не выполняется, поэтому ее изображение в плоскости P 1 будет иметь вид размытого кружка. Но если его диаметр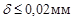 
, глаз воспринимает изображение как четкую точку.
При фотографировании в целях картографирования, когда расстояние d 1 значительно меньше расстояния d 2 (то есть можно считать, что d 2 равно бесконечности) d 1= f¢, все точки фотографируемого объекта достаточно резко изображаются на плоскости P 2 (главной фокальной плоскости), которая расположена перпендикулярно оптической оси и проходит через главный задний фокус F 2. По этой причине в АФА и фототеодолитах плоскость изображения P, как правило, располагается вблизи главного фокуса объектива F 2 на расстоянии чуть меньше фокусного. Смещение плоскости P 2 в сторону объектива необходимо с целью улучшения резкости изображения на краях поля изображения, но за счет некоторого ухудшения его в центре. Величина этого смещения выражается долями миллиметра.
Плоскость P, в которой помещается светочувствительный материал (фотопленка или фотопластинка), называют плоскостью изображения. Расстояние от задней узловой точки объектива S 2 до плоскости изображения P называется фокусным расстоянием фотокамеры и обозначается буквой f.
 |
Плоскость изображения P называют плоскостью снимка, а само изображение – снимком. Центральные лучи AS 1 и BS 1 принято называть проектирующими лучами, так как они проектируют точки объекта на снимок. Поскольку расстояние между узловыми точками мало, можно считать, что они совпадают, и рассматривать одну точку S (рис. 2). Называют ее центром проекции. Таким образом, изображение на снимке строится проектирующими лучами, проходящими через общий центр проекции, поэтому можно считать, что изображение на снимке строится по законам центральной проекции (снимок – центральная проекция сфотографированного объекта).
Совокупность центральных проектирующих лучей точек фотографируемого объекта образует две связки: переднюю (входящие лучи) с вершиной в передней узловой точке объектива и заднюю (выходящие лучи) с вершиной в задней узловой точке объектива. Так как в идеальном случае каждый выходящий центральный луч параллелен соответствующему входящему лучу, то обе связки можно считать совершенно одинаковыми (конгруэнтными).
|
|
|
|
|
|
