 |
Вторичные дирекции: теория и расчеты
|
|
|
|
| Оглавление книги | |||

| |||
|
Изучение астрологии - это во многом изучение символики. Каждому фактору гороскопа придается особое значение. Каждая планета, знак и аспект, каждый дом и квадрант гороскопа имеют особый смысл и символизируют естественный принцип, действие которого можно проследить в разнообразных проявлениях повседневной жизни. К примеру, есть особый смысл в том, ч то в какой-то момент времени одна планета на небе находится выше всех остальных, или если одна планета расположена между двумя другими или является единственной обитательницей полушария гороскопа. Появления и поведение планет и их действительные астрономические перемещения также имеют особое значение для астролога. Например, Меркурий - это планета, расположенная к Солнцу ближе всех других известных планет, за год он обращается вокруг Солнца более четырех раз. Из-за своей близости к Солнцу и быстрого перемещения, по отношению к остальной части солнечной системы Меркурий играет роль небесного посланника, посредника, переводчика, изменяя и переводя лучи небесного Логоса. Следовательно, Меркурий символизирует энергию ума и способность к самовыражению, то есть те два фактора, которые помогают каждому человеку приспособиться к своему окружению.
|
|
|
Наша планетарная система состоит из одной большой звезды, расположенной в центре - Солнца - вокруг которой вращаются планеты по своим орбитам с различными скоростями. С точки зрения наблюдателя, стоящего на одной из этих планет, Солнце будет выглядеть движущимся телом, оно как бы совершает полный оборот в Зодиаке, в то время как в действительности это планета вращается вокруг Солнца. Такое (видимое) прохождение Солнца через двенадцать знаков Зодиака символизирует полный цикл жизненного опыта человека. Так как нас интересует исключительно влияние этих знаков на нашу планету, мы на Земле основываем нашу астрологию на видимом движении Солнца и действительном движении планет по отношению к нашей собственной планете. Земле требуется свыше 365 дней для того, чтобы совершить полный оборот вокруг Солнца. Следовательно, для нас на Земле это и есть тот символический период времени, который соответствует одному полному циклу жизненного опыта. Однако, есть и более быстрое движение Земли, которое также связано с кругом Зодиака.
Это движение - суточное вращение Земли вокруг своей оси. Из-за такого движения создается впечатление, что Солнце за сутки оборачивается вокруг Земли, происходит явление смены дня и ночи везде, за исключением полюсов. Если бы наблюдатель, стоящий на земном экваторе, целый день неотрывно смотрел бы на точку, расположенную прямо у него над головой, он бы увидел, как за двадцать четыре часа у него над головой прошел весь Зодиак. Таким образом, мы видим, что посредством вращения Земли вокруг собственной оси получается еще один полный кругооборот Зодиака. Хотя этот кругооборот и совершается за более короткий период времени, его также можно рассматривать как круг, символизирующий один завершенный цикл жизненного опыта.
|
|
|
То, что микрокосм отражает макрокосм - это закон природы. Этот закон нашел свое отражение в аксиоме - "Как вверху, так и внизу". Поэтому, если два цикла времени тесно связаны между «собой, мы можем считать, что меньший цикл содержит в себе потенциальные возможности большего. Вот почему мы вправе символически приравнять то время, которое требуется Земле для совершения одного оборота вокруг своей оси, то есть сутки, ко времени, которое требуется Земле для совершения одного полного оборота по своей орбите, то есть к году.
У тех изучающих астрологию студентов, которые не вполне сведущи в астрономии, могут возникнуть сомнения в том, что именно здесь имеется в виду под словом "день" или "сутки". Может возникнуть некоторая путаница относительно того, чем различаются "истинный солнечный день", "средний солнечный день" и "звездный день". Здесь уместно было бы дать некоторые пояснения этим трем различным способам измерения продолжительности суток.
Звездные сутки - это отрезок времени, за который Земля совершает один полный оборот вокруг своей оси относительно неподвижных звезд. Однако, в то время как земля вращается, она еще и движется по своей орбите вокруг Солнца. Для того, чтобы сделать один полный оборот относительно Солнца, Земле придется повернуться на своей оси несколько далее, для того, чтобы одна и та же точка на ее поверхности могла опять оказаться повернутой к Солнцу в конце каждых суток. Отрезок времени, необходимый Земле для совершения полного поворота вокруг своей оси относительно неподвижных звезд, составляет приблизительно 23 часа 56 минут. Это продолжительность звездных суток. Отрезок времени, необходимый Земле для совершения полного оборота вокруг своей оси относительно Солнца, бывает разным. Прежде всего, это происходит потому, что Земля вращается вокруг Солнца по эллиптической орбите, а это значит, что в какое-то время года Земля находится ближе к Солнцу, а в какое-то - дальше, а второе - из-за того, что эклиптика расположена под углом к экватору, а это значит, что квадранты эклиптики нельзя разделить на части так, чтобы это полностью соответствовало аналогичным частям квадрантов экватора. Для повседневной работы удобно пользоваться в качестве стандартной меры времени средней продолжительностью солнечного дня. Такой день, состоящий из 24 часов, известен как "средний солнечный день". "Истинный солнечный день" бывает длиннее или короче двадцати четырех часов, но не более, чем на 16 минут. Истинный солнечный день - это время, измеренное по солнечным часам. Разница между истинным солнечным днем и средним солнечным днем и является той причиной, почему Солнце редко оказывается прямо над головой в полдень по местному времени. Такое явление происходит лишь четырнадцать раз в году, когда продолжительность истинного солнечного дня точно совпадает с продолжительностью среднего солнечного дня. В Морском Сборнике публикуется набор таблиц для каждого дня в году, где приводится разница в минутах между продолжительностью среднего солнечного дня и истинного солнечного дня. Такой набор таблиц известен как "Уравнение времени".
|
|
|
Из вышеприведенных пояснений видно, что единственным "днем", который соответствует полному осевому обороту Земли относительно Солнца, является истинный солнечный день. Значит, по всем правилам следовало бы именно эту единицу времени приравнивать к более длинному циклическому периоду в один год. Однако, из практических соображений, достаточно производить вычисления, используя приблизительную единицу времени - средний солнечный день. Такая замена дает очень небольшую неточность, которой можно пренебречь, зато вычисления значительно упрощаются.
Система вторичных дирекций стала довольно популярной за счет сравнительной простоты связанных с ней вычислений. С другой стороны, расчет примарных дирекций требует применения тригонометрических формул. Необходимые построения, хотя и не сложные сами по себе, заставляют составителя проделывать кропотливую работу. Все, что требуется в системе вторичных дирекций - это отсчитать от даты рождения столько дней, сколько лет человеку, и затем свести в таблицу точные аспекты, образованные между планетарными позициями в карте рождения и планетарными позициями на полученный таким образом день. Это и будут те дирекции, которые будут действовать в течение этого года. Как уже говорилось в Главе I, отсчет дней от даты рождения следует производить как в прямом, так и в обратном порядке. Простота этого метода дает возможность получить представление о прямых и обратных вторичных дирекциях только на основании рассмотрения эфемерид.
|
|
|
Ненамного сложнее и расчет положения прогрессивного и обратного МС. МС радиксной карты продвигается вперед через Зодиак с той же скоростью, что и Солнце в дни после рождения, и движется через Зодиак в обратном направлении с той же скоростью, что и Солнце в дни, предшествующие рождению. Другими словами, МС всегда остается на том же зодиакальном расстоянии от Солнца, движется ли Солнце в Зодиаке вперед, как это имеет место в прямых вторичных дирекциях, или назад, как в случае обратных дирекций. Следовательно, для того, чтобы найти положение прогрессивного и обратного МС, необходимо лишь определить положение Солнца в Зодиаке в тот день, который соответствует нужному году. Если рассчитывать прямые дирекции, то нужно вычесть положение Солнца при рождении от его положения в день дирекции и полученную таким образом величину дуги прибавить к радиксному МС. Если рассчитываются обратные дирекции, то положение Солнца в день дирекции нужно вычесть из его положения при рождении и эту величину дуги вычесть из радиксного МС.
Здесь нужно сделать два замечания. Поскольку изменения в скорости перемещения Солнца в течение какого-то отдельного дня бесконечно малы, то вполне достаточно производить расчеты на основании разности между положением Солнца в полдень дня рождения и в полдень дня дирекции. Мы видим, что это эквивалентно измерению в средних солнечных днях, а не в истинных солнечных днях, хотя теоретически, как мы уже говорили, именно истинный солнечный день символизирует отрезок времени в один год. Однако с практической точки зрения вполне достаточно использовать в вычислениях средний солнечный день. Максимально возможные колебания в продолжительности истинных солнечных дней в интервале времени в сто дней, которого вполне достаточно для рассмотрения жизненного периода большинства людей, составляет тридцать одну минуту. За тридцать одну минуту Солнце проходит дугу величиной около одной угловой минуты и шестнадцати секунд. Это и есть максимальная ошибка, возможная при таком допущении. Поскольку обычно нет никакой необходимости рассчитывать прогрессивное положение МС с точностью большей, чем четверть градуса, то мы видим, что можно вполне пренебречь этой максимальной разницей в угловую минуту с небольшим, которая может получиться из-за использования в вычислениях среднего солнечного дня.
|
|
|
Как только мы рассчитали прогрессивный МС, нам осталось найти по соответствующим таблицам домов асцендент для данной широты места рождения.
В качестве иллюстрации возьмем следующий пример расчета вторичных дирекций {см. рис. 1).
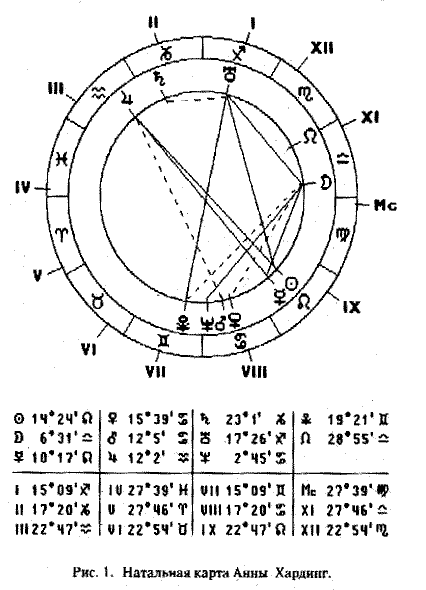
Анна Хардинг, популярная киноактриса прошлых лет, родилась 7 августа 1902 года в Хьюстоне, Техас (29°47' с.ш., 95°20' з.д.) в 9 часов 12 минут пополудня по Гринвичу. Радиксный МС был 27°39' Девы. Требуется рассчитать дирекции на двадцать четвертый день рождения. Прежде всего нужно рассчитать положение прогрессивного МС следующим образом:
| Дата рождения | 7 августа 1902 |
| 24 дня после рождения приходится на | 31 августа 1902 |
| Положение Солнца в полдень 31 августа 1902 | 7°  08' 08'
|
| Положение Солнца в полдень рождения | 14°  02' 02'
|
| Разность | 23° 06' |
| Положение радиксного МС | 27°  39' 39'
|
| Прибавляем разность между положениями Солнца | 23° 06' |
| Положение прогрессивного МС | 20°  45' 45'
|
| По таблицам домов для 29°47' с.ш. находим, что асцендент, соответствующий этому значению МС | 4°  26' 26'
|
| Теперь рассчитываем обратный МС: | |
| 24 дня до рождения выпадает на | 14 июля 1902 |
| Положение Солнца в полдень на дату рождения | 14°  02' 02'
|
| Положение Солнца на 14 июля 1902 года | 21°  05' 05'
|
| Разность | 22° 57' |
| Положение радиксного МС | 27°  39' 39'
|
| Вычитаем разность между положениями Солнца | 22° 57' |
| Положение обратного МС | 4°  42' 42'
|
| По таблицам домов для 29°47' с.ш., находим, что асцендент, соответствующий этому значению МС | 27°  07' 07'
|
Следующий шаг - пронаблюдать, находятся ли прогрессивные прямой и обратный МС и асцендент в градусе точного аспекта с какой-нибудь планетой. В этом отношении одинаково необходимо учитывать аспекты полусекстиля, полуквадрата, полутораквадра-та и квинтиля, а также соединение, секстиль, квадратуру, трин и оппозицию. Мы увидим, что следующий аспект является единственным, который образовался между этими двумя наборами позиций:
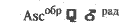
Теперь нужно свести в таблицу все аспекты, образованные между планетами на 31 августа 1902 года и 14 июля 1902 года и МС и асцендентом катального рисунка, восходящий градус которого составляет 15°09' Стрельца.
Прогрессивные планетарные позиции можно либо рассчитать на то же время дня, в которое родился данный человек, или использовать положение планет в полдень. В первом случае планетарные позиции будут относиться к дню рождения, во втором (Метод Полуденной Даты) - к иному дню, если только человек не родился в полдень. Подробнее Метод Полуденной Даты освещен на следующих страницах. Величину суточного перемещения каждой планеты, соответствующего какой-то части года, можно легко вычислить через соотношение двухчасового перемещения, что соответствует месяцу (см. таблицу лунных прогрессий на последующих страницах). Для планетарных прогрессий составлять такую таблицу нет необходимости, поскольку суточное перемещение планет значительно меньше, чем перемещение Луны. Поэтому почти всегда мы можем оценить визуально положение планет, рассмотрев их полуденные положения.
Прогрессивные аспекты будут такими:

Следующее действие - выписать все аспекты между прогрессивными МС и асцендентом и планетами на 31 августа и 14 июля 1902 года. Образовался только один аспект:
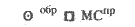
Последняя серия угловых дирекций включает в себя все аспекты, образованные между обратными МС и асцендентом и планетами на 31 августа и 14 июля 1902 г. Образовался только один аспект:

Теперь нужно рассчитать и свести в таблицу солнечные дирекции в той же последовательности, что и дирекции к углам. Прежде всего нужно выписать все аспекты между прогрессивным Солнцем и планетами на радиксной карте, а затем все аспекты, образованные радиксным Солнцем и прогрессивными и обратными планетами. В заключении нужно свести в таблицу аспекты, образованные между прогрессивным Солнцем и прогрессивными и обратными планетами и между обратным Солнцем и теми же планетами. Следующие солнечные дирекции соответствуют двадцать четвертому дню рождения: -

Теперь следует свести в таблицу межпланетарные дирекции, в той же последовательности, что и солнечные дирекции, причем каждый раз берется по одной планете и выписываются прежде всего все аспекты, образованные между прогрессивной планетой и планетами в радиксном гороскопе. Затем следует отметить аспекты между той же планетой в радиксной карте и прогрессивными и обратными планетами, и наконец аспекты, образованные между прогрессивной и обратной планетой и другими прогрессивными и обратными планетами. Ниже приводятся межпланетарные дирекции, соответствующие двадцать четвертому дню рождения:
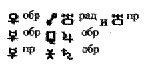
Мы уже имели дело со всеми видами прогрессивных аспектов кроме тех, что образованы прогрессивной Луной. Среднесуточное перемещение Луны составляет около двенадцати градусов, или один градус за каждые два часа. При соотнесении "день за год" два часа соответствуют одному месяцу. Отсюда мы видим, что аспекты, составленные прогрессивной Луной, образуются и распадаются довольно быстро, и поэтому их воздействие едва ли продолжается долее двух месяцев. Поскольку расчет прогрессивных аспектов Луны гораздо сложнее, чем расчет месячных, недельных и суточных серий вторичных прогрессий, то на практике можно с большей легкостью получить уточнение сроков годовых вторичных дирекций, использую эти три серии. Тем не менее, для завершенности изложения и для блага тех, кто, возможно, не захочет отказаться от метода прогнозирования, пользовавшегося в прошлом довольно; широкой популярностью, мы посвятим один-два абзаца рассмотрению лунных вторичных дирекций.
Для упрощения расчета лунных вторичных дирекций удобно применять метод, известный как "полуденная дата". "Полуденная дата" соответствует тому отрезку года, который представлен разностью во времени между полуднем (по Гринвичу) дня рождения и истинным временем рождения в расчете "день за год". Следовательно, два часа соответствуют одному месяцу, а четыре минуты - одному дню. Если рождение имело место до полудня, количество часов и минут, прошедших от момента рождения до полудня, переводится в месяцы и дни согласно вышеупомянутому соотношению, а получившееся в результате количество месяцев и дней отсчитывается по календарю от дня рождения и получается Полуденная Дата. Если рождение произошло после полудня, количество часов и минут от полудня до момента рождения аналогичным образом переводится в обратном направлении от дня рождения и получается Полуденная Дата. Эта дата действенна в отношении прямых дирекций. Чтобы рассчитать Полуденную Дату относительно обратных дирекций, весь процесс как-бы переворачивается, т.е. если рождение имело место до полудня, то количество дней отсчитывается по календарю в обратную сторону, а если после полудня - то в прямом направлении. Теперь эти новые даты можно использовать как базу для всех последующих вычислений, основанных на полуденных • позициях планет.
Теперь мы рассчитаем полуденные даты для гороскопа Анны Хардинг. Поскольку она родилась в 9 часов 12 минут пополудни по Гринвичу, полуденная дата для прямых дирекций выпадет на день года, предшествующий дате рождения, в то время, как Полуденная Дата для обратных дирекций - на день года после дня рождения. Для того, чтобы определить, сколько именно дней нужно отсчитать от дня рождения в обратном направлении, необходимо вычислить, какая часть года соответствует девяти часам двенадцати минутам при соотношении "два часа за месяц" и "четыре минуты за день". Отсюда мы получаем, что девять часов двенадцать минут соответствуют 138 дням. Если от 7 августа 1902 года отсчитать в обратную сторону сто тридцать восемь дней, то в качестве полуденной даты для прямых дирекций мы получаем 22 марта. Если тот же период отсчитать от 7 августа в прямом направлении, то в качестве обратной полуденной даты мы получаем 23 декабря.
Теперь нужно рассчитать лунные дирекции, соответствующие двадцать четвертому дню рождения. Получив полуденную дату, следующим действием мы определяем истинное суточное перемещение Луны на день дирекции, соответствующий нужному нам году. Затем это суточное перемещение делится на двенадцать, для того, чтобы получить величину дуги, которую Луна проходит за два часа, что соответствует одному месяцу жизни. 31 августа 1902 года, т.е. в день прогрессивных дирекций, который соответствует двадцать пятому году жизни Анны Хардинг, в полдень Луна занимала положение 14°ЗГ02" Льва. В полдень следующего дня положение Луны было 28°42'48" Льва. Следовательно, суточное перемещение составило 14°12'. (Для практических целей достаточно рассчитать суточное перемещение Луны с точностью до одной минуты дуги.) Поделив 14°12' на двенадцать, мы можем получить величину перемещения Луны за два часа, что соответствует периоду в один месяц. За каждые два часа Луна в среднем проходит 1°11'. Последовательно прибавляя приращение в 1°11' к положению Луны на полдень 31 августа, можно составить следующую таблицу, показывающую положение прогрессивной Луны и тех аспектов, которые она образует для каждого месяца года:
Полуденная дата = 22 марта

Теперь следует подготовить аналогичную таблицу, чтобы показать обратные лунные дирекции. В этом случае необходимо вычитать месячное приращение из полуденного положения Луны на день обратной дирекции. Расчеты выглядят следующим образом:
| Положение Луны в полдень 14 июля 1902 | 13°  03'52" 03'52"
|
| Положение Луны в полдень 13 июля 1902 | 1°  03'11" 03'11"
|
| Суточное перемещение Луны | 12°01' |
| Месячное приращение -1/12 суточного перемещения Луны | 1°00' |

Чтобы восстановить ту минуту, которую мы потеряли, округляя одну двенадцатую суточного перемещения Луны, приращение седьмого месяца было взято в 1°01'.
В следующей главе, где будет идти речь об интерпретации дирекций, мы будем ссылаться на дирекции, основанные на карте Анны Хардинг.
|
|
|



 Глава I. Четыре основных принципа в методе вторичных дирекций
Глава I. Четыре основных принципа в методе вторичных дирекций