Повторение испытании. Формула Бернулли. Формула Пуассона. Локальная и интегральная теоремы Муавра и Лапласа.

Классическое определение вероятности Колмагорова

Предположим, что мы имеем дело с пространством элементарных исходов, состоящим из конечного числа n элементов: Более того, предположим, что из каких- либо соображений мы можем считать элементарные исходы равновозможными. Тогда вероятность любого из них принимается равной 1/ n.

Эти соображения чаще всего не имеют отношения к математической модели и основаны на какой-либо симметрии в эксперименте (симметричная монета, правильная кость). Либо мы можем заранее считать исходы экс-та равновозможными, но тогда рано или поздно возникнет вопрос о соответствии такой мат. модели реальному эксперименту.

Если событие состоит из m элементарных исходов, то вероятность этого события равняется

Определение. Говорят, что эксперимент удовлетворяет классическому определению вероятности (или классической вероятностной схеме), если пространство элементарных исходов состоит из конечного числа равновозможных исходов.

В этом случае вероятность любого события А равна отношению числа исходов, благоприятствующих событию А, к общему числу исходов.

Геометрическая вероятность

Классическое определение вероятности пригодно только для экспериментов с ограниченным числом равномерных элементарных событий.

 

Рассмотрим какую-нибудь непрерывную квадрируемую область в , (на прямой, на плоскости, в пространстве). Предположим, что «мера» (длина, площадь, объём, соответственно) конечна. Пусть случайный эксперимент состоит в том, что мы наудачу бросаем в эту область точку . Термин «наудачу» здесь означает, что вероятность попадания в любую часть не зависит от формы или расположения A внутри , а зависит лишь от «меры» области.

Определение. Эксперимент удовлетворяет условиям «геометрического определения вероятности», если его исходы можно изобразить точками некоторой области в так, что вероятность попадания точки в не зависит от формы или расположения A внутри , а зависит лишь от «меры» области A (и следовательно, пропорциональна этой мере):

, где обозначает меру обл. A.

«Мерой» мы пока будем называть длину, площадь, объём.

Если для точки, брошенной в область , выполнены условия геометрического определения вероятности, то говорят, что точка равномерно распределена в области .

Замечание. Если даже эксперимент удовлетворяет геометрическому определению вероятности, далеко не для всех множеств вероятность может быть вычислена как отношение меры А к мере . Причиной этого является существование так называемых «неизмеримых» множеств, то есть множеств, мера которых не существует. А если для всех подмножеств мы можем определить их вероятности, следует сузить класс множеств, называемых «событиями», оставив в этом классе только те множества, для которых мы можем определить вероятность.

Формула полной вероятности.

Пусть событие А может наступить только при условии появления одного из несовместных событий H_i (гипотез), которые образуют полную группу. Тогда вероятность любого события А может быть вычислена по формуле:

.

События H₁, H₂,…, образующие полную группу событий, часто наз. гипотезами. При подходящем выборе гипотез для произвольного события А могут быть сравнительно просто вычислены P(A\H_i) (вероятность событию А произойти при выполнении H_i).

Формула Байеса.

Пусть H₁, H₂,…- полная группа событий и А- некоторое событие положительной вероятности. Тогда условная вероятность того, что имело место событие H_k, если в результате эксперимента наблюдалось событие А, может быть вычислена по формуле:

.

Формулы Байеса позволяют переоценивать вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.

Повторение испытании. Формула Бернулли. Формула Пуассона. Локальная и интегральная теоремы Муавра и Лапласа.

Пусть проводится n испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания наз. независимыми относительно соб. А.

Повторные независимые испытания наз. испытаниями Бернулли, если при каждом испытании имеются только два возможных исходов и вероятности этих исходов остаются неизменными для всех испытаний. Одному испытанию Бернулли соответствует множество элементарных исходов состоящее из 2-х элемен. событий.

- неудача (0), - успех (1)

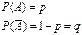
множество элементарных исходов для n испытаний состоит из 2ⁿ элемент. исходов , которые представляют собой последовательности состоящие из 0 и 1, соответствующие результату испытаний на каждом этапе

Формула Бернулли. Вероятность того, что при n испытаниях событие А произойдет ровно m раз. И Þ не произойдет n-m раз выражает формула Бернулли.

Если число испытаний велико, а вероятность успеха мала, то вероятность m успехов в n испытаниях рассчитывается по формуле Пуассона.

Th. Пуассона. Если при и 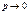, так что , то вероятность m успехов в n испытаниях Бернулли вычисляется по формуле Пуассона:

.

Условие применения формулы Пуассона:

При больших n пользуются локальной теоремой Муавра- Лапласа, которая дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления события m раз из n испытаний, если число испытаний достаточно велико.

Th. Если вероятность Р появления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность P_n(m) того, что событие А появится в n испытаниях ровно m раз, приближенно равна (тем точнее, чем больше n) значению функции:

при

Для вычисления функции имеются таблицы.

Пусть проводится n испытании, в каждом из которых вероятность события А появиться в n испытаниях не менее m₁ и не более m₂ раз, существует интегральная теорема Муавра- Лапласа: если вероятность Р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие А появится в n испытаниях от m₁ до m₂ раз, приближенно равна определенному интегралу:

,где ,

если npq<20, то

Поделиться:

Воспользуйтесь поиском по сайту: