 |
Алгоритм Дейкстры решения задачи о кратчайшем пути.
|
|
|
|
Задача о кратчайшем пути и алгоритм Дейкстры ее решения
Пусть задан орграф G(V, E), каждой дуге 
которого поставлено в соответствие число 
, называемое длиной дуги.
Определение. Длиной пути называется сумма длин дуг, составляющих этот путь. Задача о кратчайшем пути ставится так.
Вариант 1. Найти длины кратчайших путей (путей минимальной длины) и сами пути от фиксированной вершины s до всех остальных вершин графа.
Вариант 2. Найти длины кратчайших путей и сами пути между всеми парами вершин данного графа.
Если в графе имеются дуги отрицательной длины, задача может не иметь решений (потеряет смысл). Это происходит из-за того, что в графе может присутствовать контур отрицательной длины. Наличие контуров отрицательной длины означает, что длину пути можно сделать равной 
. А если контуров отрицательной длины нет, то кратчайшие пути существуют и любой кратчайший путь – это простая цепь.
Заметим, что если кратчайший путь существует, то любой его подпуть – это тоже кратчайший путь между соответствующими вершинами.
Алгоритм Дейкстры решения задачи о кратчайшем пути.
Алгоритм работает с дугами положительной длины и определяет кратчайшие пути от фиксированной вершины s до всех остальных вершин графа. Обозначим эти вершины v 1 ,v 2 ,…,vn.
Определение. Назовем вершину u лежащей ближе к вершине s, чем вершина v, если длина кратчайшего пути от s до u меньше длины кратчайшего пути от s до v. Будем говорить, что вершины u и v равноудалены от вершины s, если длины кратчайших путей от s до u и от s до v совпадают.
Алгоритм Дейкстры последовательно упорядочивает вершины графа в смысле близости к вершине s и основан на следующих базовых принципах.
|
|
|
Если длины дуг – положительные числа, то
ü ближайшая к s вершина – она сама. Длина кратчайшего пути от s до s равна 0;
ü ближайшая к s вершина, отличная от s, лежит от s на расстоянии одной дуги - самой короткой из всех дуг, выходящих из вершины s;
ü любая промежуточная вершина кратчайшего пути от s до некоторой вершины v лежит ближе к s, чем конечная вершина v;
ü кратчайший путь до очередной упорядоченной вершины может проходить только через уже упорядоченные вершины.
Пусть алгоритм уже упорядочил вершины v 1 ,v 2 … vk. Обозначим через 
, 
длину кратчайшего пути до вершины vi.
Рассмотрим все дуги исходного графа, которые начинаются в одной из вершин множества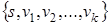 
и оканчиваются в еще неупорядоченных вершинах. Для каждой такой дуги, например 
, вычислим сумму 
. Эта сумма равна длине пути из s в y, в котором вершина vi есть предпоследняя вершина, а путь из s в vi – кратчайший из всех путей, соединяющих s и vi.
Этим самым определены длины всех путей из s в еще не упорядоченные вершины, в которых промежуточными вершинами являются только вершины из числа k ближайших к s. Пусть кратчайший из этих путей оканчивается на вершине w. Тогда w и есть 
по близости к s вершина.
Технически действия по алгоритму Дейкстры осуществляются при помощи аппарата меток вершин. Метка вершины v обозначается как 
. Всякая метка – это число, равное длине некоторого пути от s до v. Метки делятся на временные и постоянные. На каждом шаге только одна метка становиться постоянной. Это означает, что ее значение равно длине кратчайшего пути до соответствующей вершины, а сама эта вершина упорядочивается. Номер очередной упорядоченной вершины обозначим буквой р.
Описание алгоритма.
Шаг 1. (Начальная установка). Положить 
и считать эту метку постоянной. Положить 
, 
и считать эти метки временными. Положить 
.
Шаг 2. (Общий шаг). Он повторяется n раз, пока не будут упорядочены все вершины графа.
|
|
|
Пересчитать временную метку всякой неупорядоченной вершины vi, в которую входит дуга, выходящая из вершины р, по правилу 
Выбрать вершину с минимальной временной меткой. Если таких вершин несколько, выбрать любую.
Пусть w- вершина с минимальной временной меткой. Считать метку 
постоянной и положить 
.
Шаги алгоритма Дейкстры удобно оформлять в таблице, каждый столбец которой соответствует вершине графа. Строки таблицы соответствуют повторению общего шага.
Пример. Для графа на рис. 4. найти кратчайшие пути от вершин 
до всех остальных вершин графа. Ребра означают две разнонаправленные дуги одинаковой длины.
Решение. В табл. 1 записаны метки вершин на каждом шаге. Постоянные метки помечены знаком «+». Подробно опишем, как вычисляются метки вершин.
1. Из вершины 1 выходят дуги в вершины 2, 5, 6. Пересчитываем метки этих вершин и заполним вторую строку таблицы.
; 
; 
.
Метка вершины 6 становиться постоянной, 
.
2. Из вершины 6 выходят дуги в еще неупорядоченные вершины 2, 5, 8, 9. Пересчитываем их временные метки
; 
;
; 
.
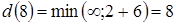Заполняем 3 строку таблицы. Минимальная из временных меток равна 3 (метка вершины 9),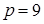 
.
3. Из вершины 9 выходят дуги в еще неупорядоченные вершины 5, 8, 11, 12. Тогда
; 
;
; 
.
Заполняем четвертую строку таблицы. В этой строке две вершины - 2 и 12 имеют минимальные временные метки, равные 4. Сначала упорядочим, например, вершину 2. Тогда на следующем шаге будет упорядочена вершина 12.
Таблица 1
| 
|
|
|
|
|
|
|
|
|
|
| p =1 | |
|
|
|
| 
|
|
|
|
|
|
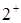
| p =6 | |||
|
|
|
|
|
| 
|
|
|
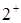
| p =9 | ||||
|
| 
|
|
|
|
|
|
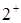
| p =2 | |||||
|
|
|
|
|
|
|
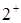
| p =12 | ||||||
|
|
| 
|
|
|
|
|
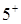
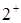
| p =5 | |||||
|
|
|
|
|
|
|
|
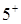
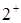
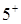
| p =8 | |||||
|
|
|
|
|
|
| 
|
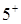
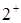
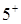
| p =11 | |||||
|
|
| 
|
|
|
|
|
|
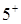
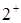
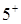
| p =4 | ||||
|
|
| 
|
|
|
|
|
|
|
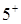
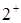
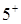
| p =3 | |||
|
|
|
|
|
|
| 
|
|
|
|
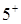
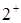
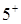
| p =7 | ||
| 0+ |
|
|
|
|
|
|
|
| 
|
|
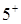
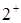
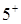
| p =10 |
Итак, 
.
4. Из вершины 2 выходят дуги в еще неупорядоченные вершины 3, 4, 5. Пересчитываем временные метки этих вершин
; 
; 
.
Заполняем 5 строку таблицы. Минимальная из временных меток равна 4 (метка вершины 12), 
.
5. Из вершины 12 выходят дуги в еще неупорядоченные вершины 8, 11,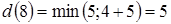 
; 
.
|
|
|
Заполняем 6 строку таблицы. Минимальная из временных меток равна 5 (метка вершины 5), 
.
6. Из вершины 5 выходят дуги в еще неупорядоченные вершины 3, 4, 7, 8, 
; 
; 
;
.
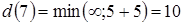Заполняем 7 строку таблицы. Становиться постоянной метка вершины 8 (она равна 5), 
.
7. Из вершины 8 выходят дуги в неупорядоченные вершины 4, 7, 10, 11. Следовательно, ; 
; 
; 
.
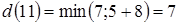Вершина 11 упорядочивается.
8. Из вершины 11 выходят дуги в неупорядоченные вершины 7, 10. Пересчитываем временные метки этих вершин
; 
.
Вершина 4 получает постоянную метку.
9. Из вершины 4 выходят дуги в неупорядоченные вершины 3, 7. Пересчитываем временные метки
; 
.
Упорядочиваем вершину 3.
10. Из вершины 3 выходят дуги, входящие в уже упорядоченные вершины. Ни одну метку изменить нельзя. Одиннадцатая строка таблицы повторяет десятую. А минимальная из временных меток - это метка вершины 7, поэтому 
.
11. Из вершины 7 выходит дуга в неупорядоченную вершину 10,
.
Заполняем 12 строку таблицы. На этом шаге упорядочиваем последнюю неупорядоченную вершину 10.
|
|
|
