 |
Контрольные карты. Контроль по количественному признаку
|
|
|
|
Среднее значение и размах
Одним из способов достижения удовлетворительного качества и поддержания его на этом уровне является применение контрольных карт.
Наибольшее распространение получили контрольные карты среднего значения 
и контрольные карты размаха R, которые используются совместно или раздельно.
Приведем пример. В сосудах 1,2,3,… находятся деревянные палочки, на которых нанесены числа –10,-9,…,-2,-1,0,1,2,…,9,10. Палочки имитируют изделия, а нанесенные на них числа означают отклонения контролируемого размера от номинального в сотых долях процента. В каждом сосуде находится N палочек, которые можно рассматривать как изделия, изготовленные за заданный интервал времени, называемый периодом отбора выборок или проб. Значения N предполагается большим, так что на нескольких палочках может быть нанесено одно и тоже число, некоторые палочки могут быть единственными носителями определенных чисел, более того, возможно, что в каком-нибудь сосуде не окажется вообще палочки с определенным числом. После тщательного перемешивания палочек в сосудах извлекается из каждого сосуда выборка объемом n палочек, например n=5. При этом тщательное перемешивание обеспечивает случайность выбора палочек. Записав числа, нанесенные на оказавшихся в очередных выборках палочках, подсчитывают их средние арифметические значения и наносят как ординату точки с абсциссой, соответствующей номеру сосуда. Если точка окажется внутри начерченных на контрольной карте границ, то имитируемый описанной моделью процесс считается налаженным, в противном случае – требующим корректировки.
Статистикой принято называть функцию случайных величин, полученных из одной совокупности, которая используется для оценки определенного параметра этой совокупности.
|
|
|
Пусть 
- результаты наблюдений, образующие одну выборку объемом n. Выборочное среднее арифметическое значение определяется как 
(i=1,2,…,n)
Размах этой выборки 
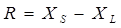, где
- максимальный результат наблюдений в выборке,
- минимальный результат наблюдений в выборке.
Пусть взято двадцать пять выборок, состоящих из пяти образцов каждая. Среднее арифметическое значение и размах определяются для каждой выборки отдельно. Они наносятся на контрольные карты средних арифметических значений и размахов.
Таблица 2‑1. Учет результатов наблюдений
Далее находим среднее значение всех измерений, или общее среднее. Это можно выполнить при помощи сложения суммарной колонки и деления суммы на количество выборок (следует учесть, что некоторые из этих величин – отрицательные). Если обозначим количество выборок через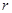 
(в данном случае равное 25), то общее среднее 
можно определить по следующей формуле 
.
Затем определяем средний размах, разделив сумму разных значений размаха на количество выборок: 
. После этого значения и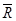 
наносятся на контрольные карты в качестве контрольных линий.
Далее для контрольных карт определяются следующие границы регулирования:
· верхняя граница регулирования для контрольной карты средних арифметических значений 
;
· нижняя граница регулирования контрольной карты средних арифметических значений 
;
· верхняя граница регулирования контрольной карты размаха 
;
· нижняя граница регулирования контрольной карты размаха 
, где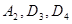 
– коэффициенты, зависящие от объема выборки. Если выборка содержит 5 образцов (n =5), то 
Рис. 2‑1. Контрольная карта, для данных, приведенных в таблице 2-1. Среднее значение
Рис. 2‑2. Контрольная карта, для данных, приведенных в таблице 2-1. Размах
|
|
|
|
|
|
