Расчеты электрических цепей с помощью законов Кирхгофа.

Теперь давайте рассмотрим вариант сложной цепи, и я вам расскажу, как на практике применять законы Кирхгофа.

Итак, на рисунке 4 имеется сложная цепь с двумя источниками ЭДС величиной E₁=12 в и E₂=5 в, с внутренним сопротивлением источников r₁=r₂=0,1 Ом, работающих на общую нагрузку R = 2 Ома. Как же будут распределены токи в этой цепи, и какие они имеют значения, нам предстоит выяснить.

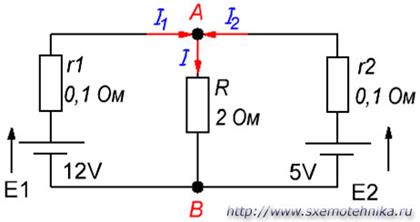
Рисунок 4. Пример расчета сложной электрической цепи.

Теперь согласно первому закону Кирхгофа для узла А составляем такое выражение:

I = I₁ + I₂,

так как I₁ и I ₂ втекают в узел А, а ток I вытекает из него.

Используя второй закон Кирхгофа, запишем еще два выражения для внешнего контура и внутреннего левого контура, выбрав направление обхода по часовой стрелке.

Для внешнего контура:

E₁-E₂ = Ur₁ – Ur₂ или E₁-E₂ = I₁*r₁ – I₂*r₂

Для внутреннего левого контура:

E₁ = Ur₁ + UR или E₁ = I₁*r₁ + I*R

Итак, у нас получилась система их трех уравнений с тремя неизвестными:

I = I₁ + I₂;

E₁-E₂ = I₁*r₁ – I₂*r₂;

E₁ = I₁*r₁ + I*R.

Теперь подставим в эту систему известные нам величины напряжений и сопротивлений:

I = I₁ + I₂;

7 = 0,1I₁ – 0,1I₂;

12 = 0,1I₁ +2I.

Далее из первого и второго уравнения выразим ток I₂

I₂=I - I₁;

I₂ = I₁ – 70;

1₂ = 0,1I₁ + 2I.

Следующим шагом приравняем первое и второе уравнение и получим систему из двух уравнений:

I - I₁= I₁ – 70;

1₂ = 0,1I₁ + 2I.

Выражаем из первого уравнения значение I

I = 2I₁– 70;

И подставляем его значение во второе уравнение

12 = 0,1I₁ + 2(2I₁ – 70).

Решаем полученное уравнение

12 = 0,1I₁ + 4I₁ – 140.

12 + 140= 4,1I₁

I₁=152/4,1

I₁=37,073 (А)

Теперь в выражение I = 2I₁– 70 подставим значение

I₁=37,073 (А) и получим:

I = 2*37,073 – 70 = 4,146 А

Ну, а согласно первому закона Кирхгофа ток I₂=I - I₁

I₂=4,146 - 37,073 = -32,927

Знак «минус» для тока I₂ означает, то что мы не правильно выбрали направление тока, то есть в нашем случае ток I ₂ вытекает из узла А.

 

15 Магнитное поле электрического тока, его графическое изображение. Характеристики магнитного поля: магнитодвижущая сила, напряженность, магнитная индукция, магнитный поток, магнитная проницаемость.

Магнитное поле и его характеристики. При прохождении электрического тока по проводнику вокруг него образуется магнитное поле. Магнитное поле представляет собой один из видов материи. Оно обладает энергией, которая проявляет себя в виде электромагнитных сил, действующих на отдельные движущиеся электрические заряды (электроны и ионы) и на их потоки, т. е. электрический ток. Под влиянием электромагнитных сил движущиеся заряженные частицы отклоняются от своего первоначального пути в направлении, перпендикулярном полю (рис. 34). Магнитное поле образуется только вокруг движущихся электрических зарядов, и его действие распространяется тоже лишь на движущиеся заряды. Магнитное и электрические поля неразрывны и образуют совместно единое электромагнитное поле. Всякое изменение электрического поля приводит к появлению магнитного поля и, наоборот, всякое изменение магнитного поля сопровождается возникновением электрического поля. Электромагнитное поле распространяется со скоростью света, т. е. 300 000 км/с.

Графическое изображение магнитного поля. Графически магнитное поле изображают магнитными силовыми линиями, которые проводят так, чтобы направление силовой линии в каждой точке поля совпадало с направлением сил поля; магнитные силовые линии всегда являются непрерывными и замкнутыми. Направление магнитного поля в каждой точке может быть определено при помощи магнитной стрелки. Северный полюс стрелки всегда устанавливается в направлении действия сил поля.

Напряженность магнитного поля, то есть силу магнитного поля оценивают по густоте магнитных силовых линий в данной точке поля. Напряженность магнитного поля обоз­начают в формулах буквой Н. Напряженность магнитного поля показывает число силовых линий магнитного поля, проходящих через 1 см² поперечного сечения поля.

Магнитная индукция это способность влиять магнитным полем на объект.

При помещении в катушку железного стержня (сердеч­ника) ее магнитный поток увеличивается во много раз. Объ­ясняется это следующим. Железо имеет кристаллическое строе­ние. Отдельные кристаллы железа, вследствие того, что внутри их происходит круговое движение электронов, т. е. существуют электрические токи, обладают свойствами маленьких магни­тиков. В обычном состоянии эти молекулярные магнитики рас­положены в беспорядке. Магнитные поля их взаимно нейтра­лизуются, и поэтому кусок железа в целом не проявляет маг­нитных свойств.

При помещении железа в магнитное поле молекулярные магнитики подобно магнитной стрелке компаса поворачиваются на некоторый угол и устанавливаются вдоль силовых линий магнитного поля. Чем сильное магнитное поле, тем большее число молекулярных магнитиков поворачивается и тем одно­роднее становится их расположение. Поля одинаково ориен­тированных магнитов не нейтрализуют уже друг друга, а на­оборот, складываются, создавая дополнительные силовые линии.

Магнитный поток, создаваемый элементарными магнити­ками железа, во много раз больше основного магнитного по­тока, создаваемого катушкой; именно поэтому магнитный поток катушки при помещении в нее железного сердечника увеличивается во много раз.

Магнитный поток Ф, проходящий через какую-либо поверхность, определяется общим числом магнитных силовых линий, пронизывающих эту поверхность, например катушку 1 (рис. 37, а), следовательно, в однородном магнитном поле

Ф = BS (40)

где S — площадь поперечного сечения поверхности, через которую проходят магнитные силовые линии.

Если постепенно увеличивать ток, протекающий по виткам катушки, то магнитный поток в железном сердечнике будет увеличиваться до тех пор, пока все молекулярные магнитики не повернутся точно по направлению силовых линий магнит­ного поля (рисунок 2). После этого возрастание магнитного по­тока за счет железа прекратится. Это состояние железного сердечника называется магнитным насыщением.

Число, показывающее, во сколько раз увеличивается маг­нитный поток соленоида при введении в него сердечника из какого-нибудь материала, называется магнитной проницае­мостью данного материала и обозначается буквой µ

Магнитная проницаемость некоторых сортов железа и спе­циальных сплавов достигает нескольких сотен тысяч. Для боль­шинства же материалов она близка к единице.

Произведение из напряженности магнитного поля Н на проницаемость материала µ называется магнитной индук­цией В.

Таким образом

B = µ *H.

Магнитная индукция определяет количество силовых линий в данном материале, проходящих через 1 см² поперечного се­чения материала.

После прекращения тока в катушке сердечник, если он сделан из мягкого железа, теряет свои магнитные свойства, потому что молекулярные магнитики снова располагаются бес­порядочно. Если же сердечник стальной, то он сохраняет при­обретенные магнитные свойства и после прекращения действия на него магнитного поля катушки. Объясняется это тем, что в стали молекулярные магнитики сохраняют свое упорядочен­ное расположение и после прекращения тока в катушке.

 

16 Проводник с током в магнитном поле. Электромагнитная сила. Правило левой руки.

Электромагнитная сила определяется законом Ампера. Он формулируется следующим образом. Электромагнитная сила, действующая на проводник с током, находящийся в магнитном поле и расположенный перпендикулярно направлению поля, равна произведению силы тока I, индукции магнитного поля В и длины проводника l:

F = IBl (48)

Если угол α между направлением тока и направлением линий магнитного поля не равен 90˚, то сила F пропорциональна sinα, т.е. в этом случае:

F = B·I·l·sinα,

а её направление следует по - прежнему определять по правилу левой руки. Отсюда видно, если провод расположен параллельно магнитным линиям, то sinα = 0 и F также равна нулю.

 

Правило левой руки

Для быстрого определения направления движения проводника с током помещенного в, постоянное магнитном поле существует так называемое правило левой руки.

Правило левой руки звучит так: если поместить левую руку между полюсами магнита так, чтобы магнитные силовые линии входили в ладонь, а четыре пальца руки совпадали с направлением движения тока в проводнике, то большой отогнутый палец укажет на направление движения проводника.

Другими словами попроще, можно сказать, что на проводник с током, действует некоторая сила, стремящаяся вытолкнуть его перпендикулярно магнитным силовым линиям. Опытным путем можно узнать и ее величину. Оказывается, что сила, с которой магнитное поле воздействует на проводник с током, прямо пропорциональна силе тока и длине той части проводника, которая помешена в магнитном поле.

Это правило подходит для частного случая, если проводник находится под прямым углом к магнитным силовым линиям. Если же проводник с током расположен не под прямым углом к магнитным силовым линиям, то сила, действующая на него, будет пропорциональна силе тока в проводнике и длине проекции части проводника, находящейся в магнитном поле, на плоскость, перпендикулярную магнитным силовым линиям. Отсюда сразу напрашивается вывод: если проводник параллелен магнитным силовым линиям, то сила, действующая на него, равна нулю. И наоборот если проводник перпендикулярен магнитных силовых линий, то сила, воздействующая на него, достигнет максимального значения.

Сила, оказывающая воздействие на проводник с током, зависит и от магнитной индукции. Чем плотнее силовые линии, тем больше сила, действующая на проводник с током. Поэтому, мы можем действие магнитного поля на проводник с током выразить следующим определением:

Сила, действующая на проводник с током, прямо пропорциональна магнитной индукции, силе тока и длине проекции, находящейся в магнитном поле, на плоскость, перпендикулярную магнитному потоку.

Необходимо добавить, что действие магнитного поля на ток не зависит ни от материала проводника, ни от сечения. Действие магнитного поля проявляется даже при отсутствии проводника, пропуская, между полюсами постоянного магнита поток быстро идущих электронов. Действие магнитного поля на ток нашло широкое применение в науке и технике. На этих принципах основано устройство электродвигателей, магнитоэлектрических приборов для измерения напряжения и силы тока, магнетронов, катодно-лучевых трубок и т. д. Действием магнитного поля применяется для измерения массы и заряда электрона и даже при изучении строения вещества.

 

 

17 Электромагнитная индукция. Электродвижущая сила, индуктированная в проводнике. Правило правой руки, правило Ленца.

Существует и другое очень важное явление, в известном смысле обратное явлению магнитной индукции: при движении замкнутого проводника в маг­нитном поле в нем по­является электрический ток. Это явление называется электромагнитной индукцией.

при пересечении про­водником магнитного поля в проводнике возникает ЭДС, направление которой зависит от направления движения про­водника. Эта ЭДС называется индуктированной ЭДС или ЭДС индукции, то есть наведение ЭДС в проводнике и есть не что иное, как явление электромагнитной индукции (не следует сме­шивать с магнитной индукцией!).

Наведение ЭДС индукции при движении проводника в магнитном поле объясняется следующим образом. При движе­нии проводника вместе с ним движутся и свободные электроны, находящиеся в нем. При изучении магнитной индукции мы узнали, что на электрические заряды, движущиеся в магнитном поле, дей­ствует сила в направлении, перпендикулярном направлению магнитного потока. Поэтому при движении электронов вместе с проводником, пересекающим магнитные силовые линии, на электроны будут действо­вать силы, заставляющие их перемещаться вдоль проводника, что и приводит к возникновению электрического тока в нем.

Явление электромагнитной индукции имеет большое значе­ние в электро- и радиотехнике, поэтому мы остановимся на нем несколько подробнее.

Попробуем производить перемещение проводника в магнитном поле с различной скоростью. При этом мы заметим, что стрелка гальванометра будет отклоняться тем больше, чем быстрее наш проводник пересекает магнитное поле. При очень медленном перемещении проводника в нем совершенно не воз­никает тока или, говоря точнее, ток будет настолько мал, что наш гальванометр не в состоянии его обнаружить.

Далее обратим внимание на то обстоятельство, что, вдви­гая проводник в пространство между полюсами магнита, мы тем самым увеличиваем число магнитных силовых линий, охва­тываемых замкнутым контуром проводника, а при обратном перемещении проводника уменьшаем число этих линий, или, другими словами, в первом случае магнитный поток, охваты­ваемый нашим замкнутым контуром, увеличивается, а во вто­ром случае уменьшается. С этой точки зрения возникновение индукционного тока в замкнутом проводящем контуре мы мо­жем объяснить как результат изменения величины магнитного потока внутри контура; большие или меньшие отклонения стрелки при разных скоростях движения проводника свиде­тельствуют о том, что ЭДС индукции зависит от скорости изменения магнитного потока внутри контура.

При быстром возрастании (или убывании) магнитного по­тока внутри контура в нем наводится большая ЭДС индук­ции, а при медленном возрастании (или убывании) — малая.

Практически направление индукцион­ного тока определяется по правилу правой руки (рисунок 2).

Правило правой руки состоит в том, что, если по­местить правую руку в магнитное поле так, чтобы магнитные силовые линии входили в ладонь, а большой палец указывал направле­ние движения проводника, то остальные четыре пальца покажут направление ин­дукционного тока, возникающего в провод­нике.

В сжатой форме правило Ленца можно сформулировать так:

возникающий в замкнутом проводнике индукционный ток имеет такое направление, чтобы препятствовать изменению потока магнитной индукции, которое его вызывает.

То есть индукционный ток создает через площадь, ограниченную контуром собственный поток магнитной индукции, компенсирующий изменение потока магнитной индукции, которое его вызывает

 

18 Самоиндукция и индуктивность.

В момент включения постоянного тока (рисунок 1) вокруг проводника образуется магнитное силовое поле. В первые мгновения после включения тока значительная часть энергии источника тока затрачивается на создание этого магнитного поля и лишь незначительная часть — на преодоление сопро­тивления проводника, вернее на нагревание током проводника. Поэтому в момент замыкания цепи ток не сразу достигает предельной своей величины. Предельная сила тока устанавли­вается в цепи лишь после окончания процесса образования вокруг проводника магнитного поля (рисунок 2).

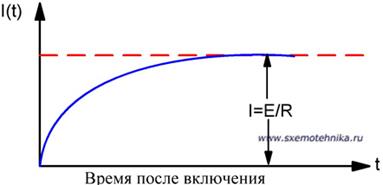
Если не разрывая замкнутой цепи, выключить из нее ис­точник тока, то ток в цепи прекратится не сразу, а будет про­текать в ней, еще некоторое время уменьшаясь постепенно (рисунок 3) до тех пор, пока не исчезнет магнитное поле во­круг проводника, т. е. пока не израсходуется весь запас энер­гии, заключенной в магнитном поле.

 

ИНДУКТИВНОСТЬ в электродинамике (коэффициент самоиндукции) (от лат. inductio - наведение, побуждение) - параметр электрич. цепи, определяющий величину эдс самоиндукции, наводимой в цепи при изменении протекающего по ней тока и (или) при её деформации

Итак, магнитное поле является носителем энергии. Оно на­копляет в себе энергию при включении источника постоянного тока и отдает ее обратно в цепь после выключения источника тока. Энергия магнитного поля, таким образом, имеет много общего с кинетической энергией движущегося предмета. Маг­нитное поле служит причиной «инерции» электрического тока.

Мы знаем, что всякий раз, когда изменяется магнитный поток, пронизывающий площадь, ограниченную замкнутой электрической цепью, в этой цепи появляется ЭДС индукции.

Кроме того, нам известно, что всякое изменение силы тока в цепи влечет за собой изменение числа магнитных силовых линий, охватываемых этой цепью. Если замкнутая цепь непо­движна, то число магнитных силовых линий, пронизывающих данную площадь, может измениться только тогда, когда но­вые линии войдут снаружи в пределы этой площади или когда существующие уже линии выйдут за пределы этой площади. И в том и в другом случае магнитные силовые линии при своем движении должны пересечь проводник. Пересекая про­водник, магнитные силовые линии наводят в нем ЭДС ин­дукции. Но так как в этом случае проводник индуктирует ЭДС в самом себе, то эта ЭДС называется ЭДС самоиндукции.

При включении источника постоянного тока в какую-либо замкнутую цепь площадь, ограниченную этой цепью, начинают пронизывать извне магнитные силовые линии. Каждая магнит­ная силовая линия, приходящая извне, пересекая проводник, наводит в нем ЭДС самоиндукции.

Индуктивностью называется величина, которая равна отношению магнитного потока, проходящего по всем виткам контура к силе тока: L = N х F: I. Как найти индуктивность Формула, которая является простейшей для нахождения величины, следующая: L = F: I, где F – магнитный поток, I – ток в контуре. Через индуктивность можно выразить ЭДС самоиндукции: Ei = -L х dI: dt. Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду. Переменная индуктивность дает возможность найти и энергию магнитного поля: W = L I2: 2

 

19 Взаимоиндукция и взаимная индуктивность

Если две катушки находятся на некотором расстоянии друг от друга и по одной из них К ₁ проходит изменяющийся ток, то часть магнитного потока, возбуждаемого этим током, пронизывает (пересекает) витки второй катушки К ₂ и в ней возникает э. д. с., называемая э. д. с. взаимоиндукции (рис. 47).

Под действием э. д. с. взаимоиндукции в замкнутой цепи второй катушки возникает электрический ток взаимоиндукции. Он вызывает появление магнитного поля, которое пронизывает витки первой катушки, в результате чего в ней также возникает э. д. с. взаимоиндукции. Такое явление называется взаимоиндукцией.
Величина э. д. с. взаимоиндукции, возникающей во второй катушке, зависит от размеров, расположения катушек, магнитной проницаемости их сердечника, а также от скорости изменения силы тока 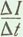в первой катушке. Эту зависимость можно выразить формулой

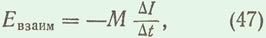
где Δ I — изменение силы тока (а) за время Δ t, сек;
М — величина, зависящая от размеров катушек, их расположения и магнитной проницаемости среды между катушками. Она называется взаимной индуктивностью и измеряется в генри (гн).
Знак минус в этой формуле показывает, что э. д. с. взаимоиндукции противодействует причине, вызывающей ее.
Взаимной индуктивностью в 1 гн обладают две цепи в том случае, если в одной из них возникает э. д. с. взаимоиндукции в 1 в при равномерном изменении тока в другой цепи со скоростью 1 а в 1 сек.
На использовании явления взаимоиндукции основано действие трансформаторов.

 

20 Измерительные приборы. Классификация приборов и их условное обозначение

 

⇐ Предыдущая12345

Поделиться:

Воспользуйтесь поиском по сайту: