 |
Познавательные универсальные учебные действия
|
|
|
|
Диагностика особенностей развития поискового планирования (методика А.З.Зака)
Время проведения: декабрь
Цель: выявление сформированности действия поискового планирования как умения разрабатывать программу выполнения действий для достижения поставленной цели.
Оцениваемые УУД: регулятивные действия планирования и контроля, логические действия анализа, синтеза, установления аналогий.
Возраст: ступень начального обучения (9-11 лет).
Форма и ситуация оценивания: групповая и индивидуальная форма.
Далеко не всегда имеет место разработка программы действий.
В этом случае каждое действие планируется и сразу же выполняется. Поэтому
последующие действия планируются только после выполнения предыдущих.
Такая форма планирования квалифицируется как последовательно-частичное
планирование. В других случаях разрабатываются и сопоставляются разные варианты всей последовательности требуемых действий. При этом предыдущие действия выполняются лишь после того, как будут намечены все последующие действия. Такая форма планирования квалифицируется как предварительно-целостное планирование.
Для диагностики поискового планирования можно использовать тип задач, в которых для достижения результата требуется выполнить ряд действий. В этом случае можно будет различить уровни развития планирования у детей в зависимости от того, какое количество действий (до выполнения) способен наметить ребенок.
К такому типу относятся задачи «слон — ладья». Смысл их заключается в том, чтобы некоторое расположение объектов преобразовать в другое за определенное количество действий по определенным правилам.
Например, расположение цифр в квадрате «А» нужно преобразовать в расположение тех же цифр, указанное в квадрате «Б» за два действия по следующему правилу: любая цифра за одно действие может переместиться прямо или наискось только в соседнюю свободную клетку:
|
|
|

В данной задаче первое действие состоит в перемещении по прямой (ходом шахматной фигуры «ладья») цифры «1», а второе действие связано с перемещением в соседнюю свободную клетку наискось (ходом шахматной фигуры «слон») цифры «2».
Усложнение условий планирования при решении таких задач связано как с увеличении числа требуемых операций, так и с возрастанием числа клеток и числа перемещающихся объектов.
Групповое диагностическое исследование для определения различий в планировании у младших школьников строится следующим образом.
Учитель, проводящий диагностическое занятие, приходит в класс с
комплектом бланков и с чистыми листами бумаги для записи решения задач:
на этих листах каждый ребенок пишет свою фамилию и ставит дату
проведения занятия.
Пока дети подписывают чистые листы, психолог чертит на классной доске
два четырехклеточных квадрата:

Детям говорится: «Сегодня мы будем решать интересные задачи.
Посмотрите на эти два квадрата. Каждая клетка в квадрате имеет свое
название, которое состоит из буквы и цифры. Эта клетка (следует указать
нижнюю левую клетку) называется А1, а эта клетка (указывается правая
нижняя) называется Б1, а эти две клетки (верхние две клетки квадрата)
называются А2 и Б2».
«Теперь решим такую интересную задачу. Сначала три фигурки — круг,
треугольник и ромб — были в таких клетках», — психолог рисует указанные
фигурки:
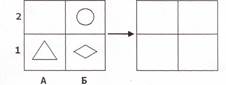
«А потом фигурки поменяли свои места и оказались в других клетках», — психолог рисует фигурки в правом квадрате:

«Нам нужно угадать, узнать, какие два действия, два перемещения сделали фигурки, чтобы попасть в другие клетки. Чтобы решить эту задачу, нужно знать правило: любая фигурка может перемещаться только в свободную соседнюю клетку прямо или наискось. Кто скажет, какое было первое перемещение, какая фигурка первая передвинулась в свободную клетку?... Правильно, первое действие сделал ромб: из клетки Б1 он передвинулся наискось в клетку А2. Запишем это действие, используя названия клеток:
|
|
|

А какое будет второе действие?. Правильно, второе действие выполнил круг. Он передвинулся из клетки Б2 прямо в клетку Б1. Запишем второе действие рядом с первым:
1)Б1 ->вА2; 2)Б2-*Б1.
Вот так решаются задачи на перемещение фигурок из одних клеток в другие.
Сейчас я раздам бланки с условиями задач, которые вы будете сегодня
решать», — учитель раздает бланки, в каждом из которых даны 12 задач.
«Давайте посмотрим на лист с задачами. На самом верху есть задачи №1 и
№2. В них нужно отгадать, найти два действия. Затем идут задачи №3 и №4 в них нужно найти 3 действия. Далее в задачах №5 и №6 нужно найти 4
действия, в задачах №7 и №8 нужно найти 5 действий, в задачах №9 и №10
6 действий, в задачах №11 и №12 — 7 действий.
7. Теперь попробуйте сами решить задачу №1 в два действия. Помните наше
правило: фигурки перемещаются прямо и наискось в свободную клетку.
Подумайте, как перемещались фигурки: какая фигурка передвинулась
первой, какая передвинулась второй. Потом запишите эти два действия также, как мы это делали на доске: сначала номер задачи, потом первое действие и второе».
Дети решают задачу №1, учитель проходит по рядам и контролирует
правильность записи решения.
«Давайте проверим теперь решение задачи №1», — учитель на доске
рисует условие задачи № 1:
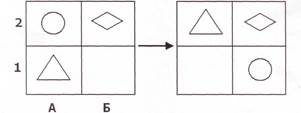
Кто скажет решение? Верно, первое действие сделал круг, второе — треугольник: №1.
1) А2 —> Б1; 2) А1 —> А2.
10. Теперь решайте задачу №2, — в ней тоже нужно найти 2 действия». Дети
решают задачу, психолог контролирует работу детей.
11. «Давайте проверим решение задачи №2», — учитель рисует на доске
условие задачи:
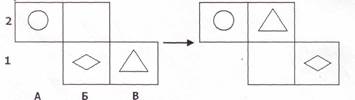
12.«Кто скажет решение этой задачи? Верно, первое действие: треугольник переместился из клетки Б1 в В1. Запишем эти два действия:
№2. 1)В1 →Б2; 2)Б1→ В1.
13.Вот так решаются и записываются действия в наших задачах. Теперь сами и уже без проверки решайте все задачи подряд: №№3, 4 и т.д., кто сколько успеет. Только помните правило: фигурки перемещаются прямо и наискось в соседнюю свободную клетку. На бланке с задачами ничего писать нельзя: ни точки, ни линии. Нужно просто смотреть на условия задач и думать, какие перемещения сделали фигурки из одних клеток в другие». Последнее требование, — не касаться бланка ручкой или карандашом, — принципиально важно для диагностики планирования, поскольку проверяется развитие способности действовать «в уме», в мысленном плане, в представлении, т.е. без фиксирования промежуточных результатов на бумаге, например, в виде точки на клетке с той или иной фигуркой или проведения линий, указывающих на возможные перемещения фигурок.
|
|
|
14.На инструктирование детей отводится (в зависимости от возраста) 10-15 минут, а на самостоятельное решение задач №№ 3 - 12 должно быть потрачено ровно 20 минут. По истечении этого времени бланки и листы с ответами (кто сколько успел решить) собираются.
Критерии и уровни оценки планирования:
1. протяженность последовательности действий (количество действий), спланированная ребенком.
Обработка результатов
Результаты решения задач, находящиеся на листах бумаги с фамилиями детей, можно обрабатывать, сверяясь с ключом, где представлены правильные действия к каждой задаче.
Диагностическое задание включает задачи двух видов. К первому относятся задачи, решение которых может быть достигнуто с помощью частичного планирования, — это задачи №№ 1 и 2, — поскольку выбор первого действия однозначен, и его наметка и выполнение не связаны с наметкой и выполнением второго действия.
Ко второму виду относятся задачи, решение которых предполагает осуществление целостного планирования, это задачи № 3 - 12, поскольку выбор первого действия неоднозначен. Последнее означает, что правильный выбор первого действия влияет на возможность решить задачу за требуемое число действий, и поэтому наметку первого действия следует проводить одновременно с наметкой всех остальных действий.
|
|
|
Уровни планирования:
1 - успешное решение задач № 3 и №4
2 – успешное решение задач №5 и №6
3 – успешное решение задач №6 и №7
4 – успешное решение задач №9 и № 10
5 – успешное решение задач № 11 и № 12
В целом, таким образом, проведение группового диагностического занятия с детьми 7-10 лет позволяет выделить тех, кто обладает либо только частным планированием (при решении лишь двух первых задач), либо разными уровнями развития целостного планирования, — при успешном решении, соответственно, задач №№ 1 - 4; 1 - 6; 1 - 8; 1 - 10; 1 - 12.
Сформированность универсального действия общего приема решения задач (по А.Р.Лурия, Л.С.Цветковой)
Время проведения: май
Цель: выявление сформированности общего приема решения залач.
Оцениваемые УУД: универсальное познавательное действие общего приема решения задач; логические действия.
Возраст: ступень начальной школы.
Известно, что процесс решения текстовых арифметических задач имеет сложное психологическое строение. Он начинается с анализа условия, в котором дана сформулированная в задаче цель, затем выделяются существенные связи, указанные в условии, и создается схема решения; после этого отыскиваются операции, необходимые для осуществления найденной схемы, и, наконец, полученный результат сличается с исходным условием задачи. Достижение нужного эффекта возможно лишь при постоянном контроле за выполняемыми операциями.
Трудности в решении задач учащимися в большинстве случаев связаны с недостаточно тщательным и планомерным анализом условий, с бесконтрольным построением неадекватных гипотез, с неоправданным применением стереотипных способов решения, которые нередко подменяют полноценный поиск нужной программы. Причиной ошибок нередко оказывается и недостаточное внимание к сличению хода решения с исходными условиями задачи и лишь иногда — затруднения в вычислениях.
Решение задачи является наиболее четко и полно выраженным интеллектуальной деятельностью. Внимательный анализ процесса решения задачи в различных условиях дает возможность описать структуру изменений этого процесса и выделить различные факторы, определяющие становление полноценной интеллектуальной деятельности.
Таким образом, анализ решения относительно элементарных арифметических задач является адекватным методом, позволяющим получить достаточно четкую информацию о структуре и особенностях интеллектуальной деятельности обучающихся и ее изменениях в ходе обучения.
А.Р.Лурия и Л.С.Цветкова предложили известный набор задач с постепенно усложняющейся структурой, который дает возможность последовательного изучения интеллектуальных процессов обучающихся.
|
|
|
Наиболее элементарную группу составляют простые задачи, в которых условие однозначно определяет алгоритм решения, типа a + b = х или a – b = х:
У Маши 5 яблок, a y Пети 4 яблока. Сколько яблок у них обоих?
Коля собрал 9 грибов, а Маша — на 4 гриба меньше, чем Коля. Сколько грибов собрала Маша?
В мастерскую привезли 47 сосновых и липовых досок. Липовых было 5 досок. Сколько привезли в мастерскую сосновых досок?
Простые инвертированные задачи типа a – х = a или x – a = b, существенно отличающиеся от задач первой группы своей психологической структурой:
У мальчика было 12 яблок; часть из них он отдал. У него осталось 8 яблок. Сколько яблок он отдал?
На дереве сидели птички. 3 птички улетели; остапось 5 птичек. Сколько птичек сидело на дереве?
Составные задачи, в которых само условие не определяет возможный ход решения, типа a + (a + b) = x или a + (a – b) =x:
У Маши 5 яблок, a y Кати на 2 яблока больше (меньше). Сколько яблок у них обеих?
У Пети 3 яблока, a y Васи — в 2 раза больше. Сколько яблок у них обоих?
Сложные составные задачи, алгоритм решения которых распадается на значительное число последовательных операций, каждая из которых вытекает из предыдущей, типа a + (a + b) + [(a + b) - c] = x или x = a ´ b; y = x/n; z = x – y:
Сын собрал 15 грибов. Отец собрал на 25 грибов больше, чем сын. Мать собрала на 5 грибов меныие отца. Сколько всего грибов собрала вся семья?
У фермера было 20 га земли. С каждого гектара он снял по 3 тонны зерна. 1/2 зерна он продал. Сколько зерна осталось у фермера?
Сложные задачи с инвертированным ходом действий, одна из основных частей которых остается неизвестной и должна быть получена путем специальной серии операций и котрые включают в свой состав звено с инвертированным ходом действий, типа a + b = x; x – m = y; y – b = z:
Сыну 5 лет. Через 15 лет отец будет в 3 раза старше сына. Сколько лет отцу сейчас?
Задачи на сличение двух уравнений и выделение специальной вспомогательной операции, являющейся исходной для правильного решения задачи, типа x + y = а; nx + y = b или x + у + z = а; x + у - b; у + z – b:
Одна ручка и один букварь стоят 37 рублей. Две ручки и один букварь стоят 49 рублей. Сколько стоит отдельно одна ручка и один букварь?
Три мальчика поймали 11 кг рыбы. Улов первого и второго был 7 кг; улов второго и третьего — 6 кг. Сколько рыбы поймал каждый из мальчиков?
Конфликтные задачи, в которых алгоритм решения вступает в конфликт с каким-либо хорошо упроченным стереотипом решающего, и правильное решение которых возможно при условии преодоления этого стереотипа:
Отцу 49 лет. Он старше сына на 20 лет. Сколько лет им обоим?
Рабочий получал в получку 1200 рублей и отдавал жене 700 рублей. В сегодняшнюю получку он отдал жене на 100 рублей больше, чем всегда. Сколько денег у него осталось?
Длина карандаша 15 см; Тень длиннее карандаша на 45 см. Во сколько раз тень длиннее карандаша?
Типовые задачи, решение которых невозможно без применения какого-либо специального приема, носящего чисто вспомогательный характер. Это задачи на прямое (обратное) приведение к единице, на разность, на части, на пропорциональное деление:
5 фломастеров стоят 30 рублей. Купили 8 таких фломастеров. Сколько денег заплатили?
Купили кисточек на 40 рублей. Сколько кисточек купили, если известно, что 3 таких кисточки стоят 24 рубля?
На двух полках было 18 книг. На одной из них было на 2 книги больше. Сколько книг было на каждой полке?
Пузырёк с пробкой стоят 11 копеек. Пузырёк на 10 копеек дороже пробки. Сколько стоит пузырёк и сколько стоит пробка?
В двух карманах лежало 27 копеек. В левом кармане было в 8 раз больше денег, чем в другом. Сколько денег было в каждом кармане?
Трое подростков получили за посадку деревьев 2500 рублей. Первый посадил 75 деревьев, второй — на 45 больше первого, а третий — на 65 меньше второго. Сколько денег получил каждый?
Усложненные типовые задачи типа [(x – a) + (x – b) + m = x]; [nx + ky = b; x – y = c]:
Двое мальчиков хотели купить книгу. Одному не хватало для ее покупки 7 рублей, другому не хватало 5 рублей. Они сложили свои деньги, но им все равно не хватило 3 рублей. Сколько стоит книга?
По двору бегали куры и кролики. Сколько было кур, если известно, что кроликов было на 6 больше, а у всех вместе было 66 лап?
Все задачи (в зависимости от ступени обучения испытуемых) предлагаются для устного решения арифметическим (не алгебраическим) способом. Допускаются записи плана (хода) решения, вычислений, графический анализ условия. Учащийся должен рассказать, как он решал задачу, доказать, что полученный ответ правилен.
Существенное место в исследовании особенностей развития интеллектуальной деятельности имеет анализ того, как испытуемый приступает к решению задачи, и в каком виде строится у него ориентировочная основа деятельности. Необходимо обратить внимание на то, как учащийся составляет план или общую схему решения задачи, как составление предварительного плана относится к дальнейшему ходу ее решения. Кроме того, важным является анализ осознания проделанного пути и коррекции допущенных ошибок. Также достаточно важным является фиксация обучающей помощи при затруднениях уроков учащегося и анализ того, как он пользуется помощью, насколько продуктивно взаимодействует со взрослым.
Методика «Нахождение схем к задачам» (по Рябинкиной)
Время проведения: апрель
Цель: методика позволяет определить умение ученика выделять тип задачи и способ ее решения.
Оцениваемые УУД: моделирование, познавательные логические и знаково-символические действия, регулятивное действие оценивания и планирования; сформированность учебно-познавательных мотивов (действие смыслообразования).
Возраст: ступень начального образования (7-9 лет).
Форма и ситуация оценивания: фронтальный опрос или индивидуальная работа с детьми.
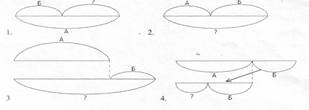
Инструкция: «Найди правильную схему к каждой задаче. В схемах числа обозначены буквами». Предлагаются следующие задачи.
Миша сделал 6 флажков, а Коля на 3 флажка больше. Сколько флажков
сделал Коля?
На одной полке 4 книги, а на другой на 7 книг больше. Сколько книг на двух
полках?
На одной остановке из автобуса вышло 5 человек, а на другой вышли 4
человека. Сколько человек вышли из автобуса на двух остановках?
На велогонке стартовали 10 спортсменов. Во время соревнования со старта
сошли 3 спортсмена. Сколько велосипедистов пришли к финишу?
В первом альбоме 12 марок, во втором — 8 марок. Сколько марок в двух
альбомах?
Маша нашла 7 лисичек, а Таня — на 3 лисички больше. Сколько грибов
нашла Таня?
У зайчика было 11 морковок. Он съел 5 морковок утром. Сколько морковок
осталось у зайчика на обед?
На первой клумбе росло 5 тюльпанов, на второй — на 4 тюльпана больше,
чем на первой. Сколько тюльпанов росло на двух клумбах?
У Лены 15 тетрадей. Она отдала 3 тетради брату, и у них стало тетрадей
поровну. Сколько тетрадей было у брата?
В первом гараже было 8 машин. Когда из него во второй гараж переехали две машины, в гаражах стало машин поровну. Сколько машин было во втором гараже?
|
|
|


