Главная | Обратная связь | Поможем написать вашу работу!
 МегаЛекции

Условные обозначения и символы




Задания

По ИНЖЕНЕРНОЙ ГРАФИКЕ

(Часть 1)

Методические указания

к выполнению индивидуальных заданий

для студентов по направлению подготовки

1003 «Судовождение и энергетика судов»

дневной и заочной форм обучения

 

 

Севастополь

 

УДК 515 (075)

Задания по инженерной графике (Часть 1): Методические указания / Сост. А.Ф. Медведь, В.Г. Середа. – Севастополь: Изд-во СевНТУ, 2006. – 36 с.

 

 

Методические указания содержат минимальный объем индивидуальных заданий, самостоятельное выполнение которых способствует практическому закреплению знаний раздела дисциплины «Инженерная графика».

 

Методические указания утверждены на заседании кафедры начертательной геометрии и графики, протокол

№ 1 от 23.08.2005 г.

 

Допущено учебно-методическим центром СевНТУ в качестве методических указаний.

 

Рецензент: Смагин В.В. канд. техн. наук, доцент кафедры начертательной геометрии и графики

 

 

Содержание

ВВЕДЕНИЕ…………………..………………………………...  
1. Условные обозначения и символы………..……………….  
2. Индивидуальные задания…………………………………..  
2.1. Геометрические построения………….……………….…  
2.2. Моделирование группы геометрических тел…………...  
2.3. Моделирование структуры геометрических объектов…  
2.4. Моделирование метрических характеристик объектов..  
2.5. Моделирование сечений геометрических тел…………..  
2.6. Моделирование линии пересечения поверхностей……..  
2.7. Моделирование сложных геометрических форм……….  
2.8. Моделирование разверток поверхностей….....................  
заключение………………………………………………...  
Библиографический список………………………...  

 

ВВЕДЕНИЕ

Учебный процесс по инженерной графике включает следующие формы обучения.

Лекции. На лекциях студенты получают основную информацию по теоретическим основам курса, знакомятся со способами решения задач.

Самостоятельная работа студентов. Теоретический материал углубленно изучается по рекомендованным учебникам, пособиям и методическим указаниям. Закрепляется решением задач, помещенных в методических указаниях. Выполняются индивидуальные расчетно – графические работы.

Практические занятия. Включают следующие этапы работы:

- краткий обзор по теме занятия;

- проверка задач и заданий, самостоятельно выполненных студентами;

- программированный контроль знаний по теме занятия;

- решение типовых задач или выполнение расчетно – графического задания.

Индивудуальные консультации. Проводятся по расписанию кафедры.

Экзамен (дифференцированный зачет). Поводится в соответствии с рабочим планом. К экзамену допускаются студенты, самостоятельно решившие задачи и сдавшие расчетно – графические задания.

Вариант для выполнения задания определяется как остаток от деления трех последних цифр номера зачетной книжки на 30. Например, если номер зачетной книжки студента 030216, то он выполняет 6-й вариант, так как при делении 216 на 30 в остатке будет 6 (если остаток равен нулю, то принимается 30 вариант).

Условные обозначения и символы

Точка в пространстве - прописными буквами латинского алфавита: А,В,С, D, Е…или цифрами: 1,2,3,4,…

Прямые и кривые линии - строчными буквами латинского алфавита: а, в, с, d….. Линии уровня - буквами: горизонтали - h, фронтали - f, профильные прямые - p.

- направляющие линии (соответственно прямые и кривые) поверхности;

- образующие линии (соответственно прямые и кривые) поверхности.

Плоскости и поверхности - прописными буквами греческого алфавита: S, U, Ф, D, Г, Т.

Плоские углы - строчными греческими буквами: a, b, g, d,…

Плоскости проекций – греческой буквой П с подстрочными индексами 1,2,3,4,5… Основные плоскости проекций: П1 - горизонтальная, П2 - фронтальная, П3 - профильная.

Проекции точек, прямых, плоскостей, поверхностей, углов - теми же буквами, что и в пространстве, с добавлением подстрочного индекса соответствующей плоскости проекций: А1, а 1, S1,…

Натуральная система координат - ОXYZ.

Оси проекций на чертеже - X12, Y13, Z23, начало координат О.

Центры и направления проецирования - S, U.

При замене плоскостей проекций новая ось - буквой с соответствующим индексом: X14, Y25 и т.д.
Новое положение точки после одного вращения или перемеще-

 
 


ния 1, после двух - 1.

Плоскость аксонометрических проекций обозначается буквой П со знаком штрих - П¢.

Аксонометрические проекции точек, прямых, плоскостей и углов обозначаются теми же буквами со штрихом - А¢, а ¢, S¢, b¢,….

Вторичные проекции имеют внизу индекс прямоугольных проекций, в вверху - штрих: А1¢, а 1¢, a1¢,….

Аксонометрические оси обозначаются буквами Х¢,U¢, Z¢, начало координат буквой О.

Принятые символы:

º - тождественность; Ì - лежит на;

É - проходит через; çç - параллельность;
^ - перпендикулярность; Ç - пересечение;
È - соединение; - касание;

- скрещивание; / - не;

 

Ù - и; Ú - или;

= - равно, есть; Þ - если…, то;

? - построить, определить;! - строим, определяем.

Индивидуальные задания

Изучение курса «Инженерная графика» сопровождается выполнением студентами расчетно-графических заданий, способствующих закреплению теоретического материала курса, увязыванию теории с практическими задачами, освоению графических приемов решения задач и развитию пространственного представления.

К выполнению и оформлению заданий предъявляются следующие требования:

- каждое задание является индивидуальным и может содержать несколько задач;

- каждое задание выполняется карандашом на листе формата А3(420х297);

- обозначение чертежей выполняется по следующей схеме: СНТУ.101300.001, где СНТУ - сокращенное наименование вуза; 1 - номер задания; 013 - номер варианта; 001 - номер листа в задании;

- условия задач, все геометрические построения выполняют с помощью чертежных инструментов, карандашом Т(Н), сначала тонкими линиями (0,2 мм), а затем линии видимого контура обводят карандашом М(В) сплошной линией толщиной 0,6…0,8 мм, линии невидимого контура - штриховой 0,3…0,4 мм, все остальные - тонкой линией 0,2…0,4 мм;

- надписи на поле чертежа и буквенные обозначения выполняются шрифтом типа Б с наклоном согласно ГОСТ 2.304-81. Размер шрифта - 5;

- над каждой задачей проставляется ее порядковый номер;

- наглядные изображения строятся в прямоугольной изометрии или фронтальной диметрии согласно ГОСТ 2.317- 69.

Прежде, чем приступить к выполнению очередного задания необходимо:

- изучить материал соответствующей темы по конспекту лекций или учебнику и подкрепить изученный раздел самостоятельным решением задач;

- уяснить пространственное расположение исходных геометрических элементов в задаче;

- наметить последовательность пространственных операций, которые необходимо выполнить для решения задачи;

- выполнить все графические построения и нанести буквенные обозначения.

При выполнении каждого задания следует придерживаться такой последовательности:

- наметить рамку чертежа по формату;

- выполнить основную надпись согласно ГОСТ 2.104-68;

- наметить место для каждой задачи;

- перенести на лист чертежи условий задач;

- выполнить графическое решение задач;

- проверить решение каждой задачи;

- произвести обводку чертежа, рамки и основной надписи;

- нанести буквенные обозначения на поле чертежа и текст в основной надписи.

Выполненные и подписанные преподавателем чертежи брошюруются в альбом с оформлением титульного листа. Образец титульного листа приведен на рисунке 1.

Студенты заочной формы обучения представляют выполненные графические работы на рецензирование за месяц до начала установочной сессии.

2.1. Геометрические построения

Цель задания - усвоение основных правил оформления чертежей и овладения техникой геометрических построений.

Рекомендации к выполнению задания: Исходные данные для выполнения задания выбираются по вариантам в таблицах 1, 2, 3 и 4.

Задание выполняется на листе формата А3 (420х297). Образец задания приведен на рисунке 2.

На листе «Геометрические построения» вычерчивают изображение прокатного профиля, крюка, а также коробовые (овал) и лекальные (парабола, гипербола или эллипс) кривые линии.

Рекомендуется следующий порядок выполнения задания:

1. Наметить рамку по формату чертежа и выполнить основную надпись.

3. Наметить место каждого изображения.

Масштаб каждого изображения выбирается исходя из того, что примерно 75% поля чертежа должно быть занято изображениями. Например, масштаб сечения профиля выбрать с учетом того, чтобы полка профиля в масштабе была в пределах 60…125 мм, а при вычерчивании высоты профиля – использовать линии обрыва. Масштаб крюка выбрать из условия, чтобы сумма R1+b была в пределах (160…270) мм. Масштаб кривых выбирать после

вычерчивания в тонких линиях двух предыдущих изображений.

4. Выполнить построения каждого изображения в тонких линиях. Построение овала выполняют в соответствии с пунктом 3.1 [2]. Построение лекальных

 

кривых линий выполняют по рекомендациям приведенным в пунктах 3.2, 3.3 или 3.4 [2] соответственно. Построение сечения прокатного профиля выполняют по рекомендациям приведенным в пунктах 4.1 и 4.2 [2].

5. Проверить построения.

6.Выполнить обводку чертежа, рамки и граф основной надписи.

 

Рисунок 1

 

Рисунок 2

 

Таблица 1 - Перечень изображений по вариантам заданий

№ варианта Наименование изображения
       
  Швеллер Крюк1 Овал Эллипс
  Двутавр Крюк2 Овал Парабола
  Швеллер Крюк1 Овал Гипербола
  Двутавр Крюк2 Овал Эллипс
  Швеллер Крюк1 Овал Парабола
  Двутавр Крюк2 Овал Гипербола
  Швеллер Крюк1 Овал Эллипс
  Двутавр Крюк2 Овал Парабола
  Швеллер Крюк1 Овал Гипербола
  Двутавр Крюк2 Овал Эллипс
  Швеллер Крюк1 Овал Парабола
  Двутавр Крюк2 Овал Гипербола
  Швеллер Крюк1 Овал Эллипс
  Двутавр Крюк2 Овал Парабола
  Швеллер Крюк1 Овал Гипербола
  Двутавр Крюк2 Овал Эллипс
  Швеллер Крюк1 Овал Парабола
  Двутавр Крюк2 Овал Гипербола
  Швеллер Крюк1 Овал Эллипс
  Двутавр Крюк2 Овал Парабола
  Швеллер Крюк1 Овал Гипербола
  Двутавр Крюк2 Овал Эллипс
  Швеллер Крюк1 Овал Парабола
  Двутавр Крюк2 Овал Гипербола
  Швеллер Крюк1 Овал Эллипс
  Двутавр Крюк2 Овал Парабола
  Швеллер Крюк1 Овал Гипербола
  Двутавр Крюк2 Овал Эллипс
  Швеллер Крюк1 Овал Парабола
  Двутавр Крюк2 Овал Гипербола

 

Таблица 2 – Исходные данные

  Швеллер Двутавр  

 

 

Крюк 1

     Крюк 2

 

Продолжение таблицы 2

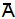
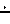
      AB=a; CD=b   Овал         AB=a; CD=b   Эллипс
      Парабола         Гипербола

 

 
 
Таблица 3 - Размеры изображений, в мм
№ варианта Наименование изображения
Швеллер, двутавр Коробовые и лекальные кривые
№ профиля   h   b     s   t   R   r   a   b   c
        4,5 7,6 3,0 3,5     -
        4,5 7,2 7,0 2,5     -
        4,8 7,8 7,5 3,0      
        4,8 7,3 7,5 3,0     -
        4,9 8,1 8,0 4,5     -
        4,9 7,5 8,0 3,0      
        5,0 8,4 8,5 3,5     -
        5,0 7,8 8,5 3,5     -
        5,1 8,7 9,0 3,5      
        5,1 8,1 9,0 3,5     -
        5,2 9,0 9,5 4,0     -
        5,2 8,4 9,5 4,0      
        5,4 9,5 10,0 4,0     -
        5,4 8,7 10,0 4,0     -
        5,6 10,0 10,5 4,0      
        5,6 9,5 10,5 4,0     -
        6,0 10,5 11,0 4,5     -
        6,0 9,8 11,0 4,5      
        6,5 11,0 12,0 5,0     -
        6,5 10,2 12,0 5,0     -
        7,0 11,7 13,o 5,0      
        7,0 11,2 13,0 5,0     -
        7,5 12,6 14,0 6,0     -
        7,5 12,3 14,0 6,0      
        8.0 13,5 15,0 6,0     -
        8,3 13,0 15,0 6,0     -
        5,4 9,5 10,0 4,0      
        9,0 14,2 16,0 7,0     -
        5,6 10,0 10,5 4,0     -
        10,0 15,2 17,0 7,0      

 

 

 


Таблица 4 - Размеры крюка, в мм

№вар   а   b   h   m   s   D   d   R1   R2   R3   n
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       
                       

 

 

2.2. Моделирование группы геометрических тел

Целевое назначение. Закрепление знаний студентов по кодированию и декодированию геометрической информации на чертеже, т.е. умению изображать и узнавать на чертеже простейшие геометрические объекты (тела), а также строить проекции точек и линий, принадлежащих поверхностям этих тел.

Содержание задания. Задание состоит из трех задач:

Задача 1. Построить фронтальную и профильную проекции геометрических тел с учетом их видимости в проекциях.

Задача 2. Достроить недостающие проекции линий (заданных преподавателем на одной из построенных трех проекций), принадлежащих поверхностям.

Задача 3. Построить наглядное изображение в прямоугольной изометрии группы геометрических тел в масштабе 1:2.

Методические указания. Задание выполнить карандашом на листе формата А3 (420х297). Данные для построения композиции геометрических тел взять из таблицы 5. В таблице 5 приняты следующие обозначения: Ц - цилиндр; К - конус; П - пирамида и С - сфера. Образец выполнения задания приведен на рисунке 3.

Построение комплексного чертежа группы геометрических тел следует начинать с горизонтальной проекции, так как основания цилиндра, конуса, пирамиды проецируются на горизонтальную плоскость проекций без искажения. Сначала изображается сетка по заданному размеру " а", на которой размещаются окружности диаметром равным диагонали клетки. Три построенные окружности являются горизонтальными проекциями цилиндра, конуса и сферы, а в четвертую – вписывается основание шестигранной пирамиды. Далее с помощью вертикальных линий связи строят фронтальные проекции по заданной высоте H геометрических тел. Профильную проекцию строят при помощи вертикальных и горизонтальных линий связи.

При определении видимости тел следует учитывать, что видимыми будут те тела, которые расположены ближе к наблюдателю или дальше от той плоскости проекций, на которой строится изображение.

После нанесения преподавателем на поверхностях проекций линий, студенты достраивают недостающие проекции этих линий самостоятельно (с учетом их видимости). Невидимые участки линий наносятся штриховой линией.

Для определения видимых и невидимых участков линий используют границу видимости, определяемую точками, лежащими на очерках поверхности.

 

Основные положения:

- точка лежит на поверхности, если она лежит на линии, принадлежащей этой поверхности;

- линия лежит на поверхности, если все ее точки принадлежат поверхности.

Наглядное (аксонометрическое) изображение группы геометрических тел строится в прямоугольной изометрии согласно ГОСТ 2.317-69.

Прямоугольная изометрия получается в случае, если все три оси декартовой системы координат, при проецировании на аксонометрическую плоскость проекций располагаются под равными углами к этой плоскости, а приведенные коэффициенты равны между собой (kx=ky=kz). Угол между аксонометрическими осями в прямоугольной изометрии составляет 1200.

Прямоугольная диметрия получается когда под равными углами равными 1200 к аксонометрической плоскости проекций находятся две координатные оси OX и OZ,а угол (b=620) наклона оси OY выбирается так, чтобы коэффициент искажения ky стал в два раза меньше чем kx и kz. Ось O¢Z¢располагают вертикально, тогда оси O¢X¢ и O¢Y¢ образуют с линией горизонта соответственно углы 70 10¢ и 410 25¢.

Аксонометрический чертеж обладает всеми свойствами параллельного проецирования. Аксонометрическая проекция квадрата – ромб, а окружности – эллипс. Построить аксонометрическое изображение объекта можно, либо построением каждой из характерных точек объекта по их координатным ломанным, либо с помощью вторичных проекций.

В прямоугольной изометрии изображают объекты криволинейной формы. В прямоугольной диметрии изображают объекты призматической и пирамидальной формы. В косоугольной фронтальной диметрии изображают детали, имеющие ряд окружностей, расположенных во взаимно параллельных плоскостях.

К преимуществам аксонометрического чертежа относятся: однопроекционность (наличие одной проекции), наглядность (возможность установить по чертежу форму объекта по его изображению), обратимость (возможность реконструкции объекта по его изображению), а к недостаткам – сложность построений изображений и измеримости объекта.

 

 

Таблица 5 - Исходные данные к задачам 1, 2, 3, в мм

Схема взаиморасположения геометрических тел № вар. a H Геометрические тела
       
      Ц К П С
      К П С Ц
      П С Ц К
      С Ц К П
      С П К Ц
      П К Ц С
      К Ц С П
      Ц С К П
      П К С Ц
      К П Ц С
      Ц К П С
      К П С Ц
      П С Ц К
      С Ц К П
      С П К Ц
      П К Ц С
      К Ц С П
      Ц С К П
      П К С Ц
      К П Ц С
      Ц К П С
      К П С Ц
      П С Ц К
      С Ц К П
      С П К Ц
      П К Ц С
      С П К Ц
      Ц С К П
      П К С Ц
      К П Ц С

 

 

Рисунок 3

 

2.3. Моделирование структуры геометрических объектов

Целевое назначение. Выполнение задания способствует:

- закреплению знаний студентов по решению задач в ортогональных проекциях на взаимное расположение в пространстве геометрических элементов;

- закреплению знаний студентов по способам преобразования комплексного чертежа (построению дополнительных проекций) в применении к решению метрических задач.

Содержание работы. Задание состоит из трех задач.

Задача 1. Построить проекции плоскости, проходящей через вершину В заданного треугольника АВС, перпендикулярной стороне АС. Построить проекции линии пересечения двух плоскостей с учетом их видимости.

Задача 2. Построить проекции плоскости, параллельной плоскости, заданной треугольником АВС, и отстоящей от неё на 30 мм.

Задача 3. Построить проекции сферы (с центром в точке D), касательной к плоскости, заданной треугольником АВС. Определить радиус сферы и построить проекции точки касания.

Методические указания. Задание выполнить карандашом на листе чертежной бумаги формата А3(420х297). Данные для задания взять из таблицы 6 по варианту. Задачи следует выполнить в масштабе 1:1. Образец выполнения задания приведен на рисунке 4.

Для решения первой задачи следует искомую плоскость, определить главными линиями (горизонталью и фронталью) перпендикулярными к стороне АС и проходящими через вершину В треугольника АВС. Для нахождения линии пересечения плоскостей следует горизонталь и фронталь плоскости ограничить произвольными точками Е и F. Точки соединить отрезком прямой линии и получить треугольник ВЕF. После этого построить линию пересечения двух треугольников АВС и ВЕF, у которых одна вершина В общая. Вторую общую точку К определить с помощью проецирующей плоскости-посредника, как точку пересечения стороны EF с треугольником ABC. Для определения видимости треугольников следует использовать конкурирующие точки, принадлежащие скрещивающимся прямым.

Вторая и третья задачи должны быть решены способом замены плоскостей проекций.

Для решения второй задачи следует:

- преобразовать комплексный чертеж так, чтобы заданная плоскость стала проецирующей плоскостью;

- из вершины A провести перпендикуляр к плоскости;

- отложить на нем заданное расстояние;

- через полученную точку провести искомую плоскость.

Для решения третьей задачи следует:

 

 

- преобразовать комплексный чертеж так, чтобы заданная плоскость стала проецирующей плоскостью;

- из центра сферы опустить перпендикуляр на заданную плоскость;

- из проекций центра сферы радиусом равным DK (см. рисунок 4) построить проекции сферы.

Таблица 6 - Исходные данные к задачам 1, 2, 3, в мм

№ вар. A   B C D
X   y z x y z x y z x y z
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         
                         

 

Рисунок 4

2.4. Моделирование метрических характеристик объектов

Целевое назначение. Закрепление знаний студентов по способам преобразования комплексного чертежа (построению дополнительных проекций) в применении к решению метрических задач.

Содержание работы. Задание состоит из четырех задач.

Задача 1. Определить истинную величину основания АВС трехгранной пирамиды DАВС.

Задача 2. Определить величину расстояния от вершины D до плоскости основания АВС трехгранной пирамиды DАВС.

Задача 3. Определить величину расстояния от вершины D до ребра ВС трехгранной пирамиды DАВС.

Задача 4. Определить истинную величину двугранного угла при ребре АВ трехгранной пирамиды DАВС.

Методические указания. Данные для комплексного чертежа взять из таблицы 6 по варианту. Задание выполнить на одном листе формата А3(420х297). Образец выполнения задания приведен на рисунке 5.

Задачи должны быть решены способом замены плоскостей проекц
Поделиться:





Воспользуйтесь поиском по сайту:



©2015 - 2024 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...