 |
Основные методы современной технологии проектирования алгоритмов
|
|
|
|
Понятие алгоритма. Свойства алгоритмов
Понятие алгоритма – одно из фундаментальных понятий информатики. Алгоритмизация наряду с моделированием выступает в качестве общего метода информатики. К реализации определенных алгоритмов сводятся процессы автоматизированной обработки информации различного рода, и именно это обстоятельство обусловило широкое использование этого понятия, интерес к нему в различных областях знания и деятельности, а также становление самой информатики.
Алгоритмы являются объектом систематического исследования пограничной между математикой и информатикой научной дисциплины, примыкающей к математической логике – теории алгоритмов.
Алгоритм – это описанная на некотором языке конечная система правил, определяющая содержание и порядок действий над некоторыми объектами, строгое выполнение которых дает решение поставленной задачи. (Алгоритм – это конечная последовательность действий, необходимых для решения некоторой задачи.) Разработка алгоритма решения задачи осуществляется путем ее разбиения на этапы (блоки), которые выполняются последовательно. При разработке алгоритма необходимо указать содержание всех этапов и порядок их выполнения.
Основные свойства алгоритмов:
1. дискретность – свойство, означающее, что каждый алгоритм состоит из отдельных законченных этапов (действий);
2. определенность (детерминированность) – свойство, указывающее на то, что каждый шаг в алгоритме должен быть строго определен и определен порядок выполнения отдельных шагов;
3. массовость – применимость алгоритма ко всем задачам рассматриваемого типа, при любых исходных данных.
4. результативность – свойство, состоящее в том, что любой алгоритм должен завершаться за конечное число шагов и при этом должен получиться определенный результат;
|
|
|
5. формальность – свойство, означающее, что исполнитель, выполняющий алгоритм, действует формально, т.е. отвлекается от содержания поставленной задачи и лишь строго выполняет инструкции;
6. конечность – свойство, означающее, что алгоритм должен содержать конечное число предписаний.
Для представления алгоритма используется несколько способов:
1. Словесный (описание на естественном языке)
2. Графический (на языке блок-схем)
3. С помощью символов специального языка программирования программ-псевдокодов
4. С использованием HIPO- диаграмм
5. С помощью схемы Насси-Шнейдермана
6. С помощью одного из известных алгоритмических языков программирования.
Алгоритмический язык – это специальный язык программирования, в котором алгоритм решения задачи (программа) записывается с помощью определенных правил построения конструкций для описания операций (синтаксиса языка). Предписание на выполнение определенной операции в АЯ называется оператором. (Алгоритмический язык – это система обозначений и правил для единообразной и точной записи алгоритмов и исполнения их.)
Разработка алгоритма называется алгоритмизацией задачи. В процессе алгоритмизации решение задачи разбивается на этапы, которые надо выполнить в определенной последовательности.
Блок-схема – это описание структуры алгоритма с помощью геометрических фигур с линиями-связями, показывающими порядок выполнения отдельных инструкций. Иначе: блок-схема – это графическое описание алгоритма.
Правила составления блок-схем:
1. Блок-схема строится сверху вниз.
2. В любой блок схеме имеется только один элемент, соответствующий началу алгоритма, и один элемент, соответствующий концу алгоритма.
3. Должен быть хотя бы один путь из начала блок-схемы к любому элементу.
|
|
|
4. Должен быть хотя бы один путь от каждого элемента блок-схемы в конец блок-схемы.
Основные методы современной технологии проектирования алгоритмов
1. Метод структурного проектирования. Любой алгоритм может быть построен из комбинаций трех базовых структур: линейный алгоритм (следование), разветвляющийся алгоритм (развилка) и циклический алгоритм (повтор).
2. Метод нисходящего проектирования. Первоначально выделяются главные функции, затем второстепенные.
3. Метод пошаговой детализации.
4. Метод модульности. Модуль — логически связанный фрагмент программы, выполняющий одну функцию и состоящий из обозримого числа шагов.
Прежде чем приступить к составлению блок-схемы, необходимо:
1. Регламентировать состав входа и выхода, т.е. определить имена входных данных, промежуточных и выходных результатов.
2. Дать наименование основной программе и вспомогательным алгоритмам.
Основы алгоритмизации и технологии программирования
Основные конструкции, использующиеся для построения блок-схем
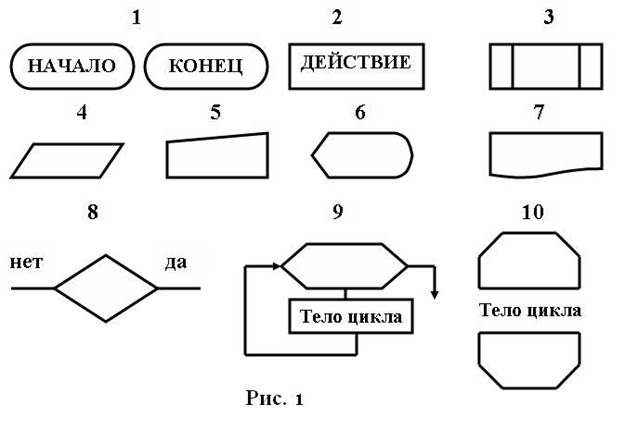 (1) Блок, характеризующий начало/конец алгоритма (для подпрограмм – вызов/возврат);
(2) Блок - процесс, предназначенный для описания отдельных действий;
(3) Блок - предопределенный процесс, предназначенный для обращения к вспомогательным алгоритмам (подпрограммам);
(4) Блок - ввода/вывода с неопределенного носителя;
(5) Блок - ввод с клавиатуры;
(6) Блок - вывод на монитор;
(7) Блок - вывод на печатающее устройство;
(8) Блок – решение (проверка условия или условный блок);
(9) Блок, описывающий блок с параметром;
(10) Блок – границы цикла, описывающий циклические процессы типа: «цикл с предусловием», «цикл с постусловием»;
Описания алгоритма в словесной форме, на псевдокоде или в виде блок-схемы допускают некоторый произвол при изображении команд. Вместе с тем она настолько достаточна, что позволяет человеку понять суть дела и исполнить алгоритм. На практике исполнителями алгоритмов выступают компьютеры. Поэтому алгоритм, предназначенный для исполнения на компьютере, должен быть записан на «понятном» ему языке, такой формализованный язык называют языком программирования.
Программа – описание структуры алгоритма на языке алгоритмического программирования. Программа на языке декларативного программирования представляет собой совокупность описанных знаний и не содержит явного алгоритма исполнения.
Основные алгоритмические конструкции
Элементарные шаги алгоритма можно объединить в следующие алгоритмические конструкции: линейные (последовательные), разветвляющиеся, циклические и рекурсивные.
Линейная алгоритмическая конструкция
Линейной называют алгоритмическую конструкцию, реализованную в виде последовательности действий (шагов), в которой каждое действие (шаг) алгоритма выполняется ровно один раз, причем после каждого i- гo действия (шага) выполняется (i+ 1)-е действие (шаг), если i -e действие – не конец алгоритма.
Пример 1. Опишем алгоритм сложения двух чисел на псевдокоде в виде блок-схемы (рис. 2).
(1) Блок, характеризующий начало/конец алгоритма (для подпрограмм – вызов/возврат);
(2) Блок - процесс, предназначенный для описания отдельных действий;
(3) Блок - предопределенный процесс, предназначенный для обращения к вспомогательным алгоритмам (подпрограммам);
(4) Блок - ввода/вывода с неопределенного носителя;
(5) Блок - ввод с клавиатуры;
(6) Блок - вывод на монитор;
(7) Блок - вывод на печатающее устройство;
(8) Блок – решение (проверка условия или условный блок);
(9) Блок, описывающий блок с параметром;
(10) Блок – границы цикла, описывающий циклические процессы типа: «цикл с предусловием», «цикл с постусловием»;
Описания алгоритма в словесной форме, на псевдокоде или в виде блок-схемы допускают некоторый произвол при изображении команд. Вместе с тем она настолько достаточна, что позволяет человеку понять суть дела и исполнить алгоритм. На практике исполнителями алгоритмов выступают компьютеры. Поэтому алгоритм, предназначенный для исполнения на компьютере, должен быть записан на «понятном» ему языке, такой формализованный язык называют языком программирования.
Программа – описание структуры алгоритма на языке алгоритмического программирования. Программа на языке декларативного программирования представляет собой совокупность описанных знаний и не содержит явного алгоритма исполнения.
Основные алгоритмические конструкции
Элементарные шаги алгоритма можно объединить в следующие алгоритмические конструкции: линейные (последовательные), разветвляющиеся, циклические и рекурсивные.
Линейная алгоритмическая конструкция
Линейной называют алгоритмическую конструкцию, реализованную в виде последовательности действий (шагов), в которой каждое действие (шаг) алгоритма выполняется ровно один раз, причем после каждого i- гo действия (шага) выполняется (i+ 1)-е действие (шаг), если i -e действие – не конец алгоритма.
Пример 1. Опишем алгоритм сложения двух чисел на псевдокоде в виде блок-схемы (рис. 2).
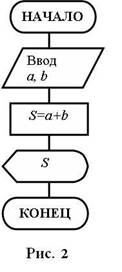 Псевдокод:
Ввод двух чисел а, b.
Вычисляем сумму S = а + b.
Вывод S.
Конец.
Разветвляющаяся алгоритмическая конструкция
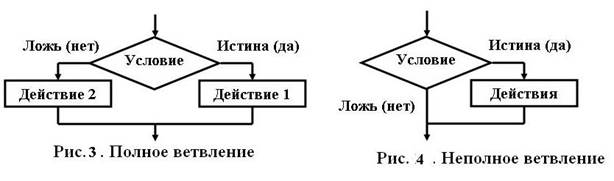
Разветвляющейся (или ветвящейся) называется алгоритмическая конструкция, обеспечивающая выбор между двумя альтернативами в зависимости от значения входных данных. При каждом конкретном наборе входных данных разветвляющийся алгоритм сводится к линейному. Различают неполное (если – то) и полное (если – то – иначе) ветвления. Полное ветвление позволяет организовать две ветви в алгоритме (то или иначе), каждая из которых ведет к общей точке их слияния, так что выполнение алгоритма продолжается независимо от того, какой путь был выбран (рис. 3). Неполное ветвление предполагает наличие некоторых действий алгоритма только на одной ветви (то), вторая ветвь отсутствует, т.е. для одного из результатов проверки никаких действий выполнять не надо, управление сразу переходит к точке слияния (рис. 4).
Псевдокод:
Ввод двух чисел а, b.
Вычисляем сумму S = а + b.
Вывод S.
Конец.
Разветвляющаяся алгоритмическая конструкция
Разветвляющейся (или ветвящейся) называется алгоритмическая конструкция, обеспечивающая выбор между двумя альтернативами в зависимости от значения входных данных. При каждом конкретном наборе входных данных разветвляющийся алгоритм сводится к линейному. Различают неполное (если – то) и полное (если – то – иначе) ветвления. Полное ветвление позволяет организовать две ветви в алгоритме (то или иначе), каждая из которых ведет к общей точке их слияния, так что выполнение алгоритма продолжается независимо от того, какой путь был выбран (рис. 3). Неполное ветвление предполагает наличие некоторых действий алгоритма только на одной ветви (то), вторая ветвь отсутствует, т.е. для одного из результатов проверки никаких действий выполнять не надо, управление сразу переходит к точке слияния (рис. 4).
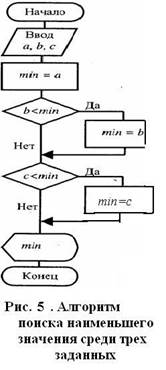
 Рассмотрим стандартный алгоритм поиска наибольшего (наименьшего) значения среди нескольких заданных. Основная идея алгоритма сводится к следующему: за наибольшее (наименьшее) принимаем значение любого из данных. Поочередно сравниваем оставшиеся данные с наибольшим (наименьшим). если окажется, что очередное значение входного данного больше (меньше) наибольшего (наименьшего), то наибольшему (наименьшему) присваиваем это значение. Таким образом, сравнив все входные данные, найдем наибольшее (наименьшее) среди них. Алгоритм использует неполное ветвление.
Пример 2.
Заданы три числа. Найти значение наименьшего из них Заданные числа обозначим: а, b, с; результирующее наименьшее – min. На рис. 5 представлена блок-схема алгоритма решения данной задачи.
Рассмотрим стандартный алгоритм поиска наибольшего (наименьшего) значения среди нескольких заданных. Основная идея алгоритма сводится к следующему: за наибольшее (наименьшее) принимаем значение любого из данных. Поочередно сравниваем оставшиеся данные с наибольшим (наименьшим). если окажется, что очередное значение входного данного больше (меньше) наибольшего (наименьшего), то наибольшему (наименьшему) присваиваем это значение. Таким образом, сравнив все входные данные, найдем наибольшее (наименьшее) среди них. Алгоритм использует неполное ветвление.
Пример 2.
Заданы три числа. Найти значение наименьшего из них Заданные числа обозначим: а, b, с; результирующее наименьшее – min. На рис. 5 представлена блок-схема алгоритма решения данной задачи.
 Алгоритмическая конструкция «Цикл»
Циклической (или циклом) называют алгоритмическую конструкцию, в кoтoрoй некая, идущая подряд группа действий (шагов) алгоритма может выполняться несколько раз, в зависимости от входных данных или условия задачи. Группа повторяющихся действий на каждом шагу цикла называется телом цикла. Любая циклическая конструкция содержит себе элементы ветвящейся алгоритмической конструкции.
Рассмотрим три типа циклических алгоритмов: ц uкл с параметром (который называют арифметическим циклом), цикл с предусловием и цикл с постусловием (их называют итерационными).
Арифметический цикл
В арифметическом цикле число его шагов (повторений) однозначно определяется правилом изменения параметра, которое задается с помощью начального (N) и конечного (К) значений параметра и шагом (h) его изменения. Т.е., на первом шаге цикла значение параметра равно N, на втором – N + h, на третьем – N + 2h и т.д. На последнем шаге цикла значение параметра не больше К, но такое, что дальнейшее его изменение приведет к значению, большему, чем К.
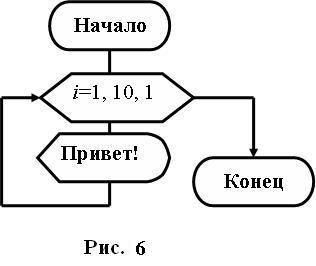
Пример 3.
Вывести 10 раз слово «Привет!».
Параметр цикла обозначим i, он будет отвечать за количество выведенных слов. При i =1 будет выведено первое слово, при i =2 будет выведено второе слова и т. д. Так как требуется вывести 10 слов, то последнее значение параметра i =10. В заданном примере требуется 10 раз повторить одно и то же действие: вывести слово «Привет!». Составим алгоритм, используя арифметический цикл, в котором правило изменения параметра i=1,10, 1. т. е. начальное значение параметра i=1; конечное значение i=10; шаг изменения h=1. На рис. 6 представлена блок-схема алгоритма решения данной задачи.
Алгоритмическая конструкция «Цикл»
Циклической (или циклом) называют алгоритмическую конструкцию, в кoтoрoй некая, идущая подряд группа действий (шагов) алгоритма может выполняться несколько раз, в зависимости от входных данных или условия задачи. Группа повторяющихся действий на каждом шагу цикла называется телом цикла. Любая циклическая конструкция содержит себе элементы ветвящейся алгоритмической конструкции.
Рассмотрим три типа циклических алгоритмов: ц uкл с параметром (который называют арифметическим циклом), цикл с предусловием и цикл с постусловием (их называют итерационными).
Арифметический цикл
В арифметическом цикле число его шагов (повторений) однозначно определяется правилом изменения параметра, которое задается с помощью начального (N) и конечного (К) значений параметра и шагом (h) его изменения. Т.е., на первом шаге цикла значение параметра равно N, на втором – N + h, на третьем – N + 2h и т.д. На последнем шаге цикла значение параметра не больше К, но такое, что дальнейшее его изменение приведет к значению, большему, чем К.
Пример 3.
Вывести 10 раз слово «Привет!».
Параметр цикла обозначим i, он будет отвечать за количество выведенных слов. При i =1 будет выведено первое слово, при i =2 будет выведено второе слова и т. д. Так как требуется вывести 10 слов, то последнее значение параметра i =10. В заданном примере требуется 10 раз повторить одно и то же действие: вывести слово «Привет!». Составим алгоритм, используя арифметический цикл, в котором правило изменения параметра i=1,10, 1. т. е. начальное значение параметра i=1; конечное значение i=10; шаг изменения h=1. На рис. 6 представлена блок-схема алгоритма решения данной задачи.
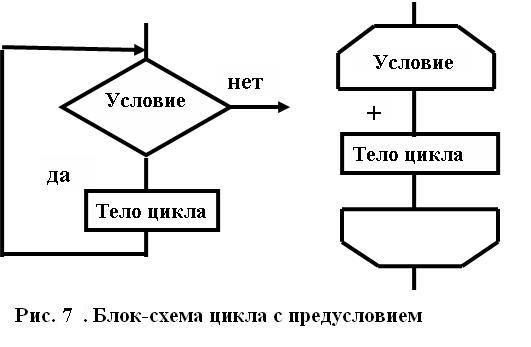
 Цикл с предусловием
Количество шагов цикла заранее не определено и зависит от входных данных задачи. В данной циклической структуре сначала проверяется значение условного выражения (условие) перед выполнением очередного шага цикла. Если значение условного выражения истинно, исполняется тело цикла. После чего управление вновь передается проверке условия и т.д. Эти действия повторяются до тех пор, пока условное выражение не примет значение ложь. При первом же несоблюдении условия цикл завершается.
Блок-схема данной конструкции представлена на рис. 7 двумя способами: с помощью условного блока а и с помощью блока границы цикла б. Особенностью цикла с предусловием является то, что если изначально условное выражение ложно, то тело цикла не выполнится ни разу.
Цикл с предусловием
Количество шагов цикла заранее не определено и зависит от входных данных задачи. В данной циклической структуре сначала проверяется значение условного выражения (условие) перед выполнением очередного шага цикла. Если значение условного выражения истинно, исполняется тело цикла. После чего управление вновь передается проверке условия и т.д. Эти действия повторяются до тех пор, пока условное выражение не примет значение ложь. При первом же несоблюдении условия цикл завершается.
Блок-схема данной конструкции представлена на рис. 7 двумя способами: с помощью условного блока а и с помощью блока границы цикла б. Особенностью цикла с предусловием является то, что если изначально условное выражение ложно, то тело цикла не выполнится ни разу.
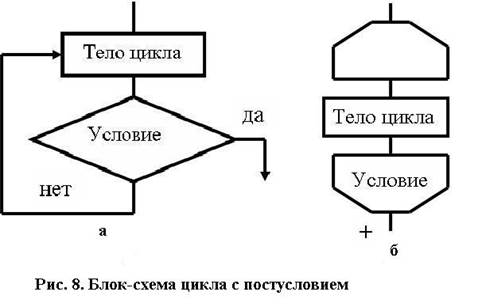
 Цикл с постусловием
Как и в цикле с предусловием, в циклической конструкции с постусловием заранее не определено число повторений тела цикла, оно зависит от входных данных задачи. В отличие от цикла с предусловием, тело цикла с постусловием всегда будет выполнено хотя бы один раз, после чего проверяется условие. В этой конструкции тело цикла будет выполняться до тех пор, пока значение условного выражения ложно. Как только оно становится истинным, выполнение команды прекращается. Блок-схема данной конструкции представлена на рис. 8 двумя способами: с помощью условного блока а и с помощью блока управления б.
Цикл с постусловием
Как и в цикле с предусловием, в циклической конструкции с постусловием заранее не определено число повторений тела цикла, оно зависит от входных данных задачи. В отличие от цикла с предусловием, тело цикла с постусловием всегда будет выполнено хотя бы один раз, после чего проверяется условие. В этой конструкции тело цикла будет выполняться до тех пор, пока значение условного выражения ложно. Как только оно становится истинным, выполнение команды прекращается. Блок-схема данной конструкции представлена на рис. 8 двумя способами: с помощью условного блока а и с помощью блока управления б.
 Рекурсивный алгоритм
Рекурсивным называется алгоритм, организованный таким образом, что в процессе выполнения команд на каком-либо шаге он прямо или косвенно обращается сам к себе.
Простые типы данных: переменные и константы
Реальные данные, которые обрабатывает программа, - это целые и вещественные числа, символы и логические величины. Эти простые типы данных называют базовыми. Все данные, обрабатываемые компьютером, хранятся в ячейках памяти компьютера, каждая из которых имеет свой адрес. Для того чтобы не следить за тем, по какому адресу будут записаны те или иные данные, в языках программирования используется понятие переменной, позволяющее отвлечься от адреса ячейки памяти и обращаться к ней с помощью имени (идентификатора).
Переменная – есть именованный объект (ячейка памяти), который может изменять свое значение. Имя переменной указывает на значение, а способ ее хранения и адрес остаются скрытыми от программиста. Кроме имени и значения, переменная имеет тип, определяющий, какая информация находится в памяти. Тип переменной задает:
Рекурсивный алгоритм
Рекурсивным называется алгоритм, организованный таким образом, что в процессе выполнения команд на каком-либо шаге он прямо или косвенно обращается сам к себе.
Простые типы данных: переменные и константы
Реальные данные, которые обрабатывает программа, - это целые и вещественные числа, символы и логические величины. Эти простые типы данных называют базовыми. Все данные, обрабатываемые компьютером, хранятся в ячейках памяти компьютера, каждая из которых имеет свой адрес. Для того чтобы не следить за тем, по какому адресу будут записаны те или иные данные, в языках программирования используется понятие переменной, позволяющее отвлечься от адреса ячейки памяти и обращаться к ней с помощью имени (идентификатора).
Переменная – есть именованный объект (ячейка памяти), который может изменять свое значение. Имя переменной указывает на значение, а способ ее хранения и адрес остаются скрытыми от программиста. Кроме имени и значения, переменная имеет тип, определяющий, какая информация находится в памяти. Тип переменной задает:
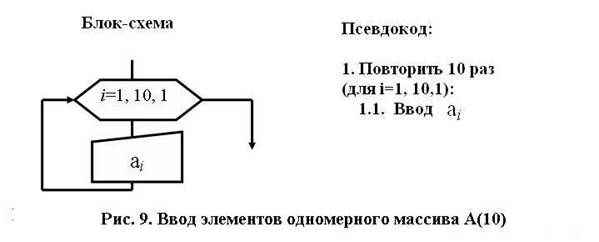 Пример 4.
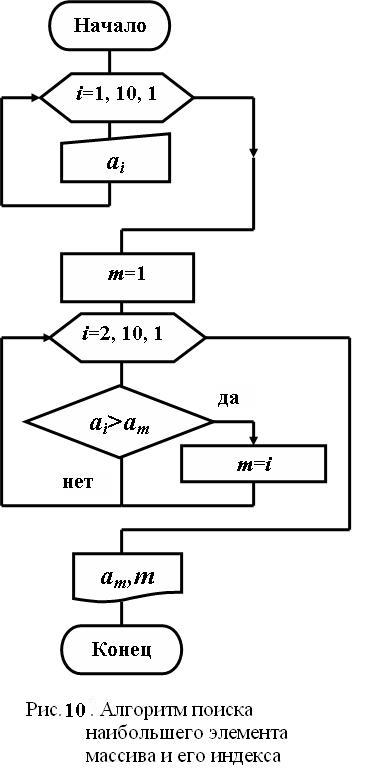
В заданном числовом массиве A(10) найти наибольший элемент и его индекс, при условии, что такой элемент в массиве существует, и единственный.
Обозначим индекс наибольшего элемента т. Будем считать, что первый элемент массива является наибольшим (т = 1). Сравним поочередно наибольший с остальными элементами массива. Если оказывается, что текущий элемент массива а i (тот, c которым идет сравнение) больше выбранного нами наибольшего ат, то считаем его наибольшим (т = i) (рис.10).
Пример 4.
В заданном числовом массиве A(10) найти наибольший элемент и его индекс, при условии, что такой элемент в массиве существует, и единственный.
Обозначим индекс наибольшего элемента т. Будем считать, что первый элемент массива является наибольшим (т = 1). Сравним поочередно наибольший с остальными элементами массива. Если оказывается, что текущий элемент массива а i (тот, c которым идет сравнение) больше выбранного нами наибольшего ат, то считаем его наибольшим (т = i) (рис.10).
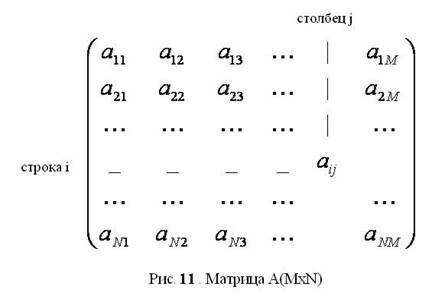
 Рассмотрим двумерный массив (шкаф с множеством ящиков, положение которых определяется двумя координатами – по горизонтали и по вертикали). В математике двумерный массив (таблица чисел) называется матрицей. Каждый ее элемент имеет два индекса а ij , первый индекс i определяет номер строки, в которой находится элемент (координата по горизонтали), а второй j – номер столбца (координата по вертикали). Двумерный массив характеризуется двумя размерностями N и М, определяющими число строк и столбцов соответственно (рис. 11).
Рассмотрим двумерный массив (шкаф с множеством ящиков, положение которых определяется двумя координатами – по горизонтали и по вертикали). В математике двумерный массив (таблица чисел) называется матрицей. Каждый ее элемент имеет два индекса а ij , первый индекс i определяет номер строки, в которой находится элемент (координата по горизонтали), а второй j – номер столбца (координата по вертикали). Двумерный массив характеризуется двумя размерностями N и М, определяющими число строк и столбцов соответственно (рис. 11).
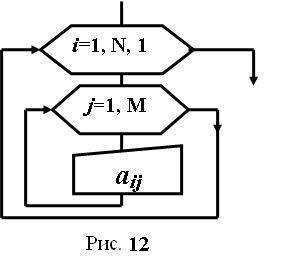
 Ввод элементов двумерного массива осуществляется построчно, в свою очередь, ввод каждой строки производится поэлементно, тем самым определяется циклическая конструкция, реализующая вложение циклов. Внешний цикл определяет номер вводимой строки (i), внутренний – номер элемента по столбцу (j). На рис. 12 представлен алгоритм ввода матрицы A(MxN).
Ввод элементов двумерного массива осуществляется построчно, в свою очередь, ввод каждой строки производится поэлементно, тем самым определяется циклическая конструкция, реализующая вложение циклов. Внешний цикл определяет номер вводимой строки (i), внутренний – номер элемента по столбцу (j). На рис. 12 представлен алгоритм ввода матрицы A(MxN).
 Пример 5.
Задана матрица символов (100х100), представляющая собой карту ночного неба; звездам на карте соответствует символы «*». Определить: сколько звезд на карте?
Алгоритм решения задачи достаточно прост, необходимо перебрать все элементы матрицы и посчитать, сколько среди них символов «*». Обозначим К переменную – счетчик. На рис 13. представлена блок-схема решения этой задачи.
Пример 5.
Задана матрица символов (100х100), представляющая собой карту ночного неба; звездам на карте соответствует символы «*». Определить: сколько звезд на карте?
Алгоритм решения задачи достаточно прост, необходимо перебрать все элементы матрицы и посчитать, сколько среди них символов «*». Обозначим К переменную – счетчик. На рис 13. представлена блок-схема решения этой задачи.

|
|
|
|
|
|
|
|
|
|
|
|
|


