Задание 1. Калибровка крутильного маятника.

Краткая теория

Моментом инерции I называется физическая величина, характеризующая способность данного тела запасать количество вращательного движения (то есть момента импульса L).
Определяющей формулой для I является:

 

, (1.1)

 

где L – момент импульса, I – момент инерции тела, w – угловая скорость.

Можно показать, что момент инерции тела относительно некоторой оси вращения зависит от распределения массы данного тела вокруг выбранной оси и может быть рассчитан по формуле:

 

, (1.2)

 

где m_i – масса точки тела, r_i – расстояние этой точки до оси вращения.

Момент импульса относительно любой оси можно рассчитать, пользуясь теоремой Штейнера: момент инерции I_а тела относительно произвольной оси а равен сумме момента инерции I_c тела относительно параллельной ей оси, проходящей через центр масс С тела и произведения массы тела m на квадрат расстояния d между этими осями:

 

. (1.3)

 

Рис.1.1. К теореме Штейнера

Докажем эту теорему. На рис.1.1. оси а и ас направлены перпендикулярно плоскости чертежа, а расстояние от малого элемента тела массой dm до этих осей обозначены соответственно r и rc. По теореме косинусов, . и ,

 

где x^*= r_c cosj - абсцисса элемента dm тела в системе координат с началом в центре масс тела и осью абсцисс, пересекающей оси а и а_с и лежащей в перпендикулярной им плоскости. Из определения центра масс следует, что

 

,

 

так как центр масс тела совпадает с началом координат. Таким образом справедливость соотношения (1.3) доказана.

Рассмотрим несколько примеров расчета момента инерции для тел простейшей формы.

Пример 1. Момент инерции сплошного однородного кругового цилиндра массой m и радиусом R относительно его оси.

Разобьем мысленно цилиндр на очень большое число соосных тонкостенных цилиндров. Пусть r – радиус какого-либо из них, а толщина его стенки dr << r (рис.1.2.). Тогда момент инерции этого элемента сплошного цилиндра равен

,

 

 

m         H         Рис.1.2. Сплошной цилиндр

так как все малые элементы его находятся на одном и том же расстоянии R от его оси. . (*) где Н – высота цилиндра; r - его плотность. Искомый момент инерции сплошного цилиндра находим, суммируя момен- ты инерции всех его малых элементов, т.е. интегрируя выражение (*) по r от 0 до R:

 

 

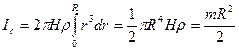, (1.4)

 

так как масса цилиндра .

Пример 2. Момент инерции однородного тонкого стержня массой m и длиной l относительно оси, проходящей через его середину.

Разобьем мысленно стержень на малые отрезки. Пусть x – расстояние от одного из таких элементов до оси, а dx – его длина. Тогда момент инерции этого элемента

 

, (**)

 

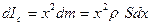где S – площадь поперечного сечения стержня (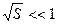); r - его плотность. Момент инерции одной половины стержня находим интегрируя выражение (**) от 0 до , а искомый момент всего стержня вдвое больше:

 

, (1.5)

 

так как масса стержня m = r l S.

Однако, если тело имеет сложную, то расчёт его момента инерции по формуле (1.2) становится трудным и в ряде случаев его проще определить опытным способом.

Одним из методов опытного экспериментального определения момента инерции тела является метод крутильных колебаний.

Схема крутильного маятника изображена на рис. 1.3.

Он представляет собой упругую проволоку с закреплённым верхним концом, к нижнему концу которой жёстко присоединено изучаемое тело. Поворачивая тело на угол j, мы создаём в проволоке вращающий момент упругой силы М_упр, который по закону Гука пропорционален деформации кручения j:

 

. (1.6)

 

Коэффициент пропорциональности в законе Гука называется модулем кручения и зависит от параметров проволоки:

 

, (1.7)

 

где d – диаметр проволоки, l – длина проволоки, N – модуль сдвига материала проволоки.

По второму закону Ньютона, момент упругой силы создаёт угловое ускорение, пропорциональное этому моменту:

 

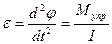. (1.8)

 

Таким образом, свободное вращение крутильного маятника при пренебрежении силами трения, будет описываться дифференциальными уравнениями, объединяющими второй закон Ньютона и Гука:

. (1.9)

 

Интегрируя это выражение получим его решение

 

. (1.10)

 

Следовательно, при допустимости сделанных нами упрощений, маятник будет совершать гармонические колебания с периодом

 

. (1.11)

 

Как видно из формулы (1.11), используя колебания крутильного маятника, зная любые две величины из (T, f, I) рассчитать оставшуюся.

 

Задание 1. Калибровка крутильного маятника.

Поделиться:

Воспользуйтесь поиском по сайту: