 |
Арифметические операции и выражения
|
|
|
|
Знаки операций предназначены для обозначения тех или иных арифметических, логических или других действий. Они бывают двух типов: состоящие из небуквенных символов (например, +, -, * и т.д.) и буквенные операции (например, not, mod, div и т. д.), представляющие собой зарезервированные слова. Операции над данными делятся на унарные (применимые к одному операнду) и бинарные (применимые к двум операндам). Приведем примеры бинарных арифметических операций (в таблице буква I обозначает целые типы, R — вещественные типы):
| Знак | Выражение | Типы операндов | Тип результата | Операция |
| + | А+В | R,R I,I I,R; R,I | R I R | Сложение |
| - | А-В | R,R I,I I,R; R,I | R I R | Вычитание |
| * | А*В | R,R I,I I,R; R,I | R I R | Умножение |
| / | А/В | R,R I,I I,R; R,I | R R R | Вещественное деление |
| Div | A div B | I, I | I | Целое деление |
| Mod | A mod B | I, I | I | Остаток от деления |
Арифметическое выражение задает порядок выполнения действий над числовыми величинами. Арифметические выражения содержат арифметические операции, функции, операнды, круглые скобки. Одна константа или одна переменная — простейшая форма арифметического выражения.
Порядок выполнения операций в арифметическом выражении подчиняется трем правилам:
1. Правилу скобок. Оно гласит, что первыми выполняются операции в скобках. Если имеется несколько пар вложенных скобок, вычисления начинаются с самых внутренних скобок.
2. Правилу учета приоритета операций: вначале вычисляются значения функций, затем выполняются операции умножения и деления и в последнюю очередь - операции сложения и вычитания.
3. Правилу следования: операции одинакового старшинства (приоритета) выполняются слева направо в порядке их следования.
Пример. Цифрами сверху указан порядок выполнения операций:
|
|
|

Выражение имеет целый тип, если в результате его вычисления получается величина целого типа. Выражение имеет вещественный тип, если результатом его вычисления является вещественная величина.
Стандартные функции
В качестве операндов в выражении, кроме констант и переменных, можно использовать стандартные функции. Аргументы функций обязательно заключаются в круглые скобки. Приоритет выполнения функции выше, чем приоритет выполнения арифметических операций. Рассмотрим стандартные функции Турбо Паскаля (в таблице буква I обозначает целые типы, R — вещественные типы):
| Обращение | Тип аргумента | Тип результата | Тип действия |
| pi | - | R | Число π |
| abs(x) | I, R | I, R | Модуль (абсолютная величина) числа х |
| sqr(x) | I, R | I, R | Квадрат х |
| sqrt(x) | I, R | R | Корень квадратный из х (х≥0) |
| sin(x) | I, R | R | Синус х (х в радианах) |
| cos(x) | I, R | R | Косинус х (х в радианах) |
| arctan(x) | I, R | R | Арктангенс х (результат в радианах) |
| exp(x) | I, R | R | Экспонента е в степени х (е≈2,71828) |
| ln(x) | I, R | R | Натуральный логарифм х (x>0) |
| trunc(x) | R | I | Целая часть х |
| int(x) | I, R | R | Целая часть х |
| round(x) | R | I | Округление х до ближайшего целого |
| frac(x) | I, R | R | Дробная часть х |
| random | - | I | Случайное число [0,1) |
| random(x) | I | R | Случайное число [0,х) |
| dec(x,[n]) | I | I | Уменьшение х на n, при отсутствии n – на 1 |
| inc(x,[n]) | I | I | Увеличение х на n, при отсутствии n – на 1 |
| odd(x) | Longint | Boolean | true, если значение x нечетное; false, если x четное |
| ord(x) | любой порядковый | Longint | Порядковый номер значения х в его типе. Если х – символ, то функция возвращает код символа |
| pred(x) | любой порядковый | тот же, что для x | Предыдущее относительно х значение в его типе |
| succ(x) | любой порядковый | тот же, что для x | Следующее относительно х значение в его типе |
| chr(x) | Byte | Char | Определяет символ с указанным кодом (х – число, определяющее код символа) |
Турбо Паскале не содержит некоторые часто используемые математические функции, поэтому при их вычислении используют эквивалентные математические формулы:
|
|
|
| Функция | Эквивалентная математическая формула | Запись в программе |
| ax | 
| exp(x*ln(a)) |
| tg(x) | 
| sin(x)/cos(x) |
| arcsin(x) | 
| arctan(x/sqrt(1-x*x)) |
| arccos(x) | 
| arctan(sqrt(1-x*x)/x) |
| logax | 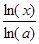
| ln(x)/ln(a) |
При возведении в небольшую целую степень вместо операции возведения в степень рекомендуется использовать операцию умножения, поскольку возведение в степень выполняется на несколько порядков дольше умножения и не позволяет обрабатывать отрицательные аргументы.
Оператор присваивания
Значение переменной может быть задано или изменено с помощью оператора присваивания, который имеет вид:
<имя>:=<выражение>;
где <имя> - это имя переменной или функции;
:= - знак операции присваивания.
Оператор присваивания позволяет заменить текущее значение переменной, стоящей слева от знака присваивания, новым значением, задаваемым выражением, стоящим справа.
С правой стороны располагается выражение, которое после вычисления дает некоторое значение. С левой стороны указывается имя переменной, которой это значение присваивается. Данное обстоятельство позволяет использовать с левой и правой стороны знака присваивания имя одной и той же переменной. Пусть, например, имеются следующие операторы:
Var
х, а: real;
.....
х:=2.5;
а:=1.25;
х:=х+а;
После выполнения этих операторов переменная х будет иметь значение 3.75, так как первоначально произойдет вычисление выражения х + а в виде сложения двух констант: 2.5+ 1.25 = 3.75, а затем это значение присваивается переменной х (предыдущее значение х, равное 2.5, заменится новым - 3.75).
Следует обратить внимание на следующее правило: типы переменной и выражения должны быть одинаковыми. Исключение составляет случай, когда выражение имеет целый тип, а переменная — вещественный.
|
|
|
12 |


