 |
5. Понятие системы счисления. 6. Алгоритм перевода из системы с произвольным основанием в десятичную. 7. Алгоритм перевода из десятичной системы в систему с произвольным основанием.
|
|
|
|
5. Понятие системы счисления.
Система счисления – способ записи и наименования чисел с помощью ограниченного числа символов.
1. Непозиционная. Каждая цифра сохраняет свое значение независимо от ее места в записи числа.
2. Позиционная. Значение цифры зависит не только от ее вида, но и от ее места нахождения (позиции разряда в записи числа)
С ростом основания существенно повышаются требования к аппаратуре, выполняющей формирование и распознавание элементарных сигналов, соответствующих различным символам.
В теории информации вычислено, что наиболее удобным основанием является число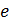 
. Очевидно, что такого основания быть не может. Ближайшее целое – 3. Однако используется двоичная система счисления, так как она надёжнее.
При анализе работы вычислительных средства, при оформлении документации используется шестнадцатеричная система.
6. Алгоритм перевода из системы с произвольным основанием в десятичную.
Раскладываем по разрядам.
7. Алгоритм перевода из десятичной системы в систему с произвольным основанием.
Делим на основание системы счисления.
8. Использование 2, 8, 16 систем счисления. Способы перевода.
Двоичная система счисления используется в ЭВМ. Восьмеричная и шестнадцатеричная – для составления документации, анализа работы ЭВМ.
Методы перевода:
1. Метод непосредственной замены. Сводится к реализации соотношения 
2. Табличный метод. Составляется таблица, в нижней строке которой фиксируется результат перевода, процедура которого напоминает процедуру взвешивания.
3. Частный случай перевода. Для перевода любого числа x из системы счисления с основанием 
в систему счисления с основанием 
, необходимо заменить каждую цифру в коде 
её r-разрядным 
кодом
|
|
|
4. Метод деления. Делим на основание системы счисления в исходной системе счисления.
9. Способы представления целых чисел в ЭВМ.
1. Прямой код. Двоичное представление числа, в котором положительное число записывается в его естественной форме, а отрицательное – в старшем бите 1.
2. Обратный код. Обратный код положительного числа совпадает с его записью в прямом коде. При записи отрицательного числа все его цифры, кроме знакового разряда, инвертируются.
3. Дополнительный код. Запись положительного числа такая же. Запись отрицательного числа получается добавлением единицы к обратному коду. Дополнительный код позволяется осуществлять операции сложения чисел с разными знаками.
10. Способы представления вещественных чисел в ЭВМ
Для представления вещественных чисел используются форматы с плавающей точкой. Число заносится в память компьютера в экспоненциальной форме, то есть в виде двух сомножителей: значащей части (мантисса) и основания системы счисления в соответствующей степени (порядок).
11. Способы представления текстовой информации в ЭВМ.
При кодировке текста в память последовательно заносятся коды символов, составляющих текст, и команд, управляющих внешним видом и размещением символов.
При разработке всех кодовых таблиц используется соглашение: первая половина таблица – интернациональная, то есть одинаковая во всех кодировках: 0-32 – коды операций с текстом, 33-127 – знаки препинания, арифметических действий, цифры, буквы латинского алфавита; вторая половина отводится под национальные и специальные знаки.
|
|
|
