 |
Порядок проведения измерений
|
|
|
|
Лабораторная работа №1
«Методы, схемы и средства измерений отклонений формы типовых поверхностей деталей машин»
Цель работы: Изучить некоторые методы, схемы и средства измерений следующих отклонений формы:
- отклонение от цилиндричности (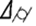 ),
),
- отклонение от круглости (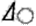 ),
),
- отклонение профиля продольного сечения (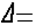 ),
),
- отклонение от прямолинейности (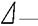 ),
),
- отклонение от плоскостности ( ).
).
Общая теоретическая часть
Отклонением формы в соответствии с ГОСТ 24642-81называется отклонение формы реальной поверхности (ограничивающей тело и отделяющей его от окружающей среды) от формы номинальной поверхности. Под номинальной понимается идеальная поверхность, форма которой задана чертежом или другой технической документацией. Отклонения формы могут рассматриваться и применительно к профилю – линии пересечения поверхности с плоскостью, обычно, перпендикулярной к поверхности.
Неровности, относящиеся к шероховатости поверхности, в отклонениях формы поверхности не включаются. При измерении отклонений формы исключение влияния шероховатости происходит за счет применения достаточно большого радиуса измерительного наконечника или электрических фильтров, не пропускающих высокочастотную составляющую измерительного сигнала. Волнистость поверхности относится к отклонениям формы. В обоснованных случаях, которые предусмотрены техническими условиями, устанавливают самостоятельные нормы на волнистость поверхности.
Отклонение формы оценивается по всей поверхности (по всему профилю) или на нормируемом участке, если заданы его площадь, длина или угол сектора, а в необходимых случаях и расположение его на поверхности. Если расположение нормируемого участка не задано, то его считают любым в пределах всей поверхности или профиля.
|
|
|
 Рис. 1.
Рис. 1.
Отсчет отклонений формы поверхности производится от прилегающей поверхности, имеющей номинальную форму, соприкасающейся с реальной и расположенной вне материала детали так, чтобы отклонение от нее наиболее удаленной точки реальной поверхности в пределах нормируемого участка имело минимальное значение. Отклонение формы профиля оценивается аналогично – от прилегающего профиля.
Следует заметить, что условие минимального значения отклонения в наиболее удаленной точке не распространяется на прилегающий цилиндр и прилегающую окружность, так как их определения связаны с понятием о предельных поверхностях, ограничивающих поле допуска размера.
Определения отклонений и допусков формы, а так же прилегающих профилей и поверхностей для каждого отклонения см. в Приложении 1 к лабораторному практикуму и в примечаниях к нему.
Параметром для количественной оценки отклонения формы является наибольшее расстояние Δ от точек реальной поверхности (профиля) до прилегающей поверхности (профиля) по нормали к последней (Рис.1.а) в пределах нормируемого участка L. При измерении отклонений формы допускается их оценка относительно средней поверхности или среднего профиля. Средняя поверхность имеет форму номинальной поверхности и расположена так, чтобы среднее квадратическое отклонение точек реальной поверхности от средней в пределах нормируемого участка имело минимальное значение. Аналогично определяется и средний профиль. Отклонение формы при отсчете от средней поверхности (профиля) равно сумме (Δ) абсолютных величин наибольших отклонений точек реальной поверхности по обе стороны от средней (Рис.1.б). Чаще всего такой подход используется при измерениях на координатно-измерительных машинах (КИМ) и при лазерном сканировании поверхности, т.к. математически и алгоритмически проще рассчитать именно средний профиль (поверхность), а вышеназванные средства измерений обычно снабжены мощным вычислительным аппаратом и компьютерными средствами. Различия в величинах отклонений, измеренных относительно прилегающей и средней поверхностей, практически не превышают 5 – 10%.
|
|
|
Допуском формы называется наибольшее допускаемое значение отклонения формы. Требования, определяемые допуском формы, геометрически поясняются понятием о поле допуска формы. Поле допуска формы – это область в пространстве или на плоскости, внутри которой должны находиться все точки реальной поверхности или реального профиля в пределах нормируемого участка.
Примечание: Следует помнить, что если к поверхности не предъявлено требование, ограничивающее отклонение формы, то в этом случае
допуск формы включен в допуск размера, причем 
= 1/2, =1/2; =1/2; = , где

- допуск линейного размера между двумя поверхностями, отклонение от плоскостности одной из которых рассматривается;
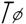 - допуск диаметрального размера цилиндрической поверхности.
- допуск диаметрального размера цилиндрической поверхности.
Схемы измерений, рассмотренные в данной работе, соответствуют ГОСТ 28187-89 «Общие требования к методам измерений отклонений формы и расположения поверхностей». Другие варианты схем измерения и более развернутые определения отклонений рассмотрены в [2].
I. Отклонение от прямолинейности  .
.
Отклонение от прямолинейности нормируется у плоских поверхностей, для которых важна форма в заданном направлении [4, Приложение 1]. Например, это характерно для направляющих станков или приборов; осей тел вращения; узких плоских поверхностей планок играющих роль направляющих баз и т.д.
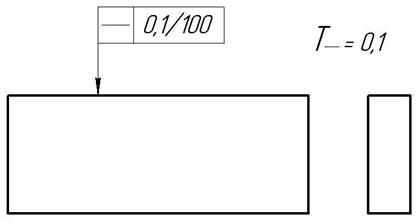
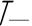 Задание №1. Измерить отклонение от прямолинейности сечения детали. Сравнить полученные результаты с допуском заданным на эскизе:
Задание №1. Измерить отклонение от прямолинейности сечения детали. Сравнить полученные результаты с допуском заданным на эскизе:
Оборудование:
1) Линейка лекальная ЛД ГОСТ 8026-75;
2) Набор щупов №1 (0,02; 0,03; 0,04; 0,05; 0,06; 0,07; 0,08; 0,09; 0,1) или набор щупов №2 (0,02; 0,03; 0,04; 0,05; 0,06; 0,07; 0,08; 0,09; 0,1; 0,15; 0,2; 0,25; 0,3; 0,35; 0,4; 0,45; 0,5);
3) Объект измерения: деталь с плоской поверхностью протяженной в одном направлении.
Методы измерения и контроля прямолинейности:
1) Измерение с помощью лекальной линейки;
|
|
|
 а) Метод “на просвет”: Лекальная линейка (Рис.2) прикладывается к измеряемому профилю по нормали к поверхности, так чтобы ребро касалось контролируемого профиля, материализуя прилегающую прямую (см. Приложение 1) Оценивается наибольшая ширина просвета между линейкой и деталью. Рассмотренный способ достаточно прост в реализации, нагляден, но позволяет лишь качественно оценить погрешность (выпуклость, вогнутость, волнистость и т.п.). Количественно определить величину по зазору без образцов просветов и достаточного опыта – невозможно, т.к. велика субъективная составляющая погрешности измерения.
а) Метод “на просвет”: Лекальная линейка (Рис.2) прикладывается к измеряемому профилю по нормали к поверхности, так чтобы ребро касалось контролируемого профиля, материализуя прилегающую прямую (см. Приложение 1) Оценивается наибольшая ширина просвета между линейкой и деталью. Рассмотренный способ достаточно прост в реализации, нагляден, но позволяет лишь качественно оценить погрешность (выпуклость, вогнутость, волнистость и т.п.). Количественно определить величину по зазору без образцов просветов и достаточного опыта – невозможно, т.к. велика субъективная составляющая погрешности измерения.
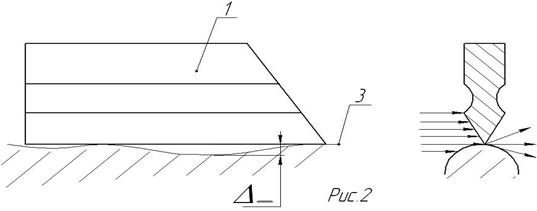
б) Метод с использованием набора щупов (Рис. 3а). Оценка наибольшего зазора между лекальной линейкой и профилем осуществляется с помощью набора щупов. Величина отклонения от прямолинейности считается равной размеру щупа наибольшей толщины, который проходит в зазор. К достоинствам метода можно отнести значительно бóльшую объективность результатов измерений, при сохранении простоты и доступности.
Недостатками этого метода являются:
- невозможность измерения отклонений менее минимальной толщины щупа;
- на результат влияет шероховатость измеряемой поверхности и достаточно большие размеры сечения щупа (см. Рис. 3 б)
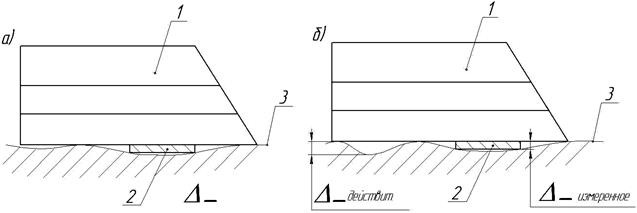
Рис.3.
Кроме рассмотренных, существует большое число различных методов измерения отклонения от прямолинейности, вот некоторые из них [2]:
- измерение различными оптоэлектронными устройствами;
- измерение изменений наклонов отдельных участков профиля;
- измерение на координатно-измерительной машине (КИМ);
- лазерное сканирование и др.
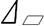 II. Отклонение от плоскостности.
II. Отклонение от плоскостности.
Отклонение от плоскостности [4, Приложение 1] обычно нормируется если:
1) Плоская поверхность является установочной базой (конструкторской, технологической или измерительной) и ее форма существенно влияет на точность базирования изделия.
Например:
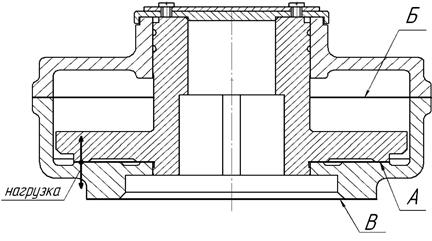
- плоскости основания корпусов редукторов (Рис.4, поверхность В);
- торцы фланцевых и закладных крышек, базирующие подшипники;
 - поверхности станочных и контрольных приспособлений (плиты, основания стоек и штативов и т.д.).
- поверхности станочных и контрольных приспособлений (плиты, основания стоек и штативов и т.д.).
|
|
|
Рис. 4. Узел колеса спироидного редуктора.
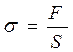 2) Плоская поверхность воспринимает значительные нагрузки и для уменьшения контактных напряжений площадь сопряжения должна быть максимально возможной, учитывая что
2) Плоская поверхность воспринимает значительные нагрузки и для уменьшения контактных напряжений площадь сопряжения должна быть максимально возможной, учитывая что
Например:
- плоские поверхности колеса и корпуса спироидного редуктора, воспринимающие нормальные и тангенциальные нагрузки от зубчатого зацепления (Рис. 4, поверхность А).
3) Плоская поверхность, влияет на герметичность машины.
Например:
-плоскость разъема корпуса (Рис. 4, поверхность Б);
-торцы отверстий в корпусе под установку крышек;
-торцы крышек и фланцев, соприкасающиеся с корпусом.
4) Плоскость предназначена для правильного отражения и преломления световых потоков (зеркала, призмы и т.п.)
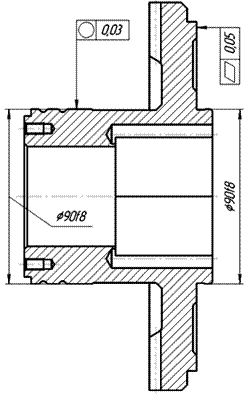 Задание №2.1. Измерить отклонение от плоскостности торцовой поверхности колеса. Сравнить полученные результаты измерений с заданными требованиями. Фрагмент рабочего чертежа детали представлен на рис.5.
Задание №2.1. Измерить отклонение от плоскостности торцовой поверхности колеса. Сравнить полученные результаты измерений с заданными требованиями. Фрагмент рабочего чертежа детали представлен на рис.5.
Рис.5. Фрагмент чертежа детали «колесо спироидное».
Оборудование (см. Рис. 6 и 7):
1) Плита поверочная чугунная
400х400 ГОСТ 10905-86;
2) Плоскопараллельные концевые меры длины КМД-100 (4 шт.) ГОСТ 9038-90;
3) Стойка индикаторная (или штатив);
4) Индикаторная головка 2ИГ ГОСТ 18833-73;
5) Планка настроечная с плоской поверхностью.
6) Объект измерения: колесо спироидное или фланец.
Порядок проведения измерений
1. Измеряемая плоскость колеса условно разделяется на 12 секторов примерно по 30° каждый и маркируется, как показано на Рис.6.
2. Колесо 6 тремя точками измеряемой поверхности расположенными примерно в 120° друг от друга (точки а, в, с) устанавливается на три опоры равной высоты - концевые меры длины 100 мм (КМ-100).
3. Проверив допустимость использования измерительной головки 4 (2ИГ) для контроля заданного отклонения (см. Приложение 4), установить ее на штатив 3.
4. Настроить индикаторную головку на “0” по КМ -100, как показано на рис.7.
5. Аккуратно перемещая штатив с индикатором за основание штатива по плите, не отрывая от ее поверхности, определить отклонения от настроенного размера в 9-ти свободных от КМ-100 точках торца колеса (см. рис. 6).
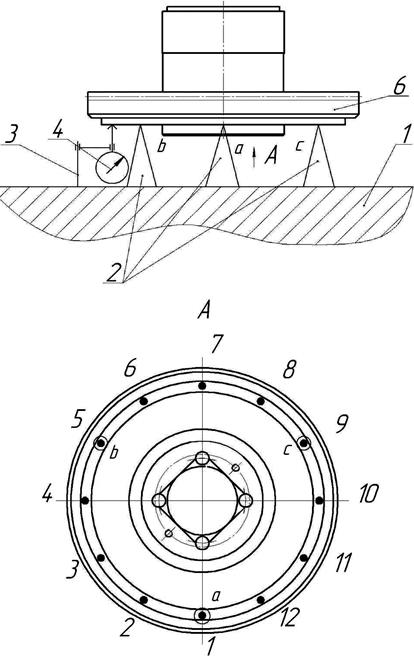
Рис.6. Схема измерения отклонения от плоскостности.

Рис.7. Настройка индикатора на «0».
6. Результаты с указанием знака внести в таблицу 1:
Таблица 1
| № точки | Показание индикатора, мкм | № точки | Показание индикатора, мкм | № точки | Показание индикатора, мкм |
| 1 ”a” | 5 “b” | 9 “c” | |||
|
|
|
7. Выбрать 3 точки, наиболее удаленные друг от друга и при этом ближайшие к плите (знак“+” или “-” зависит от разметки шкалы индикаторной головки). Это наиболее вероятные точки, принадлежащие прилегающей плоскости (см. Приложение 1), так как выступают относительно других.
8. Передвинуть опоры (концевые меры длины) в найденные точки (см. п.7), которые теперь будут называться “a”, “b”, “c”.
9. Повторить измерение в 9-ти оставшихся точках (см. п. 4 и.5).
10. Результаты с указанием знака внести в таблицу 2.
Таблица 2
| № точки | Показание индикатора, мкм | № точки | Показание индикатора, мкм | № точки | Показание индикатора, мкм |
Примечание: 1) Если прилегающая плоскость найдена правильно, вернее плоскость проходящая через новые точки “a”, “b”, “c” близка к прилегающей, тогда во всех остальных точках показания индикатора будут с одинаковым знаком (“+” или “-” в зависимости от особенностей шкалы индикаторной головки).
2) Если значения в таблице 2 имеют разный знак, для более точного определения прилегающей плоскости повторить пункты 7,8,9 еще раз.
11. 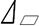 Определить =/
Определить =/ 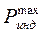 /, где
/, где 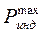 - максимальное показание индикатора из таблицы 2, соответствующее наибольшему отклонению точек торцовой поверхности колеса относительно прилегающей плоскости, найденной в п.7.
- максимальное показание индикатора из таблицы 2, соответствующее наибольшему отклонению точек торцовой поверхности колеса относительно прилегающей плоскости, найденной в п.7.
12. 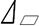 Сравнить с допуском формы
Сравнить с допуском формы  и сделать вывод.
и сделать вывод.
Кроме рассмотренного существует множество других способов измерения и контроля отклонения от плоскостности [2]. Некоторые из них приведены ниже:
-Контроль отклонения от плоскостности сравнением с лекальной плитой “по краске”: на эталонную плиту наносится тонкий слой (до 5-10 мкм.) специальной краски, измеряемая плоская поверхность прикладывается к эталонной. Затем по следам (их размерам, количеству и расположению) оценивается отклонение от плоскостности.
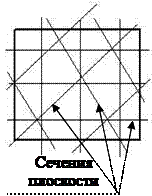
 -Измерение небольших точных светоотражающих поверхностей с шероховатостью не более Ra 0.08 с помощью плоскопараллельных стекол (ПИ60, ПИ80, ПИ100, ПИ120). Метод основан на использовании дисперсии света в тонких пленках (так называемых «интерференционных колец Ньютона»). Можно принять что один полный «сектр» соответствует зазору в λ красн ≈ 0,6 мкм.
-Измерение небольших точных светоотражающих поверхностей с шероховатостью не более Ra 0.08 с помощью плоскопараллельных стекол (ПИ60, ПИ80, ПИ100, ПИ120). Метод основан на использовании дисперсии света в тонких пленках (так называемых «интерференционных колец Ньютона»). Можно принять что один полный «сектр» соответствует зазору в λ красн ≈ 0,6 мкм.
- В неответственных случаях допустимо контроль отклонения от плоскостности заменять контролем отклонения от прямолинейности в нескольких сечениях (см. рис справа).
- Измерение с помощью КИМ;
- Измерение с помощью лазерного сканирования;
и т.д.
Задание №2.2. Измерить с помощью плоскопараллельного стекла отклонение от плоскостности небольшой точной поверхности.
Оборудование: 1) Плоскопараллельное стекло (ПИ80 или ПИ100);
2) Объект измерения.
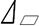 Отклонение определяется по формуле: = n · λкрасн ,,
Отклонение определяется по формуле: = n · λкрасн ,,
где N – количество видимых красных полос «спектров»,
λкрасн – длина волны красного цвета (≈600 нм).
III. Отклонение от цилиндричности 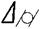 .
.
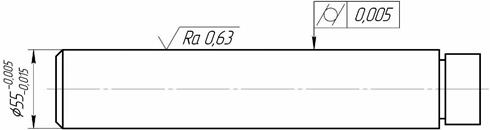 Задание №3.1. Измерить отклонение от цилиндричности (определение см. [4, Приложение 1]) поверхности измерительной оправки, используя схему на рис.12. Сравнить полученные результаты с допуском заданным на эскизе:
Задание №3.1. Измерить отклонение от цилиндричности (определение см. [4, Приложение 1]) поверхности измерительной оправки, используя схему на рис.12. Сравнить полученные результаты с допуском заданным на эскизе:
Оборудование:
1) Плита поверочная чугунная 400х400 ГОСТ 10905-86;
2) Стойка индикаторная (или штатив);
3) Индикаторные головки 1ИГ, 1МИГ и др.;
4) Оправка измерительная.
Известно, что величина отклонения от цилиндричности (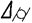 ) нормируется относительно прилегающего цилиндра. Следовательно, при контроле для выполнения принципа совмещения измерительных и конструкторских баз необходимо каким-либо образом материализовать прилегающий цилиндр (см. примечания в Приложении 1), что требует применения сложных средств и схем измерений, например использование КИМ и др. [2]. Так как в настоящее время такие средства и схемы еще не получили повсеместного распространения на производстве, то чаще всего на практике контроль отклонения
) нормируется относительно прилегающего цилиндра. Следовательно, при контроле для выполнения принципа совмещения измерительных и конструкторских баз необходимо каким-либо образом материализовать прилегающий цилиндр (см. примечания в Приложении 1), что требует применения сложных средств и схем измерений, например использование КИМ и др. [2]. Так как в настоящее время такие средства и схемы еще не получили повсеместного распространения на производстве, то чаще всего на практике контроль отклонения 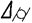 заменяют контролем отклонений от круглости
заменяют контролем отклонений от круглости  и профиля продольного сечения
и профиля продольного сечения 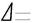 , учитывая, что между ними есть связь.
, учитывая, что между ними есть связь.
 ≈
≈ 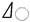 +
+ 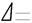 , или точнее
, или точнее 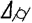 2 ≈
2 ≈ 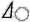 2 +
2 +  2 (1)
2 (1)
При измерении, материализовать прилегающую окружность и прилегающий профиль цилиндра (см. примечание к Приложению 1) значительно легче из-за простоты их геометрической формы. Кроме того, существует множество приближенных методов контроля частных случаев вышеназванных отклонений без использования прилегающих профилей, так называемые «двухточечные» и «трехточечные» схемы.
В данной лабораторной работе рассматриваются некоторые из приближенных методов определения  и
и 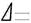 , которые в большинстве случаев обеспечивают необходимую точность измерений, но все же неизбежно содержат методическую погрешность, обусловленную несовпадением измерительной и конструкторской баз.
, которые в большинстве случаев обеспечивают необходимую точность измерений, но все же неизбежно содержат методическую погрешность, обусловленную несовпадением измерительной и конструкторской баз.
Частными случаями отклонений от круглости являются овальность и огранка.
Овальность (рис.8) — отклонение от круглости, при котором реальный профиль представляет собой овалообразную фигуру, наибольший в наименьший диаметры которой находится во взаимно перпендикулярных направлениях.
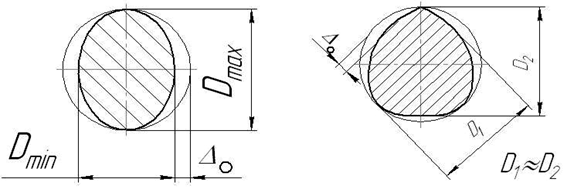 Огранка (рис.9) — отклонение от круглости, при котором реальный профиль представляет собой многогранную фигуру. Виды огранки отличаются количеством граней. В частности, огранка с нечетным числом граней характеризуется тем, что диаметры профиля поперечного сечения во всех направлениях почти одинаковы.
Огранка (рис.9) — отклонение от круглости, при котором реальный профиль представляет собой многогранную фигуру. Виды огранки отличаются количеством граней. В частности, огранка с нечетным числом граней характеризуется тем, что диаметры профиля поперечного сечения во всех направлениях почти одинаковы.
Рис. 8 Рис.9
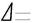
 Самым простым, но и наименее точным способом измерения формы является 2-х точечная схема измерений и
Самым простым, но и наименее точным способом измерения формы является 2-х точечная схема измерений и
 При овальности (рис. 8) отклонение от круглости можно определить простым измерением диаметров в 2-х сечениях под углом 90º (Рис. 10.а).
При овальности (рис. 8) отклонение от круглости можно определить простым измерением диаметров в 2-х сечениях под углом 90º (Рис. 10.а).
(2)
В случае других вариантов отклонений от круглости с четным количеством граней эта зависимость принимает вид (3), а величина  при 2-х точечной схеме измерения определяется в сечениях указанных на рис.10. б и 10.в.
при 2-х точечной схеме измерения определяется в сечениях указанных на рис.10. б и 10.в.
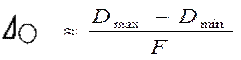
(3), где F- коэффициент (рис.10.б и в), учитывающий количество и угол между направлениями измерений диаметров.
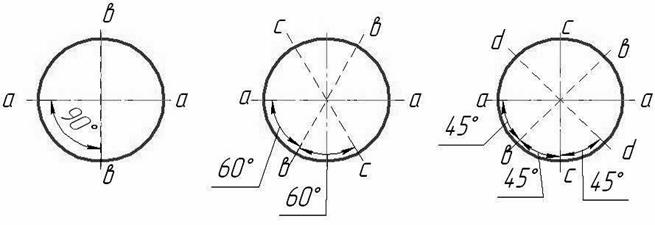 а) в 2-х направлениях; б) в 3-х направлениях (F=1,6);
а) в 2-х направлениях; б) в 3-х направлениях (F=1,6);
в) в 4-х направлениях (F=1,7);
Рис. 10. Измерение отклонения от круглости через разницу диаметров.
Частные случаи отклонения профиля продольного сечения показаны на рис.11.
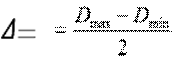 Величину отклонения для них так же можно определить по разнице диаметров в некоторых сечениях, измеренных в 2-х точечной схеме.
Величину отклонения для них так же можно определить по разнице диаметров в некоторых сечениях, измеренных в 2-х точечной схеме.
(4)
Конусообразность - отклонение профиля продольного сечения, при котором образующие прямолинейны, но не параллельны (рис.11, а).
Бочкообразность - отклонение профиля продольного сечения, при котором образующие непрямолинейны и диаметры увеличиваются от краев к середине сечения (рис.11, б).
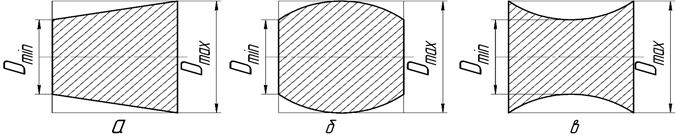 Седлообразность - отклонение профиля продольного сечения, при котором образующие непрямолинейны и диаметры уменьшаются от краев к середине сечения (рис.11, в).
Седлообразность - отклонение профиля продольного сечения, при котором образующие непрямолинейны и диаметры уменьшаются от краев к середине сечения (рис.11, в).
Рис. 11
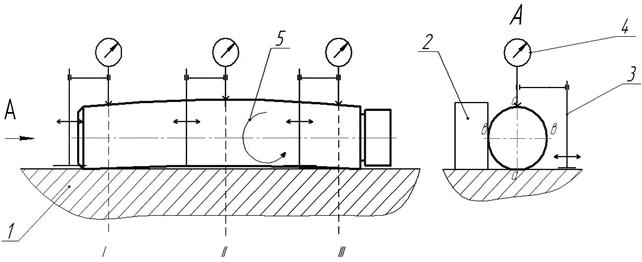
Рис.12
Если же отклонения от круглости и профиля продольного сечения не относятся ни к одному из рассмотренных частных случаев или их характер заранее не известен, то измерение можно провести согласно рис.12, на котором показана реализация той же 2-х точечной схемы.
Плоскость контрольной плиты 1, касательная к поверхности объекта измерения 5, материализует нижнюю образующую прилегающего профиля. Штатив 3 с установленной в нем индикаторной головкой 4 перемещается по поверхности плиты так, чтобы в каждом из сечений I-а, I-b, II-a, II-b, III-a и III-b определить по шкале индикатора 4 разницу расстояний точек верхней образующей оправки от плиты. Измерения а-а и b-b необходимо проводить в 2-х взаимно перпендикулярных сечениях. По формулам (5) и (6) определяются искомые отклонения.
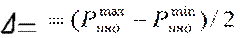 | |||
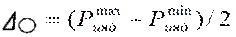 | |||
(5) и (6),
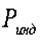
 Где - показание измерительного устройства, определяющего колебание расстояния от базовой плоскости до точек верхней образующей объекта. Для формулы (4) max и min значения следует выбирать в парах (I-а и I-b),(II-a и II-b), (III-a и III-b), таким образом, получится 3 величины
Где - показание измерительного устройства, определяющего колебание расстояния от базовой плоскости до точек верхней образующей объекта. Для формулы (4) max и min значения следует выбирать в парах (I-а и I-b),(II-a и II-b), (III-a и III-b), таким образом, получится 3 величины 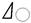 . Для формулы (5) max и min значения следует выбирать из 3-х значений (I-а, II-a,III-a) и (I-b, II-b,III-b), таким образом, получится 2 величины.
. Для формулы (5) max и min значения следует выбирать из 3-х значений (I-а, II-a,III-a) и (I-b, II-b,III-b), таким образом, получится 2 величины.
Вычислить величину  , квадратично сложив максимальные
, квадратично сложив максимальные  и
и  по ф.(1).
по ф.(1).
В качестве индикаторной головки в схеме на рис. 12 могут быть использованы различные средства измерений: индикаторные головки 1ИГ, 2ИГ или 1МИГ (см. Приложение 2), выбор которых зависит от допустимой погрешности измерений (см Приложение 4). В качестве контрольной плиты для измерения небольших деталей можно использовать плоские столики измерительных приборов (оптиметров, микрокаторов, вертикальных длинномеров и т.п.), для измерения крупных объектов больше подойдут поверочные плиты разных размеров.
Задание №3.2. Измерить отклонение от круглости короткой цилиндрической поверхности колеса (рис. 5) или фланца используя трехточечную схему измерения. Сравнить полученные результаты с допуском 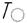 =0,03мм.
=0,03мм.
Оборудование: 1) Плита поверочная чугунная 400х400 ГОСТ 10905-86;
2) Стойка индикаторная (или штатив);
3) Индикаторные головки 1ИГ, 1МИГ, ИЧ10 и др.;
4) Комплект призм измерительных.
Трехточечная схема измеренияотклонений от круглости является методически более правильной по сравнению с двухточечной. Кроме того, в случае нечетного количества граней на поверхности, 2-х точечную схему использовать нерационально (см. рис. 8 и 9). Примерыприменениятрехточечных схем измерения отклонений поверхностей валов рассмотрены ниже (рис. 13 и 14).
1) Измерение вала с базированием в призме.
Различают симметричную схему измерения, когда измерительный наконечник располагается по биссектрисе угла α (Рис.13, а) и несимметричную схему, когда измерительный наконечник располагается под углом β к биссектрисе (Рис.13, б).
Измеряемый вал устанавливают в призме и вращают, определяя наибольшее изменение показаний индикаторной головки за один оборот объекта. Отклонение от круглости  при этом будет вычисляться по формуле:
при этом будет вычисляться по формуле:
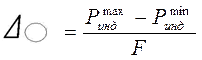 (7), где F - коэффициент, который зависит от количества неровностей на периметре детали, угла α или комбинации углов α и β (см. таблицы 3 и 4).
(7), где F - коэффициент, который зависит от количества неровностей на периметре детали, угла α или комбинации углов α и β (см. таблицы 3 и 4).

а) симметричная схема б) несимметричная схема
Рис.13. Измерение отклонения от круглости вала в призме:
(1 – измеряемая деталь; 2 – призма; 3 – измерительная головка; 4 – штатив).
2) Измерения вала с применением седлообразной призмы (наездника). Рис.14
 Базирование вала 1 может осуществляться по-разному: в центрах 4, в патроне или в призмах, но индикаторное устройство 3 устанавливается в накладной призме 2 (наезднике).
Базирование вала 1 может осуществляться по-разному: в центрах 4, в патроне или в призмах, но индикаторное устройство 3 устанавливается в накладной призме 2 (наезднике).
Рис.14. Измерение вала с применением седлообразной призмы.
Вал имеет возможность совершать вращательное движение относительно индикатора установленного в наезднике. На основании разницы показаний индикаторной головки 3 по формуле (6) можно вычислить отклонение. Коэффициент F см. в таблице 5.
Коэффициенты при вычислении отклонения от круглости при симметричной 3-х точечной схеме измерений (рис. 13.а)
Таблица 3
| Количество неровностей на периметре n | Поправочный коэффициент 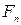 для случая для случая
| |||
| α = 180º | α = 90º | α = 60º | α = 120º | |
| 1,38 1,38 * 2,24 | 1,00 2,00 0,41 2,00 | * 3,00 * * | 1,58 1,00 0,42 2,00 | |
| * 1,38 1,38 * 2,24 | 1,00 * 2,41 * 1,00 | 3,00 * * 3,00 * | * 2,00 0,42 1,00 1,58 |
Коэффициенты при вычислении отклонения от круглости при несимметричной 3-х точечной схеме измерений (Рис. 13.б)
Таблица 4
| Количество неровностей на периметре n | Поправочный коэффициент 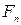 для случая для случая
| ||
| α = 120º β = 60º | α = 60º β = 30º | α = 120º β = 10º | |
| 2,38 2,00 1,01 2,00 | 1,41 2,00 1,41 2,00 | 1,64 0,88 0,96 1,73 | |
| 0,42 2,00 1,01 2,00 2,38 | 0,73 2,00 1,41 2,00 1,41 | 1,08 1,73 0,79 1,35 0,79 |
Коэффициенты при вычислении отклонения от круглости при симметричной 3-х точечной схеме измерений с наездником (рис. 14)
Таблица 5
| Количество неровностей на периметре n | Поправочный коэффициент 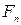 для случая для случая
| Количество неровностей на периметре n | Поправочный коэффициент 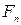 для случая для случая
| ||||
| α = 72º | α = 90º | α = 120º | α = 72º | α = 90º | α = 120º | ||
| 1,53 | 1,0 | 0,42 | 2,0 | * | 1,0 | ||
| 2,62 | 2,0 | 1,0 | 2,7 | 1,0 | 0,42 | ||
| 2,38 | 2,41 | 1,58 | 2,0 | 2,0 | * | ||
| 1,0 | 2,0 | 2,0 | 0,47 | 2,41 | * | ||
| 0,38 | 1,0 | 2,15 | 0,62 | 2,0 | * | ||
| 0,62 | * | 2,0 | 0,38 | 1,0 | 0,42 | ||
| 0,47 | 0,41 | 1,58 | 1,0 | * | 1,0 |
Примечание: Для случаев отмеченных * отсутствует изменение показаний измерительной головки.
Кроме рассмотренных выше схем, для определения величины отклонения от круглости применяются специальные средства тем или иным образом материализующие прилегающую окружность (кругломеры). При этом измерительной базой становится именно прилегающая окружность, что полностью соответствует стандартному описанию искомой погрешности. Таким образом, методическая составляющая погрешности измерений становится практически равной нулю, что существенно увеличивает точность измерений, необходимую в особо ответственных случаях.
Рис. 15. Измерение с применением образца круглости.
(1 – измеряемая деталь; 2 – образец круглости «калибр-кольцо», материализующий прилегающую окружность; 3 – измерительная головка.)
 Схема измерения показана на рис.15. Измеряемая деталь сопрягается с образцовой по форме деталью (кольцом или пробкой), которая в ограниченном диапазоне диаметров материализует прилегающую окружность. Измерительной головкой, закрепленной неподвижно на образцовой детали, регистрируется максимальная разность показаний за один оборот измеряемой детали относительно образцовой. Для более полной компенсации действительных отклонений диаметра деталей применяют образцовые детали, регулируемые по диаметру, либо набор различных по диаметру образцовых деталей.
Схема измерения показана на рис.15. Измеряемая деталь сопрягается с образцовой по форме деталью (кольцом или пробкой), которая в ограниченном диапазоне диаметров материализует прилегающую окружность. Измерительной головкой, закрепленной неподвижно на образцовой детали, регистрируется максимальная разность показаний за один оборот измеряемой детали относительно образцовой. Для более полной компенсации действительных отклонений диаметра деталей применяют образцовые детали, регулируемые по диаметру, либо набор различных по диаметру образцовых деталей.
|
|
|


