Основное уравнение турбомашин Эйлера

Движение жидкости в каналах рабочего колеса центробежного насоса

Движение реальной жидкости в межлопаточных каналах рабочего колеса представляет собой весьма сложный гидромеханический процесс. Поэтому до настоящего времени уравнения движения получить чисто теоретическим путем не удается. Теоретические уравнения движения жидкости в межлопаточных каналах динамических гидромашин (лопаточных насосов и гидротурбин) получены Л.Эйлером при следующих двух допущениях:

1 Жидкость идеальная, т.е. гидравлические сопротивления не учитываются.

2 Жидкость движется в виде бесконечного числа элементарных струек, строго повторяющих форму лопаток.

Эти допущения облегчают теоретическое исследование движения жидкости в лопаточных системах, но в дальнейшем требуют внесения существенных поправок на основании экспериментальных исследований.

Движение каждой частицы жидкости потока в рабочем колесе является сложным, абсолютная скорость, которой складывается из переносной и относительной скоростей. Скорость переносного движения - это линейная скорость вращательного движения точки рабочего колеса, где в данный момент находится частица жидкости. Эта скорость направлена по касательной к окружности, на которой находится частица. Относительная скорость – это скорость перемещения частицы относительно лопатки колеса: вектор относительной скорости направлен по касательной к лопатке.

Абсолютная скорость определяется как векторная сумма:

.

Параллелограммы скоростей на входе в межлопаточные каналы и выходе из них показаны на рис

Все величины на входе обозначаются с индексом - «1», а на выходе – «2».

Если угловая скорость вращения рабочего колеса ω, т.е. окружные линейные скорости будут равны:

Векторы относительных скоростей W₁ и W₂ направлены по касательной к стенкам лопаток рабочего колеса.

Углы, определяющие форму лопатки рабочего колеса, обозначаются β₁ и β₂ - это углы между направлением относительной скорости W и в обратном направлении окружной скорости (-U).

Углы между направлением абсолютной скорости С и окружной скорости U обозначаются α₁ и α ₂ (рисунок 3.10).

Из уравнения неразрывности потока жидкости, протекающего через рабочее колесо, следует

,

где C_1r и C_2r - радиальные составляющие абсолютных скоростей на входе и выходе, а площади сечения и представляют собой поверхности вращения с образующей, нормальной к радикальной скорости. Обычно вместо параллелограммов скоростей строят треугольники скоростей (рисунок 3.11).

Площади сечений и F₂

равны:

на входе: ,

на выходе: ,

где и – соответственно диаметры на входе в межлопаточные каналы и выходе из них; и 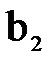– ширина лопатки (канала); 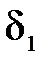и – толщина лопаток, z - число лопаток.

– представляет собой идеальную подачу рабочего колеса центробежного насоса.

Основное уравнение турбомашин Эйлера

Воспользуемся теорией об изменении момента количества движения и сформулируем ее для потока жидкости в рабочем колесе межлопаточных каналов.

Изменение момента количества движения потока времени, где 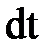относительно оси вращения рабочего колеса равно импульсу момента всех внешних сил, действующих на поток, относительно той же оси, т.е. импульсу крутящего момента на валу насоса.

Пусть жидкость массой m движется с абсолютной скоростью С, тогда ко­личество движения этой массы составит вектор , направле­ние которого совпадает с направ­лением вектора скорости С. Момент количества движения массы относительно оси вращен­ия рабочего колеса, как это показано на рисунке составит:

на входе в лопастное колесо

,

на выходе из колеса ,

где m - масса жидкости, вошедшая в межлопаточные каналы и вышедшая из них за время dt, которую можно выразить через объемный расход и плотность :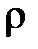

,где и - плечи, представляющие собой перпендикуляры, опущенные из центра вращения колеса на направление вектора абсолютной скорости.

Плечи и можно заменить соответственно через радиусы входа и выхода жидкости из рабочего колеса:

, .

Изменение момента количество движения равно

Подставляя значения M₁ и M₂, получим

Итак, левая часть исходного уравнения равна .

Правая часть исходного уравнения представляет собой момент внешних сил, действующих на поток относительно оси вращения рабочего колеса, т.е. крутящий момент на валу насоса.

Момент умножим на угловую скорость вращения колеса - это составит мощность на валу насоса, т.е. потребляемую мощность: .

Приращение энергии потока жидкости в рабочем колесе, т.е. полезная мощность насоса: ,

где - теоретический напор при бесконечном числе лопаток.В данном случае ,т.к. жидкость идеальная и вся потребляемая мощность переходит в полезную. Из условия вытекает:

, т.к. , то

.

Полученное уравнение называют уравнением Эйлера для турбомашин.

Если вход жидкости в рабочее колесо насоса радиальный ( =90°), как это имеет место у большинства центробежных насосов (закрутка потока отсутствует), т.е. , то уравнение Эйлера записывается в следующем виде:

.

Поделиться:

Воспользуйтесь поиском по сайту: